Язык логики высказываний
Логика высказываний была построена в 1879 г. немецким учёным Фреге, хотя её предшественниками следует считать представителей мегарской школы, возникшей в 4 в. до н. э. в рамках древнегреческой философии. Вслед за мегариками основные её идеи разрабатывались стоиками, школа которых существовала ещё во времена Римской империи. В средние века им трудно было конкурировать с логикой Аристотеля, опиравшейся на поддержку католической церкви. Поэтому логика высказываний стала привлекать внимание исследователей только с 17 в., когда на волне нарождавшегося капитализма началось интенсивное развитие математики и естествознания. Но потребовалось ещё два столетия, чтобы она превратилась в самостоятельную область логических исследований, специфика которой находит своё выражение в её языке и используемых методах.
Язык логики высказываний характеризуется словарём, т. е. перечнем исходных символов, а также понятием осмысленного выражения (или формулы). Словарь языка логики высказываний включает в себя бесконечное множество пропозициональных переменных
p, q, r, … ,
принимающих значения на множестве высказываний, и особые символы для пропозициональных связок: ~ – отрицание, 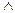 – конъюнкция,
– конъюнкция, 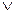 – дизъюнкция и
– дизъюнкция и 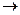 – импликация. В качестве технических выражений используются скобки, которые играют роль знаков препинания обычного языка.
– импликация. В качестве технических выражений используются скобки, которые играют роль знаков препинания обычного языка.
Для того чтобы проиллюстрировать значение скобок в языке логики высказываний, обратимся к следующему примеру. Предположим, что нам надо записать символически высказывание «Я пойду домой или останусь здесь и буду её ждать». Пытаясь уяснить смысл этого высказывания, мы приходим к выводу, что оно допускает двоякое истолкование. Первое из этих истолкований заключается в том, что мы имеем дело с дизъюнкцией, дизъюнктами которой являются высказывания «Я пойду домой» (p) и «Я останусь здесь и буду её ждать» (q 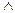 r). Второе истолкование сформулированного нами высказывания заключается в том, что мы имеем дело не с дизъюнкцией, а с конъюнкцией, конъюнктами которой являются высказывания «Я пойду домой или останусь здесь» (p
r). Второе истолкование сформулированного нами высказывания заключается в том, что мы имеем дело не с дизъюнкцией, а с конъюнкцией, конъюнктами которой являются высказывания «Я пойду домой или останусь здесь» (p 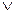 q) и «Я буду её ждать» (r). Как видно, различие между двумя истолкованиями нашего высказывания существенно. Однако без использования скобок его выразить просто невозможно, поскольку в обоих случаях мы получаем одну и ту же формулу: p
q) и «Я буду её ждать» (r). Как видно, различие между двумя истолкованиями нашего высказывания существенно. Однако без использования скобок его выразить просто невозможно, поскольку в обоих случаях мы получаем одну и ту же формулу: p 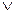 q
q 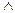 r. Расставив скобки, мы получим уже две различные формулы:
r. Расставив скобки, мы получим уже две различные формулы:
p 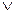 (q
(q 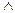 r)
r)
и
(p 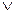 q)
q) 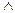 r.
r.
Таким образом, скобки позволяют нам более точно выразить тот смысл, который мы вкладываем в выражения языка логики высказываний.
Понятие формулы в логике высказываний определяется следующим образом:
· пропозициональная переменная является формулой;
· если A – формула, то ~ A также является формулой;
· если A и B – формулы, то A 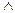 B, A
B, A 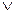 B и A
B и A 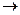 B также являются формулами.
B также являются формулами.
В отличие от пропозициональных переменных p, q, r, … , обозначающих конкретные высказывания, буквы A и B в определении формулы логики высказываний обозначают произвольные высказывания. Так, частным случаем схемы A 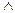 B является не только высказывание p
B является не только высказывание p 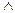 q, но и высказывания p
q, но и высказывания p 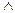 ~ q, ~ p
~ q, ~ p 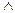 q, (p
q, (p 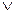 q)
q) 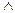 (q
(q 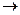 r) и т. д. Все эти высказывания объединяет то, что главной связкой в них является конъюнкция, т. е. при их построении она применялась последней.
r) и т. д. Все эти высказывания объединяет то, что главной связкой в них является конъюнкция, т. е. при их построении она применялась последней.
Формулы логики высказываний, образованные из переменных и связок с возможным использованием скобок, обозначают высказывания, которым в естественном языке соответствуют предложения как их материальная оболочка. Так, если переменной p придать значение «Народ недоволен», переменной q – значение «Растёт инфляция», а переменной r – значение «Жизненный уровень падает», то формула p 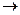 (q
(q 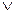 r) будет обозначать высказывание «Если народ недоволен, то растёт инфляция или жизненный уровень падает», формула (q
r) будет обозначать высказывание «Если народ недоволен, то растёт инфляция или жизненный уровень падает», формула (q 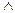 r)
r) 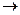 p – высказывание «Если растёт инфляция и жизненный уровень падает, то народ недоволен», формула ~ q
p – высказывание «Если растёт инфляция и жизненный уровень падает, то народ недоволен», формула ~ q 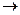 ~ p – высказывание «Если инфляция не растёт, то неверно, что народ недоволен» и т. д. Придавая переменным p, q и r иные значения (например, p – «Правительство проводит правильный экономический курс», q – «Рубль укрепляется», а r – «Инфляция падает»), мы получим другие переводы этих формул на обычный язык.
~ p – высказывание «Если инфляция не растёт, то неверно, что народ недоволен» и т. д. Придавая переменным p, q и r иные значения (например, p – «Правительство проводит правильный экономический курс», q – «Рубль укрепляется», а r – «Инфляция падает»), мы получим другие переводы этих формул на обычный язык.
Дата добавления: 2020-12-11; просмотров: 730;











