Истинностные таблицы
Логика высказываний (или пропозициональная логика) представляет собой раздел логики, в котором изучаются свойства пропозициональных связок, служащих для образования сложных высказываний из простых. Часто правильность наших умозаключений зависит от того, как мы понимаем пропозициональные связки. При этом нас не интересует структура простых высказываний (т. е. являются ли они, например, общеутвердительными или частноотрицательными), а интересует только то, как из них образуются сложные высказывания. Поэтому мы и называем простые высказывания атомарными, обозначая их отдельными буквами. Как известно, греческие философы Левкипп, Демокрит и их последователи полагали, что существуют неделимые частицы, которые они называли атомами и рассматривали как основу всего существующего. В отличие от древнегреческих атомистов, в логике не утверждают существование бесструктурных высказываний, а просто в некоторых случаях считают возможным отвлечься от их структуры. С одним из таких случаев мы сталкиваемся, например, в умозаключении
Если инфляция растёт, то уровень жизни людей падает. Инфляция растёт. Следовательно, уровень жизни людей падает,
для обоснования заключения которого необходимо знать, истинны ли его посылки и как понимается выражение «если, то» (импликация).
Имеются различные способы построения логики высказываний: табличный, аксиоматический и др. При табличном построении логики высказываний, которое мы выбираем как более приемлемое с интуитивной точки зрения, исходят из двух предпосылок, называемых семантическими. Вообще существует три уровня изучения языка – синтаксис, семантика и прагматика. Синтаксис изучает отношения между выражениями языка, отвлекаясь от описываемой им реальности, а также от его использователей. Центральное положение занимают в нём понятия аксиомы, теоремы, доказательства и т. д. Что касается семантики, то она изучает отношения между выражениями языка, с одной стороны, и описываемой им реальностью – с другой, но отвлекается от его использователей. Типично семантическими являются понятия значения, истины, лжи и др. Наконец, прагматика не только изучает отношения между выражениями языка и описываемой им реальностью, но и принимает во внимание его использователей, в качестве которых могут выступать отдельные люди или их группы. Центральное положение занимают в ней понятия знания, мнения, убеждения и т. д. Прагматический аспект изучения языка очень важен, но ещё не так детально разработан в науке, как семантический, которого мы и будем придерживаться в данной главе[1].
Первая семантическая предпосылка логики высказываний заключается в том, что каждое высказывание может быть либо истинным, либо ложным, но не тем и другим одновременно. Истина и ложь называются истинностными значениями (или просто значениями) высказываний. Первую обозначают обычно с помощью единицы (1), а вторую – с помощью нуля (0). Если в логике принимается два истинностных значения, то она называется двузначной (или классической) логикой. Помимо двузначной, существует многозначная (или неклассическая) логика, в которой принимается три или более истинностных значений. Корни многозначной логики можно обнаружить у Аристотеля, который для высказываний о случайных будущих событиях (например, «Завтра будет морское сражение») допускал третье значение – «неопределённо». Действительно, случайное событие может в будущем произойти, а может и не произойти. Поэтому высказывание об этом событии, сделанное сегодня, не может быть истинным или ложным, а может быть только неопределённым. Тем не менее вопрос о практическом использовании многозначной логики остаётся открытым, а сама она требует дальнейших исследований.
Вторая семантическая предпосылка логики высказываний заключается в том, что истинностные значения сложных высказываний зависят от истинностных значений входящих в них простых высказываний, а также от смысла пропозициональных связок. Установление смысла пропозициональных связок сводится к формулировке условий истинности для различных типов сложных высказываний, т. е. для отрицания, конъюнкции, дизъюнкции и т. д. Такие условия формулируются обычно с помощью истинностных таблиц, которые имеют преимущество наглядности по сравнению с другими способами определения пропозициональных связок. Несмотря на свою простоту, метод истинностных таблиц позволяет решать любые проблемы, возникающие в логике высказываний.
Истинностная таблица для отрицания включает в себя две строки, соответствующие возможным значениям некоторого высказывания A, к которому оно применяется:
| A | ~ A |
Как видно из этой таблицы, высказывание ~ A ложно, если A истинно, и истинно, если A ложно. Так, высказывание «Банк Америки не является американским банком» ложно, поскольку высказывание «Банк Америки является американским банком» истинно. С другой стороны, высказывание «Банк Америки не является российским банком» истинно, поскольку высказывание «Банк Америки является российским банком» ложно.
Истинностные таблицы для конъюнкции, дизъюнкции и импликации включают в себя уже не две, а четыре строки, поскольку мы должны учитывать в них все возможные комбинации значений двух высказываний A и B, к которым они применяются:
| A | B | A 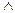 B B
| A 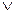 B B
| A 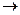 B B
|
Как видно из этих таблиц, конъюнкция истинна только тогда, когда все её конъюнкты истинны, а в остальных случаях она ложна. Дизъюнкция ложна только тогда, когда все её дизъюнкты ложны, а в остальных случаях она истинна. Импликация ложна только тогда, когда её антецедент истинен, а консеквент ложен, а в остальных случаях она истинна. Так, если высказывание «В Екатеринбурге проживает более одного миллиона человек» (p) истинно, а высказывание «Екатеринбург – столица России» (q) ложно, то высказывание «В Екатеринбурге проживает более одного миллиона человек и Екатеринбург – столица России» (p 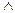 q) ложно, высказывание «В Екатеринбурге проживает более одного миллиона человек или Екатеринбург – столица России» (p
q) ложно, высказывание «В Екатеринбурге проживает более одного миллиона человек или Екатеринбург – столица России» (p 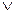 q) истинно, а высказывание «Если в Екатеринбурге проживает более одного миллиона человек, то Екатеринбург – столица России» (p
q) истинно, а высказывание «Если в Екатеринбурге проживает более одного миллиона человек, то Екатеринбург – столица России» (p 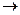 q) ложно.
q) ложно.
У каждого, кто впервые знакомится с истинностными таблицами для пропозициональных связок, естественно возникает вопрос, почему в своих строках они имеют те, а не иные значения. Почему, например, импликация в четвёртой строке своей истинностной таблицы истинна, а не ложна? Или, более общо, откуда вообще берутся те определения пропозициональных связок, которые находят своё отражение в истинностных таблицах? Конечно, эти определения не берутся логиками из головы, а рассматриваются ими как отражения языковой практики людей, т. е. практики использования людьми выражений «не», «и», «или», «если, то» и др. Определения пропозициональных связок являются моделями, с помощью которых описываются свойства этих выражений, выступающих в качестве оригиналов. Однако соответствие между моделью и оригиналом всегда бывает частичным, а не полным. То, что определения пропозициональных связок в общем и целом соответствуют языковой практике людей, ни у кого не вызывает сомнений. Более того, эти определения, ставшие с конца 19 в. неотъемлемой частью логики высказываний, уходят своими корнями во времена античности, когда их впервые стали использовать представители мегарской школы.
Используя истинностные таблицы для пропозициональных связок, мы можем построить истинностную таблицу для любого высказывания, записанного на языке логики высказываний. Такая таблица показывает, при каких условиях наше высказывание истинно, а при каких – ложно, т. е. даёт обзор условий его истинности. Для того чтобы проиллюстрировать процедуру построения истинностной таблицы, возьмём в качестве примера высказывание «Если я устал или голоден, то я не могу готовиться к занятиям». Обозначив его просты компоненты буквами p, q и r, мы получим формулу
(p 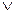 q)
q) 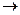 ~ r,
~ r,
построенную из них с помощью трёх пропозициональных связок – дизъюнкции, импликации и отрицания. Структура полученной нами формулы указывает на то, что при её построении вначале использовались дизъюнкция (p 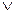 q) и отрицание (~ r), а затем они были соединены с помощью импликации ((p
q) и отрицание (~ r), а затем они были соединены с помощью импликации ((p 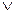 q)
q) 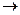 ~ r). Поскольку эта формула построена из трёх пропозициональных переменных p, q и r, каждая из которых может быть либо истинной, либо ложной, число строк в её истинностной таблице равно восьми. Вообще число строк в истинностной таблице определяется по формуле 2n, где 2 – постоянная величина, равная числу истинностных значений, а n – число пропозициональных переменных, которое больше или равно единице, но всегда конечно. Итак, построив две вспомогательные таблицы для формул p
~ r). Поскольку эта формула построена из трёх пропозициональных переменных p, q и r, каждая из которых может быть либо истинной, либо ложной, число строк в её истинностной таблице равно восьми. Вообще число строк в истинностной таблице определяется по формуле 2n, где 2 – постоянная величина, равная числу истинностных значений, а n – число пропозициональных переменных, которое больше или равно единице, но всегда конечно. Итак, построив две вспомогательные таблицы для формул p 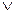 q и ~ r, мы получаем в конечном счёте истинностную таблицу формулы (p
q и ~ r, мы получаем в конечном счёте истинностную таблицу формулы (p 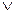 q)
q) 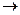 ~ r :
~ r :
| p | q | r | p 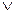 q q
| ~ r | (p 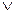 q) q) 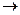 ~ r ~ r
|
Как видно из этой таблицы, высказывание «Если я устал или голоден, то я не могу готовиться к занятиям» истинно в пяти из восьми возможных случаев, а ложно – в трёх.
Дата добавления: 2020-12-11; просмотров: 614;











