Мінімізація логічних функцій

Метою мінімізації є зменшення вартості технічної реалізації логічних функцій незалежно від використовуваних апаратних засобів.

Логічні функції апаратно реалізуються за допомогою мікросхем, орієнтованих на виконання тих чи інших операцій. Мікросхеми загального використання здебільшого можуть реалізовувати декілька простих одиночних операцій. З цієї причини справедливо стверджувати, що чим простішою є аналітична форма запису логічної функції, тим менше використовується логічних елементів і, як результат, тим менше мікросхем необхідно для її реалізації. Складність логічних функцій визначається кількістю логічних змінних, що входять до їх складу в прямому і інверсному виді, та кількістю простих логічних операцій над ними. Будь-яка логічна функція може бути записана різними аналітичними виразами різного рівня складності. Серед них можна знайти такі, які містять мінімальну кількість логічних змінних і операцій над ними. Задача знаходження таких аналітичних виразів називається мінімізацією логічних функцій. Звідси витікає, що мінімізація логічної функції – це заміна логічної функції, що представлена у вигляді логічної суми мінтермів або логічного добутку макстермів, іншою логічною функцією з мінімальною кількістю логічних змінних та операцій над ними.

Задача мінімізації – це задача неоднозначна, і різними шляхами можна отримати різні вирази мінімізованої функції, які відрізнятимуться між собою кількістю змінних і операцій над ними.

Аналітичний спосіб мінімізації. Для зменшення складності логічних функцій здебільшого використовуються операції склеювання:

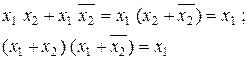
та поглинання:

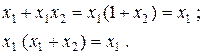
Як приклад, розглянемо процедуру спрощення наступної функції:

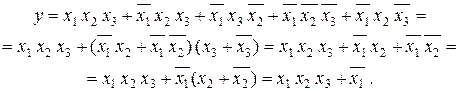
Одержана ДНФ має мінімальну складність.

Мінімізація за допомогою карт Карно (діаграм Вейча).Метод, оснований на використанні карт Карно, характеризується своєю простотою і наочністю. Зображення функції в площині координат її параметрів, подібно до алгебраїчних функцій, дозволяє наглядно встановити взаємозв’язки між її змінними і, як результат, виділити ті змінні, які є домінуючими в її визначенні.

Для пояснення методу перш за все сформулюємо основні властивості карт Карно:

· клітини карти, координати яких відрізняються лише параметрами однієї змінної, називаються сусідніми;

· сусідні клітини, значення функцій в яких або тільки істинні, або тільки хибні, можуть об’єднуватися в групи по 2^m клітин, де m – ціле число (m = 0, 1, 2, 3, …);

· при переході до аналітичної форми запису логічної функції з карти Карно вона може записуватись незмінними координатами об’єднаних груп клітин;

· у випадку неповністю визначеної функції невизначені клітини можуть бути довизначеними, виходячи з умови одержання більшої кількості об’єднаних клітин;

· одна клітина може об’єднуватись у декілька груп.

Використання карт Карно для мінімізації логічних функцій базується на наглядному використанні операції склеювання. Дійсно, дві сусідні клітки відрізняються лише однією змінною. Тому, об’єднуючи їх, ми записуємо лише незмінні координати, тобто виносимо їх за дужки. У дужках залишаються змінні координати, які об’єднуються в одну операцією склеювання. Для отримання мінімального значення функції, представленого картою Карно, окрім правил, викладених вище, необхідно користуватись загальним правилом: одиниці або нулі повинні об’єднуватись мінімальним числом найбільших контурів.

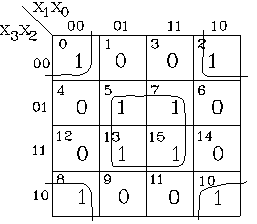
Рис.2.2.

Приклад 2.8. Мінімізувати логічну функцію, що представлена у вигляді карти Карно (рис. 2.2).

Розв’язання. Об’єднуючи сусідні клітини з істинними значеннями функції (тобто клітини 0, 2, 8, 10 та клітини 5, 7, 13, 15), записуємо їх незмінні координати:

· для центральних клітин: ;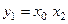

· для крайніх клітин: .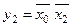

Мінімізована логічна функція має вигляд:

.

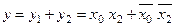Аналогічний результат буде одержаний і при об’єднанні клітин з нулями. Для вертикальної групи клітин (клітини 1, 3, 9, 11) знаходимо:

.

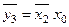Для групи горизонтальних клітин (клітини 4, 6, 12, 14):

.

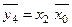Мінімізована функція

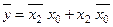
операцією інверсії та теоремою де Моргана зводиться до отриманої раніше.

За допомогою карт Карно легко вирішуються задачі мінімізації функцій з кількістю змінних до шести включно. При більшій кількості змінних пошук мінімальних форм запису функцій значно ускладнюється і наочність карт Карно втрачається.

Мінімізація неповністю визначених логічних функцій. Серед логічних функцій зустрічаються такі, досконалі форми яких містять невизначені мінтерми (макстерми). З точки зору інженерної практики це означає, що електронна апаратура, яка розробляється, повинна бути байдужою до відповідних комбінацій логічних змінних. Зустрічаються й інші ситуації, при яких в деяких комбінаціях змінних має місце неоднозначність логічної функції. В обох випадках наявність неоднозначності використовується з метою забезпечення мінімальної форми логічної функції.

Розглянемо приклад логічної функції, що приведена на рис. 2.3.

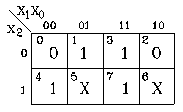
Рис.2.3.

Невизначеність її значень, що відображена у клітинах 5 та 6, може бути використана для мінімізації. Підстановка в указані клітини значень “1” дає можливість об’єднати групи клітин 1, 3, 5, 7 і 4, 5, 6, 7 та одержати мінімізовану функцію:

.

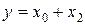Слід зазначити, що для більш складних функцій можуть використовуватись декілька різних способів довизначення, в результаті можна отримувати мінімальні функції різної складності.

Недовизначені функції часто зустрічаються при реалізації перетворювачів кодів.