СИММЕТРИЧНЫХ СОСТАВЛЯЮЩИХ

Метод симметричных составляющих основан на представлении произвольной несимметричной трехфазной системы ЭДС, напряжений или токов в виде суммы трех симметричных систем — составляющих прямой, обратной и нулевой последовательностей.

Рассмотрим несимметричную трехфазную систему токов, векторное

изображение которой приведено на рис. 10.7, а. Представим каждый из токов в виде суммы трех величин:

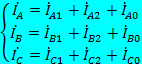
в которой первая группа слагаемых İA1, İB1, İC1 образует симметричную систему прямой последовательности, имеет одинаковые модули и фазовые сдвиги на 120° и прямой порядок следования фаз AВС (рис. 10.7,6), такой же, как принятый при анализе симметричных систем. Вторая группа слагаемых İA2, İB2, İC2 образует симметричную систему обратной последовательности с порядком следования фаз АСВ (рис. 10.7, в).

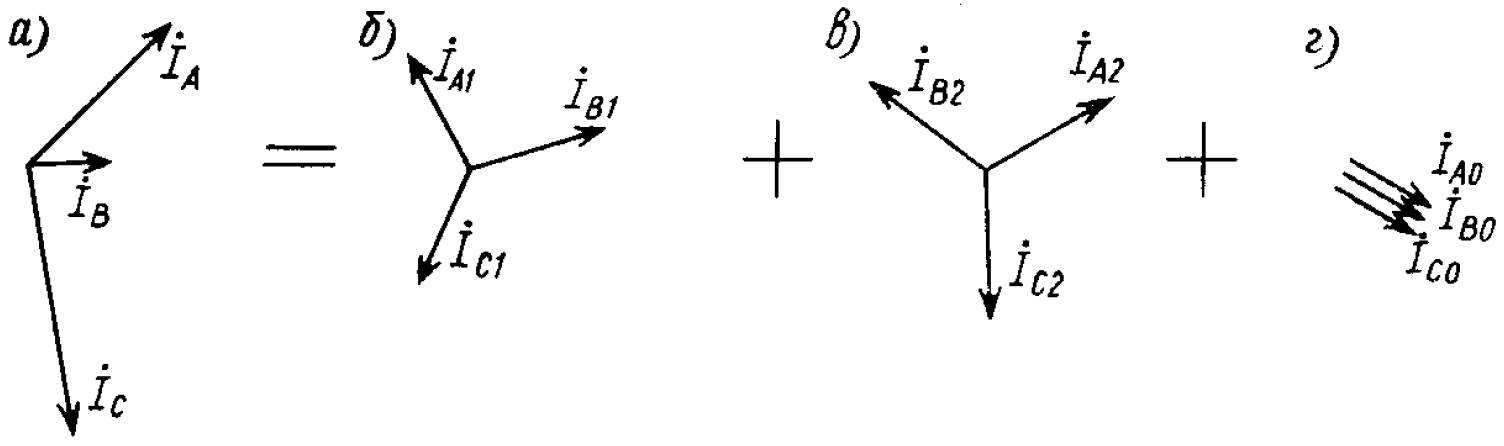
Рис. 10.7

Наконец, система составляющих нулевой последовательности İA0, İB0, İC0 включает три одинаковых вектора, совпадающих по фазе (рис. 10.7, г).

При записи выражений отдельных составляющих используем сокращенную запись с помощью

оператора а — комплексного множителя .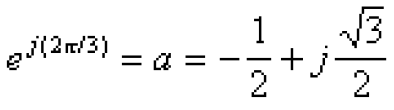

В дальнейших преобразованиях будут использованы соотношения:

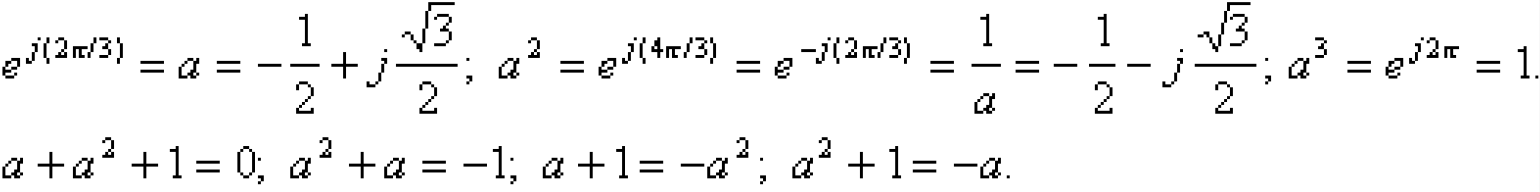
Применение оператора а позволяет записать для составляющих:

прямой последовательности

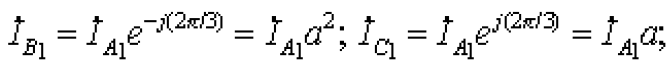
обратной последовательности

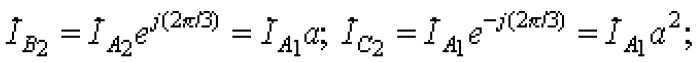
нулевой последовательности

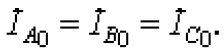
Подстановкой этих связей в исходную систему для результирующих токов

приводим ее к виду:

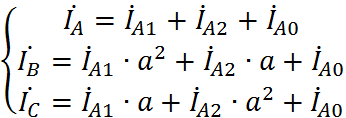
из которого симметричные составляющие фазы A (İA1, İA2 и İA0) можно легко выразить через суммарные токи исходной несимметричной системы:

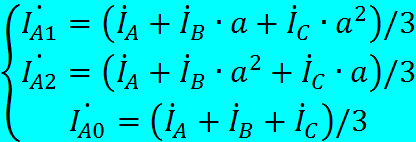
Эти выражения показывают, что разложение произвольной несимметричной системы токов İA, İB, İC на симметричные составляющие существует всегда и является единственным.

Аналогичные соотношения имеют место для симметричных составляющих трехфазных систем напряжений и ЭДС. Разложение несимметричных систем позволяет свести задачу расчета несимметричной трехфазной пени к анализу совокупности трех симметричных режимов для составляющих прямой, обратной и нулевой последовательностей.