Каждая из этих составляющих вызывает прямой изгиб бруса в одной из главных плоскостей.

Сила F_x – в плоскости zOx и сила F_у в плоскости zOy.

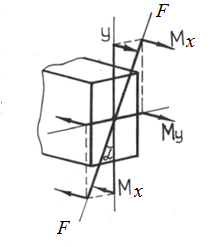Следовательно косой изгиб можно рассматривать как совокупность двух прямых изгибов во взаимноперпендикулярных плоскостях, проходящих через главные центральные оси.

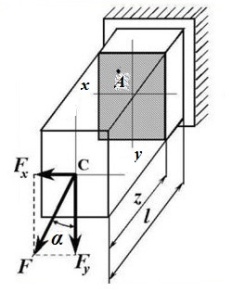
Применим метод сечений и рассмотрим равновесие отсеченной части бруса длиной ℓ.

В произвольном сечении бруса возникают два изгибающих момента: M_y относительно главной оси Ох и M_x относительно главной оси Оy

(поперечные силы не будем принимать во внимание).

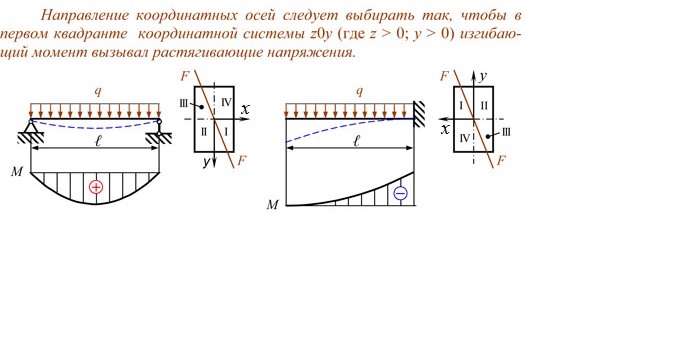
Направление координатных осей следует выбирать так, чтобы в первом квадранте координатной системы хОу (где х > 0, у > 0) изгибающий момент вызывал растягивающие напряжения.

Сравним выбор системы координат на следующих рисунках.

Правило знаков для внутренних усилий:

изгибающие моменты – положительные, если вызывают растяжение в положительном квадранте координатной системы хOy;

поперечные силы – положительны, если под их действием отсеченный элемент поворачивается по часовой стрелке.

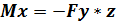
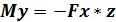
При условии, что z = ℓ

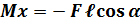
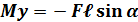
Для определения полного изгибающего момента M и полной поперечной силы Q при косом изгибе достаточно определить внутренние усилия для каждого из плоских изгибов в отдельности (то есть Qy, Mz и Qz, My), а затем найти их векторную сумму:

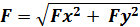
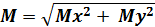
Дата добавления: 2017-06-13; просмотров: 1122;