Глава 4. Матрицы и дифференциальные уравнения
Теория матриц является эффективным средством исследования и решения дифференциальных уравнений. Среди них наиболее простыми являются линейные дифференциальные уравнения с постоянными коэффициентами, к которым приводятся многие задачи физики и техники. Здесь рассматриваются только такие уравнения, и для краткости будем называть их просто дифференциальными уравнениями. Дифференциальное уравнение первого порядка, относительно неизвестной функции 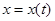 имеет вид
имеет вид
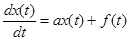 ,
,
где  – постоянный коэффициент;
– постоянный коэффициент; 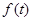 – непрерывная функция времени, определенная на некотором интервале
– непрерывная функция времени, определенная на некотором интервале 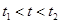 . Решением уравнения является функция
. Решением уравнения является функция 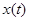 , подстановка которой в это уравнение обращает его в тождество. При
, подстановка которой в это уравнение обращает его в тождество. При 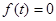 уравнение называется однородным и его общее решение выражается как
уравнение называется однородным и его общее решение выражается как 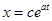 , где
, где 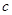 – произвольная постоянная. Общее решение исходного неоднородного уравнения (
– произвольная постоянная. Общее решение исходного неоднородного уравнения ( 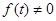 ) выражается формулой
) выражается формулой
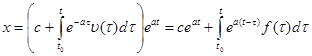 .
.
Это решение представляет собой сумму общего решения однородного и частного решения неоднородного дифференциальных уравнений. Оно удовлетворяет начальному условию 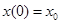 при
при 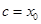 , т. е.
, т. е.
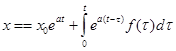 .
.
Переходя к системам дифференциальных уравнений, рассмотрим их представление в нормальной форме:
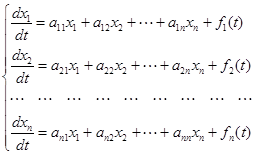 ,
,
к которой, как известно, можно привести любую систему линейных дифференциальных уравнений. В матричной записи эта система представляется одним уравнением
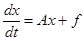 ,
,
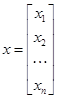
где 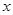 – вектор (столбец) неизвестных функций
– вектор (столбец) неизвестных функций 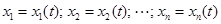 ;
; 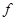 – вектор (столбец) задающих функций
– вектор (столбец) задающих функций 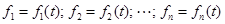 и
и 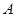 – квадратная матрица постоянных коэффициентов
– квадратная матрица постоянных коэффициентов 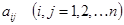 :
:
 ;
; 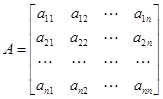 ;
; 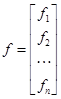 .
.
Задачу об отыскании решения системы дифференциальных уравнений, удовлетворяющих заданным начальным значениям скаляра 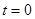 и вектора
и вектора 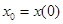 , называют задачей Коши. По аналогии с дифференциальным уравнением первого порядка можно записать искомое решение для вектора неизвестных функций в виде:
, называют задачей Коши. По аналогии с дифференциальным уравнением первого порядка можно записать искомое решение для вектора неизвестных функций в виде: 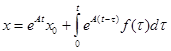 .
.
Необходимо установить допустимость такого представления решения, а также выяснить смысл и способы определения входящей в него матрицы 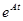 .
.
В матричной форме нормальная однородная система дифференциальных уравнений ( 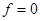 ) имеет вид:
) имеет вид: 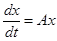 . Будем искать ее решение в виде
. Будем искать ее решение в виде 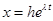 где
где 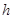 вектор (столбец) произвольных постоянных. Подставляя
вектор (столбец) произвольных постоянных. Подставляя 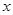 в исходное уравнение, получаем
в исходное уравнение, получаем 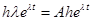 или после сокращения на скаляр
или после сокращения на скаляр 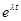 и перенесения
и перенесения 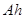 в левую часть равенства:
в левую часть равенства: 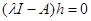 . Заметим, что сокращать на вектор
. Заметим, что сокращать на вектор 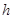 нельзя, так как операция деления на вектор в общем случае не имеет смысла. Вынося за скобки вектор
нельзя, так как операция деления на вектор в общем случае не имеет смысла. Вынося за скобки вектор 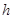 , необходимо умножить предварительно
, необходимо умножить предварительно 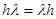 на единичную матрицу
на единичную матрицу 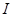 . Уравнение
. Уравнение 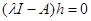 имеет нетривиальные решения при условии, что определитель матрицы
имеет нетривиальные решения при условии, что определитель матрицы 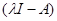 обращается в нуль, т. е.
обращается в нуль, т. е. 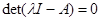 или
или
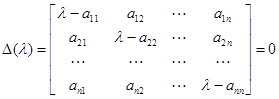 .
.
Так как порядок матрицы 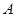 равен
равен 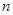 , то
, то  является многочленом
является многочленом 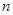 -й степени относительно
-й степени относительно 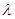 , т. е.
, т. е.  . Корни уравнения
. Корни уравнения 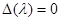 (нули многочлена
(нули многочлена  ), число которых равно
), число которых равно 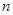 , дадут значения
, дадут значения 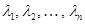 при которых исходная система имеет нетривиальные решения. Рассмотрим наиболее простой случай, когда все корни уравнения
при которых исходная система имеет нетривиальные решения. Рассмотрим наиболее простой случай, когда все корни уравнения 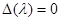 простые (попарно различные). Тогда при
простые (попарно различные). Тогда при 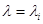 имеем однородное уравнение
имеем однородное уравнение 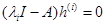 , из которого можно определить вектор
, из которого можно определить вектор 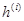 .Таким образом, решение нормальной системы дифференциальных уравнений, соответствующее корню
.Таким образом, решение нормальной системы дифференциальных уравнений, соответствующее корню 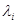 , будет
, будет 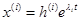 . Всего получим
. Всего получим 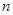 таких решений, соответствующих
таких решений, соответствующих 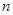 корням
корням 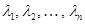 .
.
Для любой квадратной матрицы 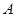 по установившейся терминологии
по установившейся терминологии 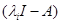 называется характеристической матрицей, а
называется характеристической матрицей, а 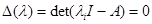 – характеристическим уравнением. Корни
– характеристическим уравнением. Корни 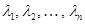 уравнения
уравнения 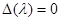 называются собственными значениями (характеристическими числами), а векторы
называются собственными значениями (характеристическими числами), а векторы 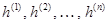 собственными векторами матрицы
собственными векторами матрицы 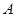 . Совокупность собственных значений
. Совокупность собственных значений 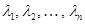 называется спектром матрицы
называется спектром матрицы 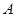 .
.
Множество всех решений однородной системы дифференциальных уравнений образует 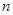 -мерное линейное пространство с базисом
-мерное линейное пространство с базисом 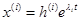
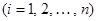 . Общее решение имеет следующий вид:
. Общее решение имеет следующий вид:
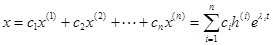 .
.
Это выражение может быть представлено в матричной форме
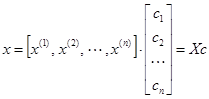 .
.
В свою очередь матрица 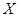 выражается следующим образом
выражается следующим образом
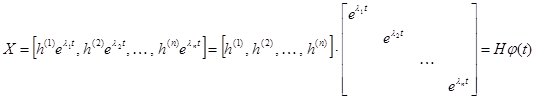 .
.
Здесь через 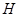 обозначена матрица
обозначена матрица 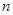 -го порядка, называемая модальной и состоящая из столбцов
-го порядка, называемая модальной и состоящая из столбцов 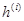 , а элементами диагональной матрицы
, а элементами диагональной матрицы 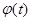 являются экспоненциальные функции
являются экспоненциальные функции 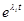 .
.
Итак, решение нормальной однородной системы линейных дифференциальных уравнений представляется в виде 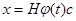 .
.
При 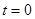 матрица
матрица 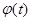 равна единичной матрице, следовательно, начальное условие
равна единичной матрице, следовательно, начальное условие  , откуда
, откуда 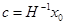 . Подставляя это значение
. Подставляя это значение 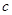 в общее решение, получаем
в общее решение, получаем 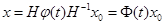 . Матрица
. Матрица 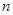 -го порядка
-го порядка 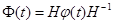 называется фундаментальной матрицей. Ее вычисление сводится к определению собственных значений и собственных векторов матрицы
называется фундаментальной матрицей. Ее вычисление сводится к определению собственных значений и собственных векторов матрицы 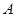 системы дифференциальных уравнений.
системы дифференциальных уравнений.
Рассмотрим в качестве примера однородную систему дифференциальных уравнений:
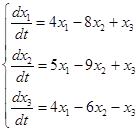 .
.
Для этой системы
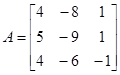 ;
; 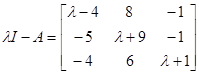 .
.
Поскольку для вычисления 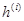 необходимы алгебраические дополнения какой-либо строки матрицы
необходимы алгебраические дополнения какой-либо строки матрицы 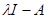 , то определитель этой матрицы удобно получать разложением по элементам той же строки.
, то определитель этой матрицы удобно получать разложением по элементам той же строки.
Алгебраические дополнения элементов первой строки:
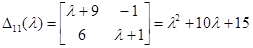 ;
;
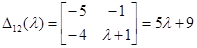 ;
;
 .
.
Характеристический многочлен и собственные значения:
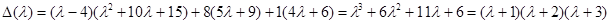 ;
;
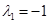 ;
; 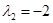 ;
; 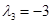 .
.
Собственные векторы 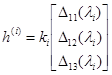 :
: 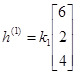 ;
; 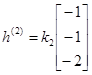 ;
; 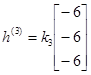 .
.
Принимая 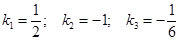 (эти значения произвольны и выбираются по соображениям удобства), получаем модальную матрицу, а также обратную к ней:
(эти значения произвольны и выбираются по соображениям удобства), получаем модальную матрицу, а также обратную к ней:
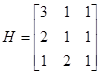 ;
; 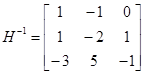
Фундаментальная матрица
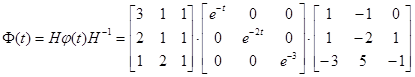 ,
,
что после перемножения матриц приводит к следующему результату
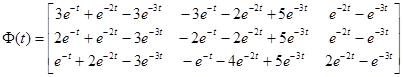 .
.
Таким образом, в соответствии с соотношением 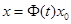 общее решение рассматриваемой однородной системы дифференциальных уравнений:
общее решение рассматриваемой однородной системы дифференциальных уравнений:
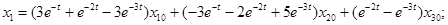
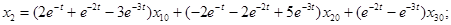
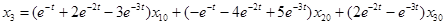 ,
,
где 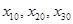 элементы вектора
элементы вектора 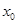 , равные начальным значениям соответствующих переменных при
, равные начальным значениям соответствующих переменных при 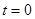 .
.
Выясним характер фундаментальной матрицы 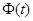 . Подставляя решение
. Подставляя решение 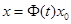 в однородное дифференциальное уравнение
в однородное дифференциальное уравнение 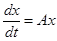 , получаем тождества:
, получаем тождества:
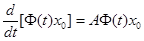 ;
; 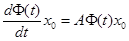 .
.
Так как в этих тождествах 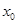 – вектор начальных значений не зависящий от времени, то
– вектор начальных значений не зависящий от времени, то 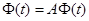 , т. е.
, т. е. 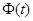 – это такая матрица, производная которой по времени равна произведению матрицы
– это такая матрица, производная которой по времени равна произведению матрицы 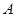 на саму матрицу. Аналогичными свойствами обладает единственная скалярная функция
на саму матрицу. Аналогичными свойствами обладает единственная скалярная функция  , поэтому по аналогии можно записать следующие соотношения:
, поэтому по аналогии можно записать следующие соотношения:
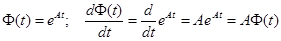 .
.
Через экспоненциальную функцию выражаются также другие функции от матриц:
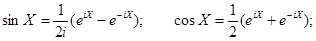


Следует иметь в виду, что 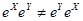 , а соотношение
, а соотношение 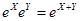 имеет смысл только в случаях, когда
имеет смысл только в случаях, когда 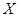 и
и 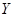 – перестановочные матрицы.
– перестановочные матрицы.
Решение неоднородной 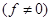 системы дифференциальных уравнений может быть записано в матричной форме
системы дифференциальных уравнений может быть записано в матричной форме 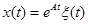 , где
, где 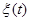 – векторная функция времени, подлежащая определению. Подставляя выражение для
– векторная функция времени, подлежащая определению. Подставляя выражение для 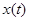 и ее производной в исходное уравнение, имеем:
и ее производной в исходное уравнение, имеем:
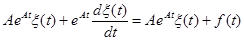
или после очевидных упрощений
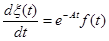 .
.
При начальных условиях 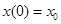 начальное значение искомой функции
начальное значение искомой функции 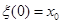 . Интегрированием получаем
. Интегрированием получаем
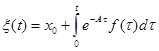 .
.
Используя это выражение, находим решение неоднородного уравнения, удовлетворяющее начальному условию 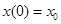 :
:
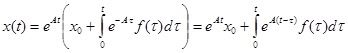 ,
,
которое называется формулой Коши. Его можно рассматривать как сумму решения соответствующего однородного уравнения (при 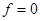 ) и решения неоднородного уравнения при нулевых начальных условиях (
) и решения неоднородного уравнения при нулевых начальных условиях ( 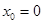 ).
).
Пусть дана неоднородная система дифференциальных уравнений в нормальной форме:
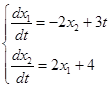 .
.
Для этой системы:
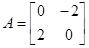 ;
; 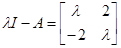 ;
; 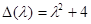 ;
;
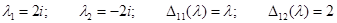 ;
;
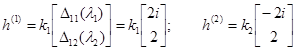 .
.
Полагая для удобства 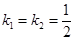 , находим модальную матрицу
, находим модальную матрицу 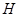 и обратную к ней матрицу
и обратную к ней матрицу 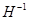 :
:
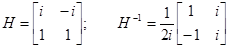 ,
,
после чего определяется фундаментальная матрица:
 .
.
Решение задачи Коши для однородной системы:
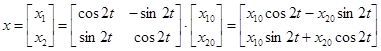 .
.
Найдем интеграл в выражении для частного решения неоднородной системы при 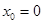 :
:
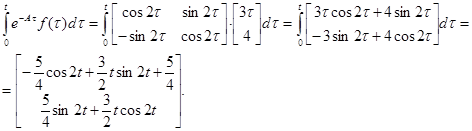
Частное решение неоднородной системы:
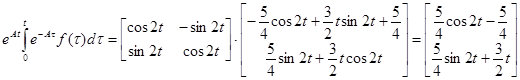 .
.
Таким образом, решение неоднородной системы, удовлетворяющей начальным условиям 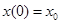 , запишется следующим образом:
, запишется следующим образом:
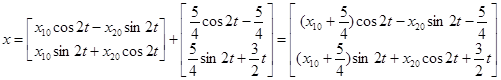 .
.
Контрольные вопросы к лекции 12
12-1. Как записывается система уравнений в матричном виде?
12-2. Как решается матричное уравнение 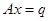 ?
?
12-3. Что представляет собой определитель матрицы?
12-4. Как вычисляется определитель второго порядка?
12-5. Как вычисляется определитель третьего порядка?
12-6. В чем состоит свойство антисимметрии определителя?
12-7. В каком случае определитель равен нулю?
12-8. Как изменяется определитель матрицы 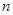 -го порядка при умножении ее на скаляр?
-го порядка при умножении ее на скаляр?
12-9. Как вычисляется алгебраическое дополнение?
12-10. Как вычисляется обратная матрица?
12-11. Опишите алгоритм вычисления обратной матрицы методом исключения.
12-12. Какие матрицы называются особенными?
12-13. Для каких матриц существуют обратные матрицы?
12-14. Какая матрица называется инволютивной?
12-15. Что называется рангом матрицы?
12-16. Что называется дефектом матрицы?
12-17. Какая система уравнений называется совместной?
12-18. В чем состоит суть теоремы Кронекера – Капелли?
12-19. Какая система уравнений называется неопределенной?
12-20. Опишите алгоритм Гаусса для решения неоднородных систем линейных уравнений 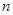 -го порядка?
-го порядка?
12-21. Опишите алгоритм Гаусса – Жордана для решения неоднородных систем линейных уравнений 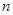 -го порядка?
-го порядка?
12-22. Какая система уравнений называется однородной?
12-23. Как определяется характеристическая матрица для квадратной матрицы 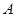 ?
?
12-24. Как определяется характеристическое уравнение?
12-25. Что называется характеристическими числами квадратной матрицы 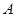 ?
?
12-26. Что называется спектром квадратной матрицы 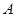 ?
?
12-27. Какая матрица называется модальной?
12-28. Какая матрица называется фундаментальной?
12-29. Что представляет собой решение неоднородного дифференциального уравнения в форме Коши?
Дата добавления: 2016-09-06; просмотров: 10382;











