Глава 4. Алгебра предикатов
Обычно высказывания выражают свойства одного или нескольких объектов. Содержательная часть высказывания играет роль определяющего свойства совокупности объектов, для которых это высказывание истинно, и называется предикатом.
В то время как логика высказываний проявляет интерес только к логической связи между предложениями, логика предикатов проникает и в структуру самих предложений в смысле связи того, о ком или о чем идет речь (субъект) с тем, что говорится о данном предмете (предикат). Поэтому язык логики предикатов лучше приспособлен для выражения логических связей между различными понятиями и утверждениями.
Например, высказывание «Иванов – отличник» истинно или ложно в зависимости от оценок, которые имеет данный студент. В то же время предикат «  – отличник» определяет подмножество отличников на некотором множестве студентов (группа, курс, факультет). Подставив вместо
– отличник» определяет подмножество отличников на некотором множестве студентов (группа, курс, факультет). Подставив вместо  фамилии студентов, получим множество высказываний. Совокупность истинных высказываний и будет соответствовать подмножеству отличников.
фамилии студентов, получим множество высказываний. Совокупность истинных высказываний и будет соответствовать подмножеству отличников.
Предикат представляет собой логическую функцию 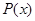 , принимающую, как и булевы функции, значение 0 или 1, но в отличие от них, значения аргумента
, принимающую, как и булевы функции, значение 0 или 1, но в отличие от них, значения аргумента  выбираются из некоторого множества
выбираются из некоторого множества 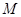 объектов (
объектов ( 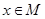 ). В общем случае такая функция может зависеть от многих аргументов
). В общем случае такая функция может зависеть от многих аргументов 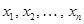 , принимающих значения из одного и того же или различных множеств. Ее записывают
, принимающих значения из одного и того же или различных множеств. Ее записывают 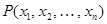 и называют
и называют 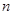 -местным предикатом.
-местным предикатом.
Аргументы 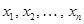 называются предметными переменными. Конкретные значения аргументов называют предметными постоянными. Предметные переменные и предметные постоянные образуют класс логических понятий, называемых термами.
называются предметными переменными. Конкретные значения аргументов называют предметными постоянными. Предметные переменные и предметные постоянные образуют класс логических понятий, называемых термами.
Например: «  – четное число», «
– четное число», «  – компонент цепи» являются одноместными предикатами
– компонент цепи» являются одноместными предикатами 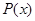 ; «
; «  брат
брат 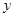 », «
», «  меньше
меньше 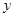 » – двуместные предикаты
» – двуместные предикаты 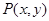 ; «
; «  и
и 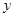 – родители
– родители 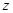 », «
», «  – сумма
– сумма 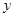 и
и 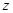 » – трехместные предикаты
» – трехместные предикаты 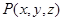 и т. д. Если все аргументы
и т. д. Если все аргументы 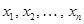 замещены конкретными значениями (объектами), то предикат переходит в высказывание, которое рассматривают как
замещены конкретными значениями (объектами), то предикат переходит в высказывание, которое рассматривают как 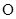 -местный предикат.
-местный предикат.
Так как предикаты способны принимать только значения 0 и 1, то их, как и булевы переменные, можно связывать логическими операциями. В результате получаем формулы, определяющие более сложные предикаты. Так, если 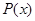 означает «
означает «  – инженер», а
– инженер», а 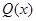 – «
– «  – сотрудник нашего отдела», то
– сотрудник нашего отдела», то 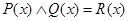 есть одноместный предикат «
есть одноместный предикат «  – инженер и сотрудник нашего отдела» или проще «
– инженер и сотрудник нашего отдела» или проще «  – инженер нашего отдела». Очевидно, если
– инженер нашего отдела». Очевидно, если  – множество инженеров, а
– множество инженеров, а 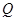 – множество сотрудников данного отдела, то этот предикат соответствует пересечению
– множество сотрудников данного отдела, то этот предикат соответствует пересечению 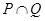 . Таким образом, имеет место тесная связь между логикой предикатов и операциями над множествами.
. Таким образом, имеет место тесная связь между логикой предикатов и операциями над множествами.
В логике предикатов большое значение имеют две операции, называемые кванторами, с помощью которых выражают отношения общности и существования. Пусть 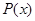 – предикат, определенный на множестве
– предикат, определенный на множестве 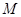 . Утверждение, что все
. Утверждение, что все 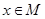 обладают свойством
обладают свойством 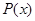 , записывают с помощью квантора общности
, записывают с помощью квантора общности 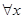 в виде
в виде 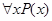 , что читается «для всех
, что читается «для всех  ,
,  от
от  ». Утверждение, что существует хотя бы один объект
». Утверждение, что существует хотя бы один объект  из
из 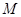 , обладающий свойством
, обладающий свойством 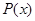 , записывают с помощью квантора существования
, записывают с помощью квантора существования 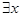 в виде
в виде 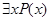 , что читается «существует такое
, что читается «существует такое  , что
, что  от
от  ».
».
Хотя в выражениях 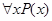 и
и 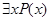 и встречается буква
и встречается буква  , но они не зависят от значений этой переменной. Кванторы
, но они не зависят от значений этой переменной. Кванторы 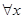 и
и 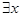 связывают переменную
связывают переменную  , превращая одноместный предикат в высказывание. Очевидно,
, превращая одноместный предикат в высказывание. Очевидно, 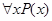 истинно только при условии, что
истинно только при условии, что 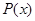 тождественно истинный предикат, а во всех остальных случаях это высказывание ложно, высказывание
тождественно истинный предикат, а во всех остальных случаях это высказывание ложно, высказывание 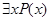 всегда истинно, кроме единственного случая, когда
всегда истинно, кроме единственного случая, когда 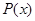 – тождественно ложный предикат.
– тождественно ложный предикат.
Рассмотрим, например, предикат 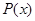 «
«  – простое число», определенный на множестве натуральных чисел. Подставляя вместо
– простое число», определенный на множестве натуральных чисел. Подставляя вместо  числа натурального ряда, получаем счетное множество высказываний. Некоторые из них, например
числа натурального ряда, получаем счетное множество высказываний. Некоторые из них, например 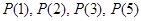 и т. д., являются истинными. Высказывание
и т. д., являются истинными. Высказывание 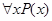 – «все натуральные числа простые» – ложно, а
– «все натуральные числа простые» – ложно, а 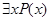 – «некоторые из натуральных чисел – простые» – истинно. Между кванторами
– «некоторые из натуральных чисел – простые» – истинно. Между кванторами 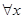 и
и 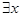 имеют место соотношения, обобщающие законы де Моргана:
имеют место соотношения, обобщающие законы де Моргана: 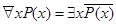 ;
; 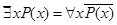 .
.
Применение квантора к 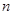 -местному предикату превращает его в
-местному предикату превращает его в 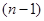 -местный предикат. Кванторы можно также применять к нескольким различным переменным (по одному квантору какого-либо типа к каждой переменной). Если к
-местный предикат. Кванторы можно также применять к нескольким различным переменным (по одному квантору какого-либо типа к каждой переменной). Если к 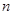 -местному предикату применяется
-местному предикату применяется 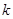 кванторов, то он превращается в
кванторов, то он превращается в 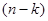 -местный предикат, а при
-местный предикат, а при 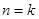 – в высказывание. Переменные, к которым применяются кванторы, называются связанными, а остальные переменные – свободными. Например, из двухместного предиката
– в высказывание. Переменные, к которым применяются кванторы, называются связанными, а остальные переменные – свободными. Например, из двухместного предиката 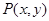 с помощью кванторов получаем одноместные предикаты
с помощью кванторов получаем одноместные предикаты 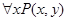 ;
; 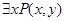 ;
; 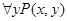 и
и 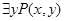 , а также высказывания
, а также высказывания 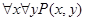 ;
; 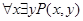 ;
; 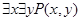 и т. п.
и т. п.
Порядок следования одноименных кванторов не имеет значения, но разноименные кванторы переставлять нельзя. Так, 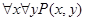 эквивалентно
эквивалентно 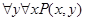 , но высказывания
, но высказывания 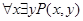 и
и 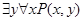 , вообще говоря, различны. В этом можно убедиться на примере предиката
, вообще говоря, различны. В этом можно убедиться на примере предиката 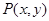 =«
=«  делит
делит 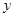 », который в первом случае превращается в высказывание «для всякого
», который в первом случае превращается в высказывание «для всякого  существует такое
существует такое 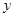 , что
, что  делит
делит 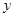 » (истинно), а во втором – «существует такое
» (истинно), а во втором – «существует такое 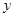 , что любое
, что любое  делит
делит 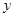 » (ложно).
» (ложно).
Квантор связывает переменную в области своего действия. Эта область обычно заключается в скобки, если она содержит не один предикат, а совокупность предикатов, связанных символами логических операций. Выражения, которые можно образовать применением к предикатам сентенциональных связок и кванторов, представляют собой формулы логики предикатов. Переменная свободна в формуле, если хотя бы на одно ее вхождение не распространяется действие квантора. Переменная связана в формуле, если она связана по меньшей мере одним квантором. Например, в формуле 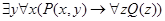 вхождение каждой из переменных связано, а в формуле
вхождение каждой из переменных связано, а в формуле 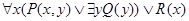 переменная
переменная  одновременно и свободная и связанная.
одновременно и свободная и связанная.
Перевод предложений с русского или какого-либо другого языка на символический язык логики предикатов вызывает определенные трудности из-за отсутствия механических правил. Он основан не столько на форме обычных предложений, сколько на выявлении их смысловой связи.
В традиционной логике большое внимание уделяется четырем типам категорических высказываний, которые обычно обозначаются заглавными латинскими буквами 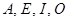 :
:
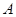 – общеутвердительное высказывание «всякое
– общеутвердительное высказывание «всякое 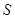 суть
суть  »:
»: 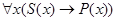 , что означает: «Для всех
, что означает: «Для всех  , если
, если  обладает свойством
обладает свойством 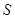 , то
, то  обладает и свойством
обладает и свойством  »;
»;
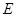 – общеотрицательное высказывание «никакое
– общеотрицательное высказывание «никакое 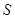 не есть
не есть  »:
»: 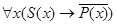 , что означает «для всех
, что означает «для всех  , если
, если  обладает свойством
обладает свойством 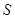 , то он не обладает свойством
, то он не обладает свойством  »;
»;
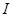 – частноутвердительное высказывание «некоторые
– частноутвердительное высказывание «некоторые 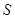 суть
суть  »:
»: 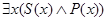 , что означает «существует такой объект
, что означает «существует такой объект  , обладающий свойством
, обладающий свойством 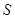 , который также обладает свойством
, который также обладает свойством  »;
»;
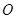 – частноотрицательное высказывание «некоторые
– частноотрицательное высказывание «некоторые 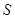 не суть
не суть  »:
»: 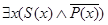 , что означает «существует такой объект
, что означает «существует такой объект  , который обладает свойством
, который обладает свойством 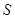 и не обладает свойством
и не обладает свойством  ».
».
Пусть, например, 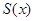 = «
= «  – селедка» (свойство «быть селедкой») и
– селедка» (свойство «быть селедкой») и 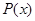 – «
– «  – рыба» (свойство «быть рыбой»). Тогда четырем типам категорических высказываний соответствуют следующие утверждения:
– рыба» (свойство «быть рыбой»). Тогда четырем типам категорических высказываний соответствуют следующие утверждения: 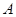 = «Всякая селедка – рыба»;
= «Всякая селедка – рыба»; 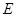 – «Никакая селедка не является рыбой»;
– «Никакая селедка не является рыбой»; 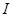 = «Некоторые селедки – рыбы»;
= «Некоторые селедки – рыбы»; 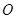 = «Некоторые селедки не являются рыбами».
= «Некоторые селедки не являются рыбами».
На основе правил преобразования высказываний и зависимостей между кванторами можно записать: 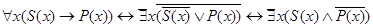 . Аналогично преобразуются и другие типы высказываний, в результате чего получаем зависимости:
. Аналогично преобразуются и другие типы высказываний, в результате чего получаем зависимости:
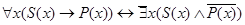 ;
;
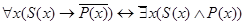 ;
;
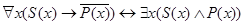 ;
;
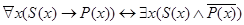 .
.
Как видно из приведенных равносильностей, высказывания 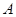 и
и 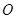 , а также
, а также 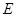 и
и 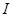 являются отрицаниями друг от друга (если одно из них истинно, то другое ложно и обратно) и называются противоположными. Из коммутативности операции конъюнкции следует, что суждения
являются отрицаниями друг от друга (если одно из них истинно, то другое ложно и обратно) и называются противоположными. Из коммутативности операции конъюнкции следует, что суждения 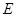 и
и 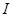 допускают перестановку предикатов, т. е.
допускают перестановку предикатов, т. е.
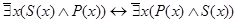 ;
;
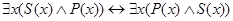 .
.
Приняв одно из категорических высказываний в качестве посылки, а другое – в качестве следствия, можно построить так называемые непосредственные заключения. Истинность или ложность заключения зависит только от его формы.
Обычно категорические высказывания сокращенно обозначают совокупностью трех букв 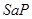 ,
, 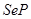 ,
, 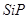 ,
, 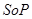 , где
, где 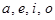 указывают на тип высказывания (
указывают на тип высказывания ( 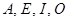 );
); 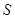 и
и  – термины, означающие свойства в таком порядке, в каком они входят в высказывание. Например, непосредственное заключение
– термины, означающие свойства в таком порядке, в каком они входят в высказывание. Например, непосредственное заключение 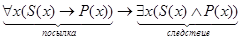 в принятых обозначениях запишется как
в принятых обозначениях запишется как 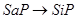 .
.
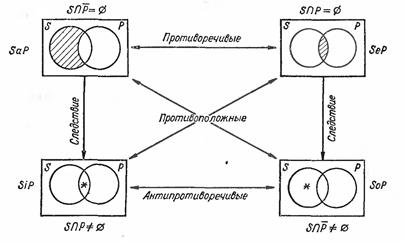
Традиционная схема отношений между категорическими высказываниями, называемая логическим квадратом, показана на рис. 18.
|
| Рис. 18 |
Там же приведены диаграммы Венна для каждого из четырех типов высказываний. Они непосредственно вытекают из правых частей выражений в (4) и теоретико-множественной интерпретации логических операций над предикатами, причем заштрихованные области соответствуют пустым множествам, а отмеченные звездочкой – непустым множествам. Так как 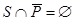 , если и только если
, если и только если 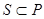 , то высказывание
, то высказывание 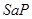 соответствует отношению включения множеств
соответствует отношению включения множеств 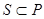 . В случае высказывания
. В случае высказывания 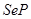 множества
множества 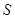 и
и  являются непересекающимися, а в случае высказывания
являются непересекающимися, а в случае высказывания 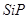 множества
множества 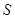 и
и  должны иметь непустую общую часть. Наконец, высказывание
должны иметь непустую общую часть. Наконец, высказывание 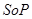 в силу тождества
в силу тождества 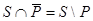 соответствует дополнению
соответствует дополнению 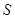 до
до  .
.
Особый интерес представляют общезначимые формулы, которые истинны (принимают значения 1) при каждом приписывании значений входящих в них свободных переменных и предикатов. Если 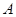 – общезначимая формула, то она, как и тавтологии, обозначается
– общезначимая формула, то она, как и тавтологии, обозначается 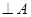 .
.
Для доказательства общезначимости формул используется аппарат логики высказываний, дополненный теоремами для выражений, содержащих кванторы. Приведем некоторые из них.
1) Пусть 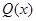 – формула, свободная для
– формула, свободная для 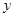 , тогда:
, тогда:
а) 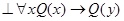 ; б)
; б) 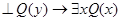 ;
;
2) Пусть 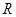 – формула, не содержащая свободных вхождений переменной
– формула, не содержащая свободных вхождений переменной  , и
, и 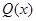 – какая-либо формула; тогда:
– какая-либо формула; тогда:
а) если 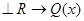 , то
, то 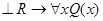 ; б) если
; б) если 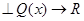 , то
, то 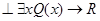 .
.
3) 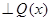 , если и только если
, если и только если 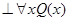 (следствие из теорем 1 и 2).
(следствие из теорем 1 и 2).
На основе этих теорем строятся правила вывода, которые, наряду с правилами исчисления высказываний (правила подстановки и заключения, теорема дедукции и др.), используются для доказательства логических следствий.
Правило универсальной конкретизации (УК): из 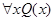 , которая свободна для
, которая свободна для 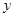 , выводится
, выводится 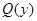 подстановкой в
подстановкой в 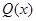 вместо
вместо  переменной
переменной 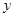 (теорема 1а).
(теорема 1а).
Правило универсального обобщения (УО): если 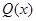 – следствие посылок, ни одна из которых не имеет свободных вхождений
– следствие посылок, ни одна из которых не имеет свободных вхождений  , то из нее выводится
, то из нее выводится 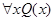 (теорема 2а).
(теорема 2а).
Кроме того, можно использовать еще два правила, представляющие собой аналоги приведенных выше правил для квантора существования.
Правило экзистенциальной конкретизации (ЭК) позволяет перейти от 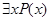 к
к 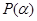 , где
, где 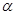 – неизвестный, но вполне определенный элемент такой, что, если
– неизвестный, но вполне определенный элемент такой, что, если 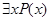 истинно, то
истинно, то 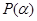 также истинно.
также истинно.
Правило экзистенциального обобщения (ЭО) позволяет перейти от 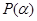 к
к 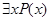 , т. е., если существует такое
, т. е., если существует такое 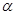 , что
, что 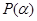 истинно, то истинно и
истинно, то истинно и 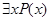 .
.
В логику предикатов полностью переносятся все тавтологии, в частности соотношения: а) 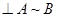 , если и только если
, если и только если 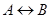 ; б)
; б) 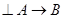 , если и только если
, если и только если 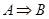 .
.
Исходя из понятия общезначимости, можно дать следующее определение логического следствия в логике предикатов: формула  есть логическое следствие формул
есть логическое следствие формул 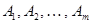 , т. е.
, т. е. 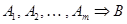 если для каждого множества определения и для каждого приписывания формулам
если для каждого множества определения и для каждого приписывания формулам 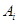 в этом множестве формула
в этом множестве формула  истинна при условии, что все
истинна при условии, что все 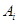 истинны. При этом для всех свободных вхождений некоторой переменной
истинны. При этом для всех свободных вхождений некоторой переменной  в какие-нибудь
в какие-нибудь 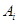 выбирается одно и то же значение
выбирается одно и то же значение  из множества определения, т. е. такое
из множества определения, т. е. такое  по существу рассматривают как постоянную.
по существу рассматривают как постоянную.
Рассмотрим пример. Сформулируем сложное высказывание, выраженное на обычном языке: «Некоторые студенты выполнили все задания. Ни один студент не выполнял графиков. Следовательно, ни одно задание не являлось графиком». В первом предложении участвуют одноместные предикаты – свойства 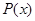 = «
= «  – студент»,
– студент», 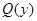 = «
= « 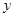 – задание» и двуместный предикат
– задание» и двуместный предикат 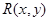 = «
= «  выполнил
выполнил 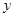 ». Так как в нем говорится о «некоторых студентах», то соответствующая форма будет
». Так как в нем говорится о «некоторых студентах», то соответствующая форма будет 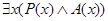 , где
, где 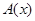 – сложное высказывание, характеризующее предикат
– сложное высказывание, характеризующее предикат 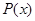 , а именно: «выполнили все задания». Поскольку речь идет о «всех заданиях», то переменная
, а именно: «выполнили все задания». Поскольку речь идет о «всех заданиях», то переменная 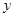 связывается квантором общности и высказывание
связывается квантором общности и высказывание 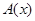 представляется формулой
представляется формулой 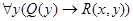 , которая дословно переводится «для всякого
, которая дословно переводится «для всякого 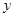 , если
, если 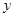 – задание, то
– задание, то  выполнили
выполнили 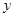 », смысл которого соответствует фразе «выполнили все задания». Итак, символическая запись первого предложения имеет вид:
», смысл которого соответствует фразе «выполнили все задания». Итак, символическая запись первого предложения имеет вид: 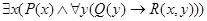 . Аналогично записывается и второе предложение
. Аналогично записывается и второе предложение 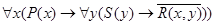 , где
, где 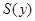 = «
= « 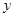 – график». Заключение «Ни одно задание не являлось графиком» представляет собой категорическое высказывание типа
– график». Заключение «Ни одно задание не являлось графиком» представляет собой категорическое высказывание типа 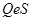 :
: 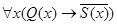 .
.
Таким образом, 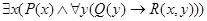 и
и 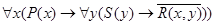 – посылки, а
– посылки, а 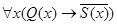 – заключение. Процесс доказательства представляется диаграммой вывода, приведенной на рис. 19. Применение правил вывода, специфических для логики предикатов, указано их сокращенными обозначениями. Остальные правила заимствованы из логики высказываний.
– заключение. Процесс доказательства представляется диаграммой вывода, приведенной на рис. 19. Применение правил вывода, специфических для логики предикатов, указано их сокращенными обозначениями. Остальные правила заимствованы из логики высказываний.
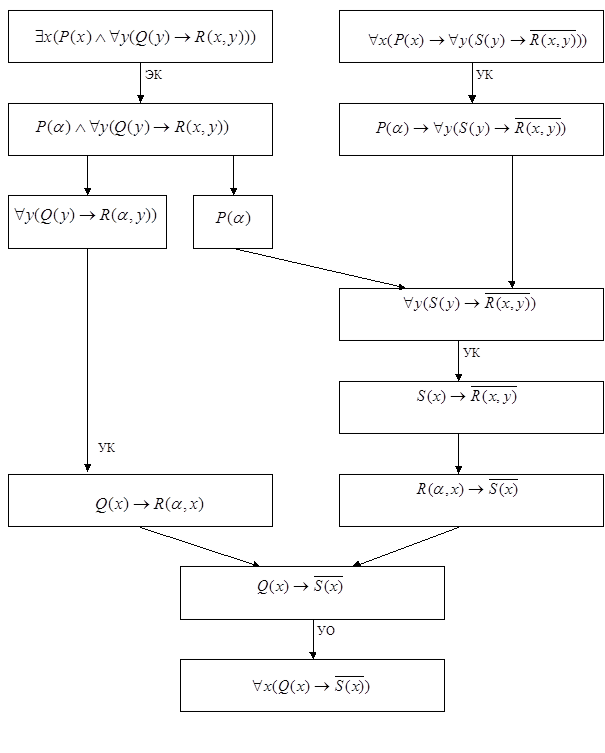
|
| Рис. 19 |
Дата добавления: 2016-09-06; просмотров: 3830;











