Глава 3. Алгебра высказываний
Пусть 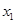 и
и 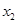 – некоторые высказывания, которые могут быть истинными (1) или ложными (0), например: «Я пойду в театр» (
– некоторые высказывания, которые могут быть истинными (1) или ложными (0), например: «Я пойду в театр» ( 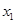 ) и «Я встречу друга» (
) и «Я встречу друга» ( 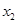 ). Дизъюнкцией
). Дизъюнкцией 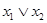 является сложное высказывание «Я пойду в театр или встречу друга», а конъюнкцией
является сложное высказывание «Я пойду в театр или встречу друга», а конъюнкцией 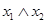 – высказывание «Я пойду в театр и встречу друга». Ясно, что если высказывание истинно, то его отрицание ложно. Сложное высказывание, образованное дизъюнкцией двух высказываний, истинно при условии, что истинно хотя бы одно из них. Сложное высказывание, образованное конъюнкцией двух истинных высказываний истинно, если истинны оба эти высказывания одновременно. Итак, высказывания можно рассматривать как двоичные переменные, а связки «не», «или», «и», с помощью которых образуются сложные высказывания, – как операции над этими переменными. В алгебре высказываний используются еще две операции: импликация
– высказывание «Я пойду в театр и встречу друга». Ясно, что если высказывание истинно, то его отрицание ложно. Сложное высказывание, образованное дизъюнкцией двух высказываний, истинно при условии, что истинно хотя бы одно из них. Сложное высказывание, образованное конъюнкцией двух истинных высказываний истинно, если истинны оба эти высказывания одновременно. Итак, высказывания можно рассматривать как двоичные переменные, а связки «не», «или», «и», с помощью которых образуются сложные высказывания, – как операции над этими переменными. В алгебре высказываний используются еще две операции: импликация 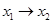 , соответствующая связке «если, то» и эквивалентность
, соответствующая связке «если, то» и эквивалентность 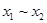 , соответствующая связке «если и только если» (2., табл. 1).
, соответствующая связке «если и только если» (2., табл. 1).
В нашем примере импликацией будет высказывание: «Если я пойду в театр, то встречу друга», а эквивалентностью – «Я пойду в театр, если и только если встречу друга». Импликация высказываний ложна только в случае, когда первое из простых высказываний истинно, а второе ложно. Эквивалентность является истинным высказыванием, если оба простые высказывания истинны или ложны одновременно. Обозначив буквами простые высказывания, можно представить сложное высказывание формулой с помощью соответствующих связок. Например, высказыванию «Если давление масла на шарик клапана больше усилия его пружины ( 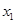 ), то масло открывает клапан (
), то масло открывает клапан ( 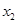 ) и частично перетекает из нагнетательной полости во впускную (
) и частично перетекает из нагнетательной полости во впускную ( 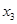 )» соответствует формула
)» соответствует формула 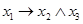 .
.
Рассматривая высказывания как двоичные переменные, обычно считают, что они удовлетворяют закону исключения третьего: каждое высказывание может быть истинным или ложным (третьего не дано). При этом высказывание не может быть одновременно и истинным и ложным (закон противоречия). Принятие закона исключения третьего позволяет полностью использовать в логике высказываний аппарат двузначной логики.
Слова «не», «и», «или», «если..., то» и «если и только если», с помощью которых в обычном языке из простых предложений образуются сложные предложения, называют сентенциональными связками. Каждой из этих связок соответствует своя логическая операция: отрицание, конъюнкция, дизъюнкция, импликация и эквивалентность. Обычно высказывания обозначают прописными буквами, а для операций используются те же символы, что и в алгебре логики. Таблицы соответствия в логике высказываний называют истинностными таблицами. Для указанных пяти связок они имеют вид:

| ||||

| ||||
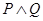
| ||||
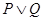
| ||||
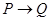
| ||||
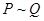
| ||||
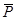
|
Истолкование отрицания 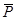 , конъюнкции
, конъюнкции 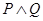 и дизъюнкции
и дизъюнкции 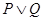 обычно не вызывает трудностей. Импликации
обычно не вызывает трудностей. Импликации 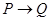 в обычной речи соответствует условное предложение «если
в обычной речи соответствует условное предложение «если  , то
, то  », причем
», причем  называется посылкой (антецедентом), a
называется посылкой (антецедентом), a  – следствием (консеквентом). Могут встретиться и другие выражения, имеющие тот же тип логической связи, например: «
– следствием (консеквентом). Могут встретиться и другие выражения, имеющие тот же тип логической связи, например: «  влечет
влечет  », «
», «  только тогда, когда
только тогда, когда  », «
», «  есть достаточное условие для
есть достаточное условие для  », «
», «  при условии, что
при условии, что  », «
», «  есть необходимое условие для
есть необходимое условие для  » и т. п. Эквивалентность
» и т. п. Эквивалентность 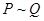 определяет логическую связь в так называемых биусловных предложениях типа «
определяет логическую связь в так называемых биусловных предложениях типа «  , если и только если
, если и только если  » или в других грамматических формах: «
» или в других грамматических формах: «  тогда и только тогда, когда
тогда и только тогда, когда  », «если
», «если  , то
, то  и обратно, если
и обратно, если  , то
, то  », «
», «  есть необходимое и достаточное условие для
есть необходимое и достаточное условие для  ».
».
Всякое сложное предложение, которое состоит из простых предложений, связанных сентенциональными связками, можно представить в символической форме. В результате получаем высказывательную формулу. На каждом наборе значений истинности букв (переменных) формула принимает некоторое значение. Следовательно, всякую формулу логики высказываний можно рассматривать как истинностную функцию. Рассмотрим, например, сложное высказывание: «Если применить стальные конструкции (  ), то масса снижается (
), то масса снижается (  ) и стоимость увеличивается (
) и стоимость увеличивается ( 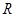 ). Стальные конструкции не применяются (
). Стальные конструкции не применяются ( 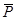 ), а масса снижается (
), а масса снижается (  )». Соответствующая формула
)». Соответствующая формула 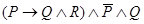 представляется следующей таблицей истинности:
представляется следующей таблицей истинности:

| ||||||||

| ||||||||
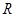
| ||||||||
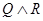
| ||||||||
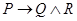
| ||||||||
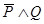
| ||||||||
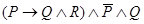
|
Отсюда видно, что сложное предложение истинно на двух наборах значений аргументов  ,
,  ,
, 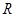 , а именно: (0, 1, 0) и (0, 1, 1), а на остальных наборах оно ложно.
, а именно: (0, 1, 0) и (0, 1, 1), а на остальных наборах оно ложно.
В логике высказываний дается следующее определение формулы:
1) переменные высказывания суть формулы;
2) если 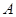 и
и 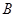 – формулы, то (
– формулы, то ( 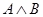 ), (
), ( 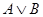 ), (
), ( 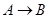 ), (
), ( 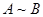 ) и
) и 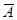 также формулы. Это определение имеет рекурсивный характер в том смысле, что первая его часть определяет элементарные формулы, а вторая позволяет из любых формул образовать новые формулы. Пусть, например, требуется получить формулу
также формулы. Это определение имеет рекурсивный характер в том смысле, что первая его часть определяет элементарные формулы, а вторая позволяет из любых формул образовать новые формулы. Пусть, например, требуется получить формулу 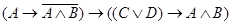 . Выбираем необходимое множество элементарных формул
. Выбираем необходимое множество элементарных формул 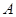 ,
, 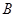 ,
, 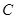 ,
, 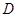 . Затем последовательно получаем формулы
. Затем последовательно получаем формулы 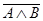 ,
, 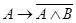 ,
, 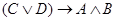 ,
, 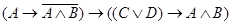 . Как видно, процесс образования формулы происходит путем расширения их множества до тех пор, пока это множество не будет содержать требуемую формулу. Все формулы, построенные в указанном процессе, называются частями результирующей формулы.
. Как видно, процесс образования формулы происходит путем расширения их множества до тех пор, пока это множество не будет содержать требуемую формулу. Все формулы, построенные в указанном процессе, называются частями результирующей формулы.
Если имеется некоторая высказывательная формула, то можно построить соответствующее сложное предложение, заменяя буквы простыми предложениями (одинаковые вхождения букв замещаются одним и тем же предложением). Полученное таким путем предложение называется подстановкой в данную формулу. Так, полагая  – «идет снег»,
– «идет снег»,  – «2 ´ 2 = 4» и
– «2 ´ 2 = 4» и 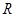 – «слоны зеленые», по формуле
– «слоны зеленые», по формуле 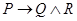 получаем подстановку: «Если идет снег, то 2 ´ 2 = 4 и слоны зеленые». Истинность этого высказывания определяется только приведенной выше таблицей и никоим образом не связана с конкретным содержанием как простых предложений, так и полученного в результате их объединения сложного предложения. Как видно из таблицы, истинностная функция истинна на всех наборах значений аргументов, кроме наборов {1,0,0}, {1,0, 1} и {1, 1, 0}. Например, при
получаем подстановку: «Если идет снег, то 2 ´ 2 = 4 и слоны зеленые». Истинность этого высказывания определяется только приведенной выше таблицей и никоим образом не связана с конкретным содержанием как простых предложений, так и полученного в результате их объединения сложного предложения. Как видно из таблицы, истинностная функция истинна на всех наборах значений аргументов, кроме наборов {1,0,0}, {1,0, 1} и {1, 1, 0}. Например, при 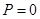 ,
, 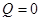 и
и 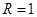 , получим истинное высказывание: «Если не идет снег, то 2 ´ 2 ¹ 4 и слоны зеленые».
, получим истинное высказывание: «Если не идет снег, то 2 ´ 2 ¹ 4 и слоны зеленые».
С точки зрения «здравого смысла» такие высказывания кажутся несуразными, и возможность их появления в логике высказываний следовало бы исключить. Однако необходимо преодолеть психологический барьер и понять, что ограничения, основанные на «здравом смысле» и причинной связи в логике высказывании не только невозможны, но и нежелательны. Логика высказываний отвлекается от конкретного содержания высказываний и занимается лишь анализом и синтезом высказывательных формул и изучением отношений между высказываниями. Что же касается «здравого смысла», то он должен проявляться при использовании законов логики высказываний в ее конкретных приложениях.
Тождественно истинная формула, т. е. такая формула, которая принимает значения 1 при любых значениях ее компонентов, называется тавтологией. Тождественно ложная формула на всех наборах ее компонентов принимает значение 0 и называется противоречием. Если в технических приложениях логические функции, выражаемые тавтологиями или противоречиями, практически не представляют интереса, то в логике высказываний они играют первостепенную роль. Примером тавтологии может служить высказывание: «Если внедрить новую технологию (  ), то качество продукции улучшится (
), то качество продукции улучшится (  ). При улучшении качества продукции (
). При улучшении качества продукции (  ), ее сбыт увеличивается (
), ее сбыт увеличивается ( 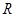 ). Новая технология внедрена (
). Новая технология внедрена (  ). Следовательно, сбыт продукции увеличился (
). Следовательно, сбыт продукции увеличился ( 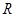 )». Оно выражается формулой
)». Оно выражается формулой 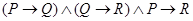 .Чтобы выяснить, является ли данная формула тавтологией, можно составить для нее истинностную таблицу. Так, для приведенной выше формулы имеем:
.Чтобы выяснить, является ли данная формула тавтологией, можно составить для нее истинностную таблицу. Так, для приведенной выше формулы имеем:

| ||||||||

| ||||||||
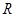
| ||||||||
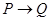
| ||||||||
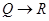
| ||||||||
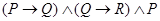
| ||||||||
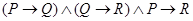
|
Можно также воспользоваться зависимостями, приведенными в (2) и преобразовать высказывательную формулу к нормальной форме. Если хотя бы один член дизъюнктивной нормальной формы окажется равным 1, то соответствующая ей формула является тавтологией. Если хотя бы один член конъюнктивной нормальной формы окажется равным 0, то соответствующая ей формула является противоречием. Очевидно, формула не является тавтологией, если она принимает значение 0 хотя бы на одном наборе значений переменных. Этим обстоятельством можно воспользоваться для распознавания тавтологий сокращенным методом «обратного рассуждения», заключающемся в поиске таких переменных, при которых формула оказывается ложной. Так, приведенная выше формула может принять значение 0, если и только если 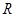 ложно, а
ложно, а 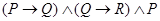 истинно. При этом должны быть истинны
истинно. При этом должны быть истинны 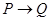 ,
, 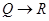 и
и  . При истинном
. При истинном  формула
формула 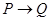 истинна только при истинном
истинна только при истинном  . В свою очередь, при истинном
. В свою очередь, при истинном  формула
формула 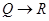 истинна только при истинном
истинна только при истинном 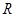 . Таким образом, анализируемая формула может быть ложной, если и только если
. Таким образом, анализируемая формула может быть ложной, если и только если 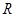 одновременно и истинно и ложно, что невозможно в силу закона противоречия. Следовательно, она является тавтологией. Для указания на то, что данная формула является тавтологией, используется знак
одновременно и истинно и ложно, что невозможно в силу закона противоречия. Следовательно, она является тавтологией. Для указания на то, что данная формула является тавтологией, используется знак 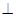 , который помещается перед формулой, например:
, который помещается перед формулой, например: 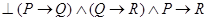 .
.
Различные подстановки в тавтологию, независимо от их конкретного содержания, всегда являются истинными предложениями в силу одной только своей логической структуры. Иначе говоря, тавтологии можно рассматривать как некоторые логически истинные схемы рассуждений или утверждений. Поэтому они играют роль законов (теорем) логики высказываний, претендующих на установление методов построения правильных умозаключений. Существует бесконечное множество тавтологий, а значит, и законов логики высказываний. Наиболее часто используемые из них следующие: 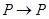 (закон тождества),
(закон тождества), 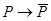 (закон исключения третьего),
(закон исключения третьего), 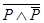 (закон противоречия),
(закон противоречия), 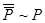 (закон двойного отрицания),
(закон двойного отрицания), 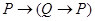 (добавление антецедента – истина из чего угодно),
(добавление антецедента – истина из чего угодно), 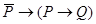 (из ложного что угодно),
(из ложного что угодно), 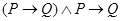 (закон отделения),
(закон отделения), 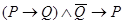 (modus tollens),
(modus tollens), 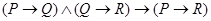 (закон силлогизма),
(закон силлогизма), 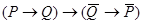 (закон контрапозиции).
(закон контрапозиции).
Каждый из законов логики высказываний отображает в символической форме некоторую схему доказательства. Например, в соответствии с законом отделения, если истинно, что некоторое высказывание  имплицирует высказывание
имплицирует высказывание 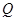 и, кроме того,
и, кроме того,  истинно, то истинно и
истинно, то истинно и 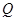 . Modus tollens применяется при доказательстве от противного: желая доказать утверждение
. Modus tollens применяется при доказательстве от противного: желая доказать утверждение  , предполагается, что
, предполагается, что  ложно, и показывается, что
ложно, и показывается, что  имплицирует некоторое высказывание
имплицирует некоторое высказывание 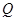 , о котором известно, что оно ложно (
, о котором известно, что оно ложно ( 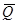 истинно). Отсюда заключается, что
истинно). Отсюда заключается, что  истинно.
истинно.
Две формулы называются равносильными, если на всех наборах значений входящих в них переменных эти формулы принимают одинаковые значения. Для обозначения этого отношения часто употребляют символ 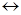 , так что равносильность формул
, так что равносильность формул 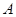 и
и  символически записывается как
символически записывается как 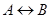 . Легко видеть, что равносильность – это отношение эквивалентности: оно рефлексивно (
. Легко видеть, что равносильность – это отношение эквивалентности: оно рефлексивно ( 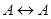 ), симметрично (если
), симметрично (если 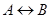 , то
, то 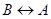 ) и транзитивно (из
) и транзитивно (из 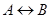 и
и 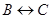 следует, что
следует, что 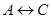 ). Поэтому равносильность называют также логической эквивалентностью.
). Поэтому равносильность называют также логической эквивалентностью.
Равносильность формул логики высказываний вытекает из тождественности соответствующих формул алгебры логики, из которых можно получить следующие равносильности: 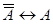 ;
; 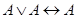 ;
; 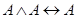 ;
; 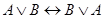 ;
; 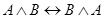 ;
; 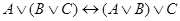 ;
; 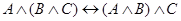 ;
; 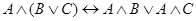 ;
; 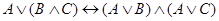 ;
; 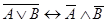 ;
; 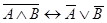 и т. д. Кроме того, с помощью отношения равносильности выражаются различные связки между формулами:
и т. д. Кроме того, с помощью отношения равносильности выражаются различные связки между формулами: 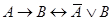 ;
; 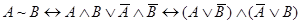 ;
; 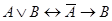 ;
; 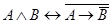 ;
; 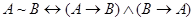 . Эти и подобные им равносильные соотношения можно использовать для преобразования и упрощения структуры сложного высказывания. Так, для приведенного ранее примера
. Эти и подобные им равносильные соотношения можно использовать для преобразования и упрощения структуры сложного высказывания. Так, для приведенного ранее примера 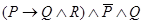 имеем:
имеем:
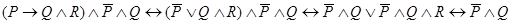 .
.
Между отношением равносильности и эквивалентностью формул существует следующая связь: если 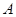 и
и  – равносильны, то
– равносильны, то 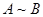 – тавтология, и обратно, если
– тавтология, и обратно, если 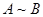 – тавтология, то
– тавтология, то 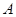 и
и  – равносильны. Это сокращенно записывается так:
– равносильны. Это сокращенно записывается так: 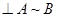 , если и только если
, если и только если 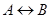 .
.
Из изложенного ясно, что тавтологии можно получить из равносильности заменой знака 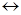 на знак ~.
на знак ~.
Говорят, что формула  является логическим следствием формулы
является логическим следствием формулы 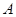 и пишут
и пишут 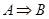 , если
, если  истинно на всех наборах значений переменных, для которых
истинно на всех наборах значений переменных, для которых 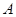 истинно. Легко убедиться, что
истинно. Легко убедиться, что 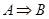 , если и только если
, если и только если 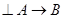 . Действительно, в соответствии с определением импликации
. Действительно, в соответствии с определением импликации 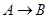 ложно только при истинном
ложно только при истинном 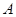 и ложном
и ложном  и, следовательно, если
и, следовательно, если 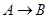 – тавтология, то из истинности
– тавтология, то из истинности 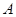 всегда следует истинность
всегда следует истинность  , т. е.
, т. е. 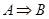 . Обратно, если
. Обратно, если 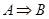 , то исключается случай, когда
, то исключается случай, когда 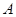 истинно и
истинно и  ложно, а значит
ложно, а значит 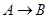 истинно на всех наборах значений переменных, т. е.
истинно на всех наборах значений переменных, т. е. 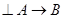 .
.
Логическое следствие 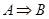 означает, что из истинности
означает, что из истинности 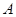 следует истинность
следует истинность  , но если
, но если 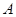 ложно, то относительно
ложно, то относительно  ничего утверждать нельзя. Это отношение обобщается на совокупность высказываний:
ничего утверждать нельзя. Это отношение обобщается на совокупность высказываний:  есть логическое следствие высказываний
есть логическое следствие высказываний 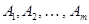 , если из истинности всех
, если из истинности всех 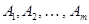 следует истинность
следует истинность  . Из определения конъюнкции можно заключить, что это сводится к соотношению
. Из определения конъюнкции можно заключить, что это сводится к соотношению 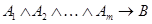 , необходимым и достаточным условием которого является тавтология
, необходимым и достаточным условием которого является тавтология 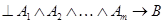 .
.
Пусть, например, даны высказывания 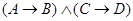 ;
; 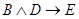 ;
; 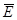 и необходимо установить, является ли высказывание
и необходимо установить, является ли высказывание 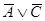 логическим следствием. Это сводится к доказательству тавтологии
логическим следствием. Это сводится к доказательству тавтологии 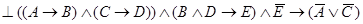 . Воспользовавшись методом «обратного рассуждения», положим, что следствие
. Воспользовавшись методом «обратного рассуждения», положим, что следствие 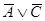 ложно (
ложно ( 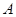 и
и 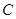 истинны) при истинном значении всех посылок. Тогда, как следует из первой посылки,
истинны) при истинном значении всех посылок. Тогда, как следует из первой посылки,  и
и 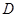 должны быть истинны, а из истинности
должны быть истинны, а из истинности 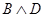 и второй посылки следует истинность
и второй посылки следует истинность 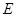 . Но это противоречит третьей посылке
. Но это противоречит третьей посылке 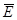 , что и доказывает данную тавтологию.
, что и доказывает данную тавтологию.
Между логическим следствием и логической эквивалентностью имеется связь, которая вытекает из соотношения 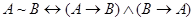 , приведенного ранее. Оно означает:
, приведенного ранее. Оно означает: 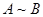 , если и только если
, если и только если 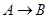 и
и 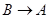 . Пусть
. Пусть 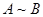 – тавтология, тогда
– тавтология, тогда 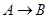 и
и 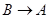 – также тавтологии, т. е.
– также тавтологии, т. е. 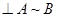 , если и только если
, если и только если 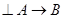 и
и 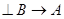 . А это равносильно утверждению:
. А это равносильно утверждению: 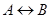 , если и только если
, если и только если 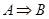 и
и 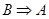 .
.
Логическое следствие есть отношение порядка; так, оно рефлексивно ( 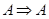 ), транзитивно (если
), транзитивно (если 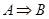 и
и 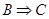 , то
, то 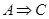 ) и антисимметрично (из
) и антисимметрично (из 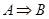 и
и 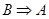 следует
следует 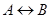 ).
).
Формальная теория вывода ставит своей главной задачей образование из некоторой совокупности исходных тавтологий новых формул, которые также являются тавтологиями. Эта задача решается с помощью правил вывода:
1) если 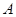 – тавтология, то, заменяя в ней букву
– тавтология, то, заменяя в ней букву 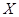 всюду, где она входит, произвольной формулой
всюду, где она входит, произвольной формулой  , получаем также тавтологию (правило подстановки);
, получаем также тавтологию (правило подстановки);
2) если 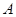 и
и 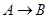 суть тавтологии, то
суть тавтологии, то  – также тавтология (правило заключения).
– также тавтология (правило заключения).
Первое из этих правил почти очевидно, а второе непосредственно следует из закона отделения 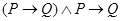 .
.
Формула называется выводимой в исчислении высказываний, если она может быть получена из конечной совокупности исходных формул путем конечного числа шагов применения правил вывода. Вообще говоря, не все тождественно истинные формулы могут быть выведены из произвольного множества тавтологий. В то же время строго доказано, что можно выбрать такую конечную совокупность исходных тавтологий (аксиом исчисления высказываний), из которой выводимы все тождественно истинные формулы. Это важное положение решает проблему полноты исчисления высказываний. Предложено много различных систем аксиом исчисления высказываний. Одна из них включает следующие тавтологии:
1) 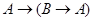 ;
;
2) 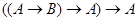 ;
;
3) 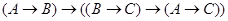 ;
;
4) 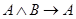 ;
;
5) 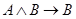 ;
;
6) 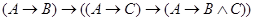 ;
;
7) 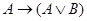 ;
;
8) 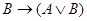 ;
;
9) 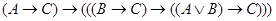 ;
;
10) 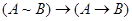 ;
;
11) 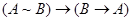 ;
;
12) 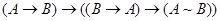 ;
;
13) 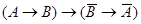 ;
;
14) 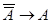 ;
;
15) 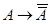 .
.
Выведем, например, тавтологию 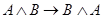 . Подстановка в аксиому 6 вместо
. Подстановка в аксиому 6 вместо 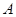 формулы
формулы 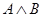 дает
дает 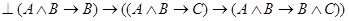 , что после подстановки
, что после подстановки 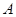 вместо
вместо 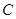 приводится к
приводится к 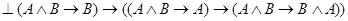 . Посылка в этой формуле есть аксиома 5, поэтому на основе правила заключения
. Посылка в этой формуле есть аксиома 5, поэтому на основе правила заключения 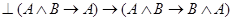 . Так как посылка в полученной тавтологии является аксиомой 4, то, применяя еще раз правило заключения, получаем
. Так как посылка в полученной тавтологии является аксиомой 4, то, применяя еще раз правило заключения, получаем 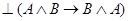 , что и требовалось доказать.
, что и требовалось доказать.
Формализация процесса вывода имеет большое теоретическое значение и позволяет построить схему доказательства, которая может быть реализована на вычислительных машинах. Однако сложность аксиоматического подхода к выводу тавтологий заставляет искать и применять специальные правила, которые сокращают многократное применение основных правил вывода.
Более краткий и простой способ вывода основан на теореме дедукции: если формула  является логическим следствием формул
является логическим следствием формул 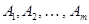 , т. е.
, т. е. 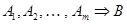 , то
, то 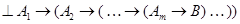 . При этом говорят, что формула
. При этом говорят, что формула  выводима из формул
выводима из формул 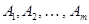 .
.
Из теоремы дедукции и определения логического следствия вытекают следующие положения:
1) 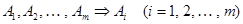 , т. е. любая из совокупности посылок является логическим следствием этой совокупности;
, т. е. любая из совокупности посылок является логическим следствием этой совокупности;
2) если 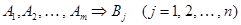 и
и 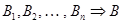 , то
, то 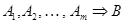 .
.
С помощью этих правил можно представить доказательство того, что формула  есть логическое следствие формул
есть логическое следствие формул 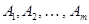 в виде цепочки формул, последней из которых является
в виде цепочки формул, последней из которых является  . Промежуточные формулы
. Промежуточные формулы 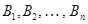 получаются на основании известных логических законов, аксиом и эквивалентностей. На основе теоремы дедукции используемые тавтологии и результирующее соотношение преобразуются к требуемой форме.
получаются на основании известных логических законов, аксиом и эквивалентностей. На основе теоремы дедукции используемые тавтологии и результирующее соотношение преобразуются к требуемой форме.
В качестве примера докажем, что 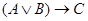 ;
; 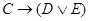 ;
; 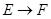 ;
; 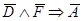 . Из первой пары посылок на основе закона силлогизма получаем
. Из первой пары посылок на основе закона силлогизма получаем 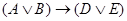 . Из последней посылки следует
. Из последней посылки следует 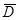 и
и 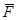 . Из посылки
. Из посылки 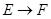 и
и 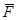 выводим (modus tollens)
выводим (modus tollens) 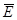 . Из
. Из 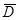 и
и 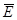 получаем
получаем 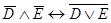 , что совместно с
, что совместно с 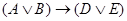 в соответствии с modus tollens дает
в соответствии с modus tollens дает 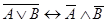 , откуда выводим
, откуда выводим 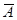 . Наглядно этот процесс вывода изображается диаграммой, показанной на рис. 17.
. Наглядно этот процесс вывода изображается диаграммой, показанной на рис. 17.
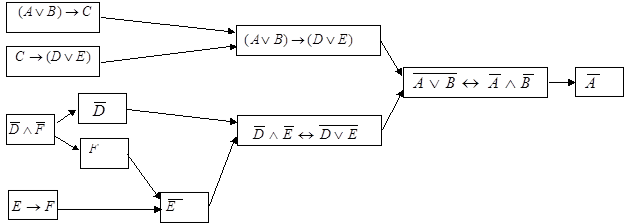
|
| Рис. 17. |
Если в качестве логического следствия выводится конъюнкция некоторого высказывания и его отрицания 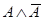 , то это свидетельствует о противоречивости посылок (из нее выводится произвольное высказывание, как истинное, так и ложное).
, то это свидетельствует о противоречивости посылок (из нее выводится произвольное высказывание, как истинное, так и ложное).
Контрольные вопросы к лекции 6
6-1. Что называется сентенциональными связками в логике высказываний?
6-2. Какой сентенциональной связке в логике высказываний соответствует логическая операция отрицания?
6-3. Какой сентенциональной связке в логике высказываний соответствует логическая операция дизъюнкции?
6-4. Какой сентенциональной связке в логике высказываний соответствует логическая операция конъюнкции?
6-5. Какой сентенциональной связке в логике высказываний соответствует логическая операция импликации?
6-6. Какой сентенциональной связке в логике высказываний соответствует логическая операция эквивалентности?
6-7. Что называется высказывательной формулой в логике высказываний?
6-8. Какая высказывательная формула называется тавтологией?
6-9. Какая высказывательная формула называется противоречием?
6-10. Как символически записывается закон тождества?
6-11. Как символически записывается закон исключения третьего?
6-12. Как символически записывается закон противоречия?
6-13. Как символически записывается закон двойного отрицания?
6-14. Как символически записывается закон добавления антецедента?
6-15. Как символически записывается закон отделения?
6-16. Как символически записывается закон силлогизма?
6-17. Как символически записывается закон контрапозиции?
6-18. Какие формулы называются равносильными?
6-19. Какая связь существует между отношением равносильности и эквивалентностью?
6-20. В каком случае одна формула является логическим следствием другой формулы?
6-21. В чем состоят правила вывода?
Дата добавления: 2016-09-06; просмотров: 2572;











