Глава 2. Конечные автоматы
Лекция 5. Конечные автоматы
В логических схемах, рассмотренных в предыдущем разделе, значения выходных переменных определяются только комбинацией значений переменных на входах в данный момент времени. Поэтому их называют комбинационными схемами. В общем случае выходные переменные могут зависеть от значений входных переменных не только в данный момент, но и от их предыдущих значений. Иначе говоря, значения выходных переменных определяются последовательностью значений входных переменных, в связи с чем схемы с такими свойствами называют последовательностными. Если входные и выходные переменные принимают значения из конечных алфавитов, то оба типа схем объединяются под названием конечные автоматы. Пусть 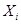 – алфавит входной переменной
– алфавит входной переменной 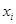 , a
, a 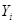 – алфавит выходной переменной
– алфавит выходной переменной 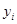 . Конечный автомат с
. Конечный автомат с 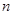 входами и
входами и 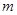 выходами характеризуется входным алфавитом
выходами характеризуется входным алфавитом 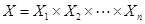 и выходным алфавитом
и выходным алфавитом 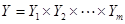 , причем символами входного алфавита служат слова
, причем символами входного алфавита служат слова 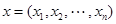 длины
длины 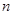 , а символами выходного алфавита – слова
, а символами выходного алфавита – слова 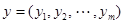 длины
длины 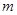 , где
, где 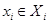 и
и 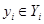 . Особого внимания заслуживают конечные автоматы с двузначным структурным алфавитом, зависимости между входными и выходными переменными которых выражаются булевыми функциями. Их значение обусловлено тем, что любая информация может быть представлена в двоичных кодах (двоично-десятичные коды чисел, телетайпный код в технике связи и т. п.). В то же время при технической реализации автоматов используются преимущественно двоичные элементы и двузначная логика. В реальных условиях сигналы представляются непрерывными функциями времени, поэтому для надежного различения сигналов требуется, чтобы новые значения на входах появлялись после окончания переходных процессов, связанных с предыдущими значениями. При рассмотрении логической структуры автоматов обычно отвлекаются от существа этих процессов и считают, что переменные изменяются не непрерывно, а мгновенно в некоторые моменты времени, называемые тактами. Интервалы между тактами могут быть различными, но без потери общности их можно считать равными
. Особого внимания заслуживают конечные автоматы с двузначным структурным алфавитом, зависимости между входными и выходными переменными которых выражаются булевыми функциями. Их значение обусловлено тем, что любая информация может быть представлена в двоичных кодах (двоично-десятичные коды чисел, телетайпный код в технике связи и т. п.). В то же время при технической реализации автоматов используются преимущественно двоичные элементы и двузначная логика. В реальных условиях сигналы представляются непрерывными функциями времени, поэтому для надежного различения сигналов требуется, чтобы новые значения на входах появлялись после окончания переходных процессов, связанных с предыдущими значениями. При рассмотрении логической структуры автоматов обычно отвлекаются от существа этих процессов и считают, что переменные изменяются не непрерывно, а мгновенно в некоторые моменты времени, называемые тактами. Интервалы между тактами могут быть различными, но без потери общности их можно считать равными 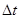 . Предполагается, что тактовые моменты
. Предполагается, что тактовые моменты 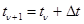 определяются синхронизирующими сигналами. Таким образом, вводится понятие дискретного автоматного времени
определяются синхронизирующими сигналами. Таким образом, вводится понятие дискретного автоматного времени 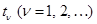 , причем переменные зависят не от физического времени, а от номера такта
, причем переменные зависят не от физического времени, а от номера такта 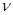 , т. е. вместо непрерывных функций
, т. е. вместо непрерывных функций 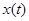 рассматриваются дискретные значения
рассматриваются дискретные значения 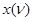 .
.
Кроме входных и выходных переменных, можно выделить некоторую совокупность промежуточных переменных, которые связаны с внутренней структурой автомата. В комбинационных схемах промежуточные переменные непосредственно не участвуют в соотношениях вход – выход. Напротив, выходные функции последовательностных схем в качестве своих аргументов, кроме входных переменных, обязательно содержат некоторую совокупность промежуточных переменных 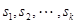 , характеризующих состояние схемы. Набор всех возможных состояний, которые присущи данной схеме, называется множеством состояний. Если
, характеризующих состояние схемы. Набор всех возможных состояний, которые присущи данной схеме, называется множеством состояний. Если 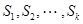 – конечные алфавиты переменных состояния
– конечные алфавиты переменных состояния 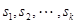 , то множество состояний
, то множество состояний 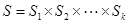 также является конечным множеством.
также является конечным множеством.
Строгое определение понятия состояния связывается с той ролью, которое оно играет при описании конечных автоматов. Во-первых, значения совокупности выходных переменных на 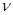 -м такте
-м такте 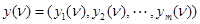 однозначно определяется значениями входных переменных
однозначно определяется значениями входных переменных 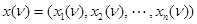 и состоянием
и состоянием 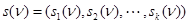 на том же такте, т. e.
на том же такте, т. e. 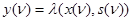 . Во-вторых, состояние
. Во-вторых, состояние 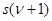 в следующем
в следующем 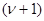 -м такте однозначно определяется входными переменными
-м такте однозначно определяется входными переменными 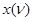 и состоянием
и состоянием 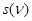 в предыдущем такте, т. е.
в предыдущем такте, т. е. 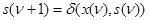 .
.
Таким образом, состояние конечного автомата в любой тактовый момент характеризуется значениями такой совокупности переменных, которая вместе с заданными значениями входных переменных позволяет определить выходные переменные в данный тактовый момент и состояние в следующий тактовый момент.
Ясно, что последовательностные схемы должны обладать способностью сохранять предыдущее состояние до следующего такта, в связи с чем их называют также автоматами с памятью. В качестве памяти могут использоваться элементы задержки, на выходах которых повторяются входные воздействия со сдвигом во времени на интервал между тактами 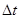 . Широко применяются также различные запоминающие элементы, например, триггеры, способные сохранять состояния на выходах до тех пор, пока оно не изменяется в результате воздействия на их входы.
. Широко применяются также различные запоминающие элементы, например, триггеры, способные сохранять состояния на выходах до тех пор, пока оно не изменяется в результате воздействия на их входы.
В технике с понятием автомата обычно связывается некоторое устройство, способное выполнять определенные функции без вмешательства человека или с его ограниченным участием. Однако такое понимание является слишком узким. В широком смысле конечный автомат – это математическая модель, отображающая физические или абстрактные явления самой разнообразной природы. Такая модель успешно используется как в технике (проектирование электронных вычислительных машин, систем управления и связи), так и в других областях – психологии и физиологии (исследование деятельности нервной системы человека и простейших видов поведения животных), лингвистике (анализ синтаксиса русского, английского или других языков, расшифровка древних рукописей), теории и практике административного управления и т. п. Универсальность теории автоматов позволяет рассматривать с единой точки зрения различные объекты, устанавливать связи и аналогии между ними, переносить результаты из одной области в другую.
Конечный автомат 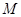 определяется как система с конечным входным алфавитом
определяется как система с конечным входным алфавитом 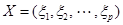 , конечным выходным алфавитом
, конечным выходным алфавитом 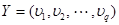 , конечным множеством состояний
, конечным множеством состояний 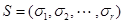 и двумя характеристическими функциями:
и двумя характеристическими функциями:
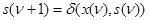 ;
;
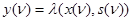 ,
,
называемыми соответственно функцией переходов и функцией выходов. Общая блок-схема конечного автомата (рис. 13) может быть представлена в виде комбинационной схемы, реализующей характеристические функции 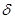 и
и 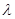 , и памяти, сохраняющей на один такт предыдущее состояние автомата.
, и памяти, сохраняющей на один такт предыдущее состояние автомата.
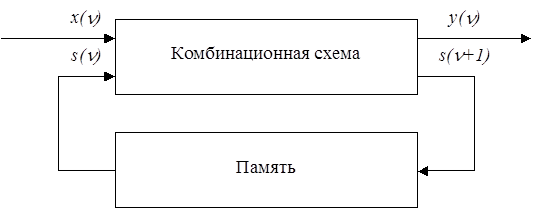
|
| Рис. 13. |
В определении автомата участвует три конечных множества 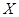 ,
, 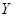 ,
, 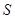 и две функции
и две функции 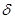 и
и 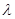 , задающие некоторые отношения между элементами этих множеств. Следовательно, конечный автомат можно обозначить упорядоченной пятеркой
, задающие некоторые отношения между элементами этих множеств. Следовательно, конечный автомат можно обозначить упорядоченной пятеркой 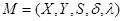 . Мощности множеств
. Мощности множеств 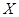 ,
, 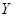 ,
, 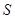 равны соответственно:
равны соответственно:
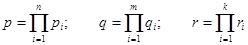 ,
,
где 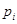 ,
, 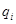 ,
, 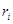 – количество символов в алфавитах входной переменной
– количество символов в алфавитах входной переменной 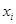 , выходной переменной
, выходной переменной 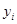 и переменной состояния
и переменной состояния 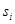 . При двоичном алфавите
. При двоичном алфавите 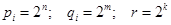 .
.
Приведенное определение автомата связывают обычно с автоматом первого рода, называемым также автоматом Мили. Если выходные переменные являются функцией только состояния, то имеем автомат второго рода или автомат Мура.
Автомат называется конечным, если конечны множества 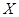 ,
, 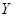 ,
, 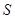 .
.
Автомат называется детерминированным, если в нем выполнено условие однозначности переходов: находясь в некотором состоянии, он не может перейти более, чем в одно состояние под действием одного и того же входного сигнала.
Автомат носит название инициального, если в нем выделено начальное состояние 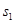 .
.
Автомат называется полностью определенным, если область определения функции переходов d совпадает с множеством всевозможных пар вида 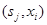 . Для автомата Мили область определения функции l также совпадает с множеством всевозможных пар вида
. Для автомата Мили область определения функции l также совпадает с множеством всевозможных пар вида 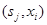 , а для автомата Мура – с множеством состояний
, а для автомата Мура – с множеством состояний 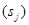 .
.
Автомат называется частичным, если либо функция d определена не на всех парах 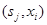 , либо функция l определена не на всех указанных парах для автомата Мили и на множестве не всех внутренних состояний для автомата Мура.
, либо функция l определена не на всех указанных парах для автомата Мили и на множестве не всех внутренних состояний для автомата Мура.
Среди многообразия различных способов задания автомата наибольшее распространение получили табличный и графический. В первом случае автомат Мили описывается в виде двух таблиц. Одна из них, называемая таблицей переходов, задает функцию d (табл. 5), вторая, называемая таблицей выходов, задает функцию l (табл. 6). Для приведенных таблиц определены множества S = {s1,s2,s3,s4}, X = {x1,x2}, Y = {y1,y2,y3,y4,y5}.
| Табл. 5 | Табл. 6 | Табл. 7 | ||||||||||||||
| s1 | s2 | s3 | s4 | s1 | s2 | s3 | s4 | s1 | s2 | s3 | s4 | |||||
| x1 | s2 | s2 | s1 | s1 | x1 | y1 | y1 | y2 | y4 | x1 | s2/y1 | s2/y1 | s1/y2 | s1/y4 | ||
| x2 | s4 | s3 | s4 | s3 | x2 | y5 | y3 | y4 | y5 | x2 | s4/y5 | s3/y3 | s4/y4 | s3/y5 |
Каждому столбцу обеих таблиц поставлено в соответствие одно состояние автомата из множества S, каждой строке – один входной сигнал из множества X. На пересечении столбца sj и строки xi в таблице переходов записывается состояние ss, в которое должен перейти автомат из состояния sj под действием входного сигнала xi, т.е. ss = d(sj, xi). На пересечении столбца sj и строки xi в таблице выходов записывается выходной сигнал yg, выдаваемый автоматом в состоянии sj при поступлении на вход сигнала xi, т.е. yg = l(sj, xi). Иногда пользуются одной совмещенной таблицей (табл. 7).
| Автомат Мура задается одной таблицей переходов (табл. 8), в которой каждому столбцу приписаны не только состояние sj, но и выходной сигнал yg, соответствующий этому состоянию, т.е. yg = l(sj). |
|
Для табл. 8 определены множества S={s1,s2,s3,s4}, X={x1,x2}, Y={y1,y2,y3}. Для частичных автоматов Мили и Мура в рассмотренных таблицах на месте неопределенных состояний и выходных сигналов ставится прочерк.
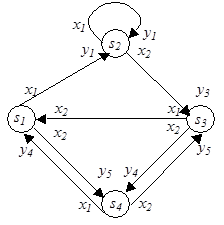
Граф автомата – это ориентированный граф, вершины которого соответствуют состояниям, а дуги – переходам между ними. Дуга, направленная из вершины sj в вершину ss, задает переход в автомате из состояния sj в состояние ss. В начале дуги записывается входной сигнал xi, вызывающий данный переход, т. е. ss = d(sj, xi). Для графа автомата Мили выходной сигнал yg, формируемый на переходе, записывается в конце дуги, а для автомата Мура – рядом с вершиной sj, отмечающей состояние sj, в котором он формируется. Графы автоматов Мили и Мура, построенные по табл. 7 и табл. 8, приведены на рис. 14 и рис. 15 соответственно.
| 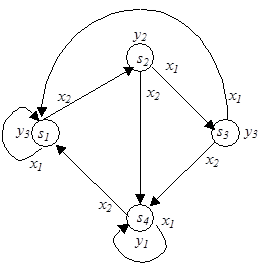
|
| Рис. 14 | Рис. 15 |
С помощью графа автомата легко выделить следующие характерные типы его состояний:
1) преходящее состояние, из которого можно перейти, по крайней мере, в одно другое состояние, но после этого уже нельзя возвратиться в него ни при каком воздействии (соответствующая вершина не имеет заходящих дуг, но имеет хотя бы одну исходящею дугу);
2) тупиковое состояние, в которое можно перейти, по крайней мере, из одного другого состояния, но после этого уже нельзя выйти из него ни при каком воздействии (соответствующая вершина не имеет исходящих дуг в другие вершины, но имеет хотя бы одну входящую дугу из другой вершины);
3) изолированное состояние, из которого нельзя перейти ни в какое другое состояние и в него нельзя попасть ни из какого другого состояния (соответствующая вершина содержит только петлю).
Реализация конечных автоматов сводится к синтезу соответствующей комбинационной схемы, преобразующей входные переменные 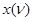 и
и 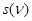 в выходные переменные
в выходные переменные 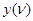 и
и 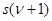 в соответствии с заданными характеристическими функциями
в соответствии с заданными характеристическими функциями 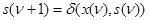 и
и 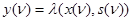 . Для сохранения состояний
. Для сохранения состояний 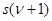 до следующего такта в цепь обратной связи вводится необходимое количество элементов памяти. При реализации автоматов в двоичном алфавите можно использовать рассмотренные ранее методы синтеза комбинационных схем. Но для этого необходимо закодировать состояния схемы и представить характеристические функции в виде булевых функций двоичных переменных. Такое кодирование можно осуществить преобразованием общей (совмещенной) таблицы перехода автомата к таблице соответствия в двоичном структурном алфавите. Если элементы множеств X, Y и S пронумерованы порядковыми числами, начиная с нуля, то им соответствуют коды, представляющие собой двоичные эквиваленты этих чисел. Пусть, например, автомат задан таблицей переходов (табл. 9) и таблицей выходов (табл. 10). Пронумеровав элементы множеств X, Y и S порядковыми числами, например, X={0,1,2,3}, Y ={0,1} и S ={0,1,2,3}, можно получить таблицу переходов (табл. 11), таблицу выходов (табл. 12) и общую (совмещенную) таблицу (табл.13). Далее эту таблицу можно преобразовать к виду (табл. 14).
до следующего такта в цепь обратной связи вводится необходимое количество элементов памяти. При реализации автоматов в двоичном алфавите можно использовать рассмотренные ранее методы синтеза комбинационных схем. Но для этого необходимо закодировать состояния схемы и представить характеристические функции в виде булевых функций двоичных переменных. Такое кодирование можно осуществить преобразованием общей (совмещенной) таблицы перехода автомата к таблице соответствия в двоичном структурном алфавите. Если элементы множеств X, Y и S пронумерованы порядковыми числами, начиная с нуля, то им соответствуют коды, представляющие собой двоичные эквиваленты этих чисел. Пусть, например, автомат задан таблицей переходов (табл. 9) и таблицей выходов (табл. 10). Пронумеровав элементы множеств X, Y и S порядковыми числами, например, X={0,1,2,3}, Y ={0,1} и S ={0,1,2,3}, можно получить таблицу переходов (табл. 11), таблицу выходов (табл. 12) и общую (совмещенную) таблицу (табл.13). Далее эту таблицу можно преобразовать к виду (табл. 14).
| Табл. 9 | Табл. 10 | |||||||||
| x1 | x2 | x3 | x4 | x1 | x2 | x3 | x4 | |||
| s1 | s4 | s3 | s2 | s4 | s1 | y1 | y1 | y1 | y1 | |
| s2 | s4 | s3 | s2 | s4 | s2 | y2 | y1 | y1 | y2 | |
| s3 | s4 | s3 | s3 | s4 | s3 | y2 | y1 | y2 | y2 | |
| s4 | s4 | s1 | s1 | s2 | s4 | y1 | y1 | y2 | y2 |
| Табл. 11 | Табл. 12 | Табл. 13 | ||||||||||||||
| xi si | xi si | xi si | ||||||||||||||
| 3/0 | 2/0 | 1/0 | 3/0 | |||||||||||||
| 3/1 | 2/0 | 1/0 | 3/1 | |||||||||||||
| 3/1 | 2/0 | 2/1 | 3/1 | |||||||||||||
| 3/0 | 0/0 | 0/1 | 1/1 |
| Табл. 14 | |||||||||||||||||||
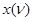
| |||||||||||||||||||
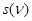
| |||||||||||||||||||
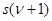
| |||||||||||||||||||
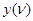
|
Заменяя десятичные числа в табл. 14 их двоичными эквивалентами, читаемыми сверху вниз, получаем таблицу соответствия (табл. 15), в которой значения функций 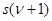 и
и 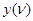 представлены двоичными кодами.
представлены двоичными кодами.
Из табл. 15 видно, что комбинационная схема должна иметь четыре входа, соответствующие входным переменным 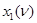 ,
, 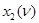 и переменным состояния
и переменным состояния 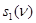 ,
, 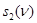 , а также три выхода, соответствующие переменным состояния
, а также три выхода, соответствующие переменным состояния 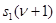 ,
, 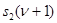 и выходной переменной
и выходной переменной 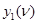 . Синтезировав комбинационную схему, соответствующую полученной таблице истинности (табл. 15) и введя два элемента памяти (триггера) T1 и T2, построим структурную схему автомата (рис. 16).
. Синтезировав комбинационную схему, соответствующую полученной таблице истинности (табл. 15) и введя два элемента памяти (триггера) T1 и T2, построим структурную схему автомата (рис. 16).
| Табл. 15 | ||||||||||||||||||||
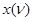
| 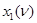
| |||||||||||||||||||
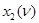
| ||||||||||||||||||||
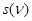
| 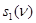
| |||||||||||||||||||
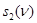
| ||||||||||||||||||||
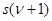
| 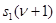
| |||||||||||||||||||
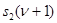
| ||||||||||||||||||||
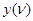
| 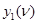
|
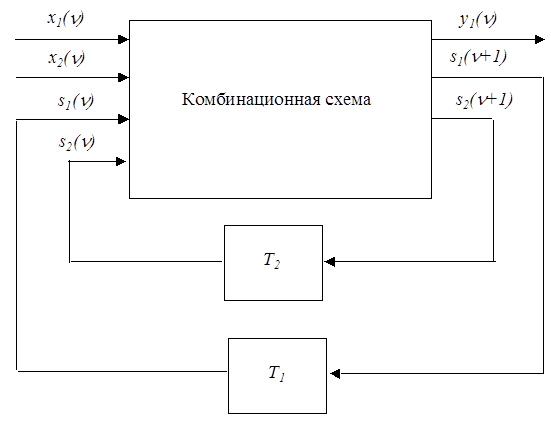
|
| Рис. 16. |
Контрольные вопросы к лекции 5
5-1. Чем последовательностные устройства отличаются от комбинационных?
5-2. Какой автомат называется конечным?
5-3. Что содержит множество состояний автомата?
5-4. Почему последовательностные схемы называются автоматами с памятью?
5-5. Как описывается конечный автомат?
5-6. Какие функции называются характеристическими функциями конечного автомата?
5-7. Что связывает функция переходов конечного автомата?
5-8. Что связывает функция выходов конечного автомата?
5-9. Из каких структурных элементов состоит общая блок-схема конечного автомата?
5-10. Чем отличаются автоматы первого и второго рода?
5-11. Какой автомат называется инициальным?
5-12. Какой автомат называется полностью определенным?
5-13. Какой автомат называется частичным?
5-14. Что представляет собой граф автомата?
5-15. Чему соответствуют вершины графа автомата?
5-16. Чему соответствуют дуги графа автомата?
5-17. Как размечаются дуги графа автомата первого рода?
5-18. Как размечаются дуги графа автомата второго рода?
5-19. Какое состояние автомата называется преходящим?
5-20. Какое состояние автомата называется тупиковым?
5-21. Какое состояние автомата называется изолированным?
5-22. Чем определяется количество элементов памяти в структурной схеме автомата?
5-23. На основе чего синтезируется комбинационная схема в структурной схеме автомата?
Дата добавления: 2016-09-06; просмотров: 3889;











