Влияние начальных несовершенств

До сих пор мы рассматривали задачу устойчивости стержня в идеализированной постановке. Считалось, что стержень идеально прямой, продольная нагрузка приложена строго по оси, а поперечная отсутствует. В реальных конструкциях этого, естественно, не бывает. Выясним насколько существенно влияют на поведение сжатого стержня те или иные отклонения от принятых допущений.

Как было показано в Лекции 2 на примере систем с одной степенью свободы, точки бифуркации свойственны только идеальным системам. Для систем с несовершенствами точки бифуркации первого рода исчезают - система не теряет устойчивости, а плавно отклоняется, причем отклонение резко увеличивается при приближении нагрузки к значению, критическому для идеальной системы.

Для стержневых систем характерно именно такое поведение, а не перескок в новое положение равновесия, свойственный точкам бифуркации второго рода и предельным точкам.

Покажем это на примере стержня, шарнирно опертого по концам.

А. Стержень с начальной погибью

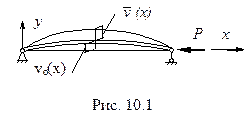
Дифференциальное уравнение равновесия такого стержня в отклоненном положении можно составить, приравняв момент внутренних упругих сил к внешнему моменту

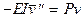. (10.1)

В левую часть равенства входит только “упругий” прогиб, т.е. отклонение от первоначального искривленного, но ненагруженного состояния. В правую - полный прогиб

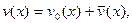(10.2)

где 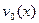- “начальная погибь” стержня в плоскости изгиба.

Подставив (10.2) в (10.1), получаем уравнение

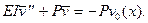(10.3)

Присоединив к (10.3) граничные условия

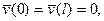
приходим к краевой задаче для неоднородного уравнения.

Решение такой задачи обычно строят в виде разложения по собственным функциям однородной задачи. В данном случае

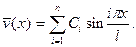(10.4)

Подставив (10.4) в (10.3), имеем

. (10.5)

Разложив 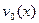в аналогичный ряд

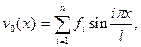(10.6)

где

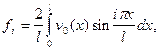(10.7)

мы, вследствие ортогональности системы собственных функций, получаем

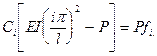(10.8)

Поскольку собственные значения аналогичной задачи для идеально прямого стержня известны

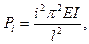(10.9)

соотношение (10.8) можно переписать в виде

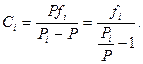(10.10)

Таким образом отклоненная форма равновесия (10.4)

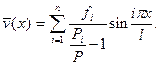(10.11)

Суммарный прогиб согласно (10.2),(10.6), (10.11)

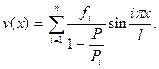(10.12)

Легко видеть, что при стремлении 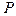к любой из 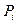, амплитуда i-той гармоники стремится к бесконечности. Это означает, что нагрузка 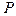не может достичь даже первой из 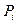, т.е. 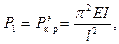ибо при любых сколь угодно малых 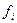амплитуда первой гармоники при становится доминирующей. Это обстоятельство позволяет принять приближенное решение в форме

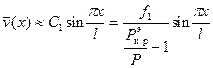(10.13)

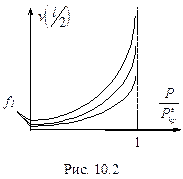
На рис.10.2 показана зависимость макси-мального прогиба 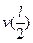от 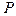при различных .

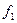Таким образом, стержень с начальной погибью не теряет устойчивости в традиционном смысле. О критической нагрузке для него можно говорить лишь в том смысле, что такая нагрузка, равная 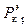, является недопустимой. Но уже значительно раньше недопустимо большими могут стать прогибы, а вместе с ними и нормальные напряжения

.

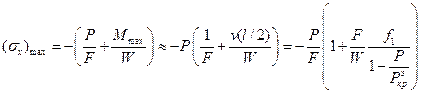Так для сплошного прямоугольного сечения высотой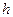

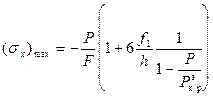
Даже при незначительной погиби 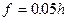эти напряжения вдвое превышают напряжения сжатия уже при .

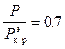Аналогично решается задача и при других вариантах опирания концов стержня. В общем случае надо исходить вместо (10.3) из уравнения четвертого порядка

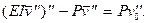
Отыскивая его решение в форме

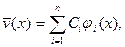
где 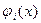- собственные функции однородной задачи (т.е. собственные формы идеально прямого стержня), мы снова придем к формуле

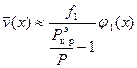, (10.14)

где 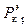- критическая сила прямого стержня, а

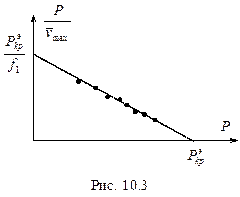
До сих пор мы предполагали, что начальная погибь 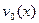известна. Как правило, измерить ее очень не просто.

Однако ее можно определить экспериментально с помощью метода Саусвелла, основанного на структуре формул (10.13), (10.14). Для шарнирно опертого стержня

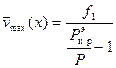. (10.15)

Перепишем (10.15) в виде

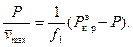(10.16 )

Построив экспериментально путем нескольких замеров график (рис.9.3) и понимая, что он согласно (10.16) обязан быть линейным, можно экстраполировать полученную зависимость вправо и влево, и графически найт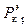и и .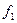

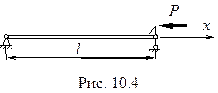
Б. Эксцентрично сжатый стержень

Пусть к идеально прямому шарнирно опертому стержню нагрузка приложена параллельно оси с эксцентриситетом .

Дифференциальное уравнение, аналогичное (10.3),

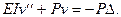(10.17)

Очевидно, что решение может быть получено из решения предыдущей задачи при 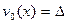. Разложив 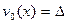в ряд (10.6), будем иметь

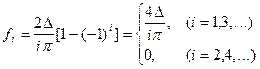(10.18)

Таким образом, результат будет тем же, что и в предыдущем случае при

.

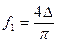В. Продольно-поперечный изгиб

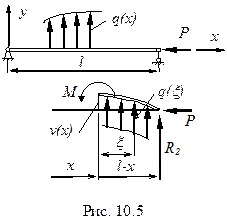
Пусть кроме приложенной строго по оси силы 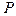на идеально прямой стержень действует некоторая поперечная нагрузка .

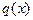Эта нагрузка порождает в опорах реакции 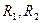и совместно с продольной силой 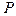вызывает в произвольном сечении балки изгибающий момент

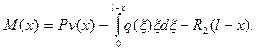(10.19)

В результате дифференциальное уравнение равновесия для этого случая

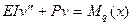, (10.20)

где

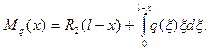(10.21)

Легко видеть, что мы снова получили уравнение вида (10.3) при

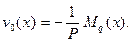(10.22)

Разложив эту функцию в ряд (10.6), получим

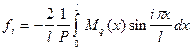. (10.23)

Теперь мы можем воспользоваться результатом, полученным для случая А

.

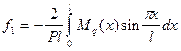В частности, для массивного стержня, где весом нельзя пренебречь, имеем

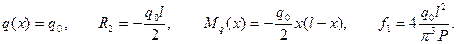
Рассмотренные случаи позволяют сделать общий вывод. Стержни с начальными несовершенствами устойчивости в классическом смысле не теряют. С ростом нагрузки их прогибы плавно увеличиваются и при 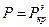обращаются в бесконечность. Поскольку такая нагрузка недопустима, ее иногда называют критической. Реально допустимая нагрузка 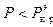. Она определяется по предельно допустимым прогибам или напряжениям 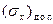при изгибе стержня.