Устойчивость при комбинированном нагружении

Как правило, системы испытывают не одно, а несколько независимых силовых воздействий. Устойчивость таких систем зависит от комбинации параметров воздействий.

Пример 3.1

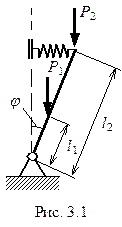
Та же система, что в Примере 1.2, нагружена двумя силами. Если действует одна из этих сил, то при отсутствии другой

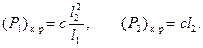(3.6)

Если действуют одновременно обе силы, то линеаризованное уравнение равновесия

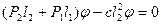
дает условие существования нетривиального решения

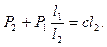(3.7)

Геометрически это условие представляет собой прямую (Рис.3.2), ограничивающую область устойчивости, то есть область таких комбинаци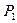й и 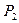, при которых вертикальное положение равновесия остается устойчивым. С учетом (3.6) условие (3.7) может быть переписано в виде

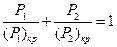
Если на систему с одной степенью свободы действуют не две, а 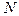сил, то уравнение границы области устойчивости в 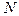- мерном пространстве имеет вид

,

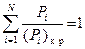а устойчивость проверяется неравенством

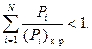
В теории устойчивости доказывается теорема, что при наших предположениях о докритических напряжениях, определяемых линейной теорией упругости, и отсутствии докритических перемещений, граница области устойчивости может быть криволинейной, разомкнутой, замкнутой, но всегда выпуклой.