МАРШЕВЫЙ МЕТОД РАСЧЕТА СВЕРХЗВУКОВЫХ ТЕЧЕНИЙ

Система уравнений, описывающая стационарное течение невязкого нетеплопроводного газа в цилиндрической системе координат, в форме законов сохранения в матричной записи имеет вид

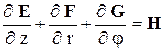, (3.1)

где .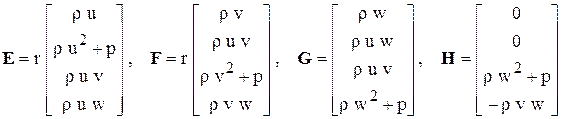

Здесь p - давление, r - плотность, (u, v, w) – составляющие вектора скорости соответственно в направлениях (z, r, j) (рис.3.1).

Система (3.1) представляет собой законы сохранения массы, импульса в проекциях на оси координат. Уравнение энергии в стационарном случае представляет собой интеграл Бернулли, и для совершенного газа с показателем адиабаты g имеет вид

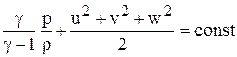(3.2)

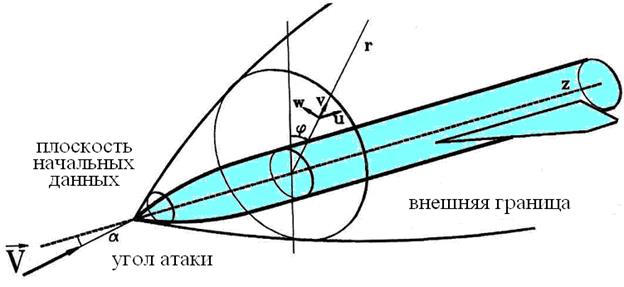
Рис.3.1

Геометрия тела и внешней ударной волны описывается следующими зависимостями: r_т = r_т(z), r_в = r_в(z,j), где r_т(z) - известная функция, описывающая профиль осесимметричного тела, r_в - радиус ударной волны, который должен определяться в процессе решения задачи. Предполагается, что можно оценить радиус ударной волны: r_в(z,j) < r_м(z), где r_м(z) - известная функция. Следовательно, на поверхности r = r_м(z) условия в набегающем потоке.

На поверхности тела выполнено условие непротекания: 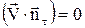, где 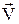- вектор скорости, 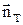- единичная нормаль к поверхности тела.

Предполагается, что при z = z_o начальные данные заданы, причем местные числа Маха в направлении z во всей области больше единицы. Таким образом, рассматривается гиперболическая система квазилинейных уравнений с пятью неизвестными функциями от трех независимых переменных. Область, в которой ищется решение при z > z_o, ограничена поверхностью тела, внешней границей в невозмущенном потоке.

Перейдем к новым независимым переменным по формулам:

z = z, 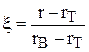, j = j (3.3)

Это преобразование обеспечивает нормировку расчетной области в радиальном направлении. Преобразованная система (3.1) в новых переменных, записанная в дивергентной форме, имеет вид

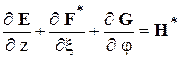, (3.4)

где F^* = f₁E+f₂F, H^* = H-gE, 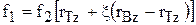, , 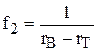, 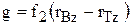нижний индекс «z» означает производную функции по z.

Уравнения (3.4) могут быть проинтегрированы по переменной z, в результате определяются компоненты консервативной переменной E, по которым могут быть найдены физические компоненты p, r, u, v, w. Процедура нахождения этих переменных заключается в решении нелинейных алгебраических уравнений: уравнение (3.2) и уравнений для E_i, i = 1,2,3,4 с пятью газодинамическими параметрами. Имеем

, , , , .

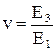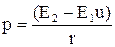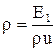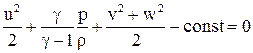Последнее уравнение может быть разрешено относительно скорости u, и с учетом того, что течение должно быть сверхзвуковым, имеем

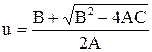, где , , .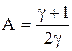

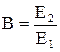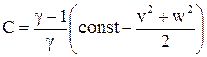Для интегрирования системы уравнений (3.4) применяется метод [17]. Разностные формулы аналогичны выражениям, приведенным в гл. 2. Рассмотрим схему удовлетворения граничным условиям.

На поверхности тела должно быть выполнено условие непротекания. В случае цилиндрической системы координат для вектора скорости и нормали к поверхности осесимметричного тела имеем следующие выражения:

, .

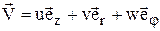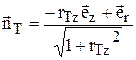Путем применения схемы «предиктор - корректор», в результате чего находятся значения консервативных переменных на новом слое по z, затеем происходит переход к физическим переменным и определение, в частности, значения p_w¢, r_w¢, u_w¢, v_w¢, w_w¢ (индекс «w» обозначает значения на поверхности тела; индекс «¢» - то, что это предварительные значения). Вектор скорости 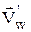= (u_w¢, v_w¢, w_w¢) не удовлетворяет условию непротекания и должен быть повернут от касательной плоскости тела на некоторый угол d, определяемый выражением 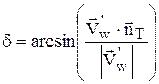(3.5)

Если d > 0, то при повороте вектора скорости происходит расширение потока, если d < 0 - сжатие. Алгоритм удовлетворения граничным условиям подобен алгоритму, описанному в гл.2, с обеспечением постоянства энтропии на поверхности тела. После определения угла поворота вектора скорости в соответствии с (3.5) находится давление p_w по формуле

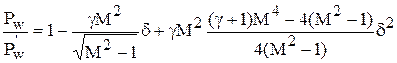
Далее вычисляется плотность 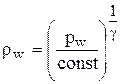, где сonst определяется согласно давлению и плотности в критической точке на наветренной стороне корпуса и постоянна для всей поверхности тела.

Величину вектора скорости находят из интеграла Бернулли:

.

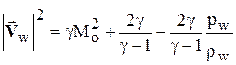Так как вектор 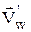был повернут в плоскости векторов 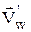, 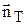на угол d, то направление скорости 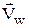теперь должно совпадать с направлением: 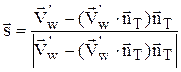, то есть 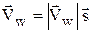. Записывая последнее соотношение в проекциях на оси координат, имеем:

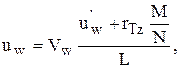
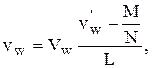
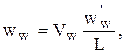
где , ,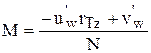

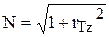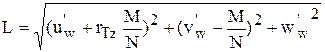
Если рассматривается обтекание без угла скольжения, то в плоскости симметрии течения ставятся соответствующие условия симметрии течения, если с углом скольжения, то соответственно используется условие периодичности. Для удовлетворения данных условий вводится 4 дополнительных луча.

Выбор внешней границы в области невозмущенного потока предполагает использование разностной схемы «сквозного» счета. Наличие внутренних ударных волн требует применения сглаживания. Сглаживание производится аналогично, как и при расчете конических течений.

Для проведения численных расчетов шаг интегрирования по координате z выбирается из условия устойчивости. Ограничения, которые необходимо накладывать на величину шага интегрирования,

, ,

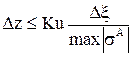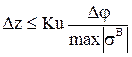где , ,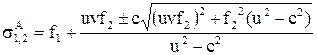

, .

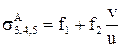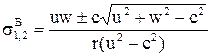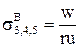Здесь 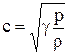- скорость звука, Ku - число Куранта. Обычно в расчетах полагается Ku = 0.7¸0.9. Следует отметить, что все собственные значения, выписанные выше, действительные, так как рассматривается сверхзвуковое течение в направлении z ( u > c ).

Таким образом, описание численного метода решения уравнений Эйлера (3.1) с соответствующими граничными условиями около осесимметричного тела закончено. Главная особенность описанного метода состоит в отказе от выделения головной волны, что, учитывая осесимметричность корпуса, позволяет построить осесимметричную сетку (несмотря на наличие угла атаки) и упростить уравнения.

Распространение метода на расчет осесимметричных тел с оперением (ракет) делается следующим способом. Предположим, оперение расположено в горизонтальной плоскости ( схема «+» ), а оперение в вертикальной плоскости не отклонено и его можно не учитывать. Введем две зоны (или области) расчета: одна расположена выше плоскости, в которой расположено оперение, а другая ниже (рис.3.2). Плоскость, в которой расположено оперение, является границей между двумя зонами. Построив схему удовлетворения граничным условиям на данной границе с учетом оперения, мы тем самым без каких-либо затруднений будем иметь расчетную сетку, которая позволит выделить оперение достаточно удовлетворительным способом, связывая расчетную сетку только с поверхностью корпуса ракеты.

Данный упрощенный многозонный подход применим в случае, когда консоли исследуемой ракетной компоновки, имеющие малую относительную толщину и острые передние кромки, слабо отклонены от азимутальных координатных плоскостей. При выполнении этих условий применимо приближение тонкого крыла, согласно которому граничное условие непротекания, включающее в себя только направляющие косинусы поверхности крыла, но не координаты этой поверхности, задается не на истинной поверхности крыла, а на близкой к ней азимутальной координатной плоскости.

На границе между двумя зонами расчетные узлы могут быть либо обычными внутренними узлами, и тогда должны быть поставлены условия сопряжения (непрерывности) течения между зонами, Либо узлами, принадлежащими поверхности оперения. В последнем случае граничным условием служит условие непротекания, и течение на наветренной и подветренной сторонах рассчитывается отдельно. Для удовлетворения данным граничным условиям на общей границе двух зон для каждой зоны вводится два дополнительных луча (так же как для удовлетворения условию симметрии потока).

Рис.3.2

Схема удовлетворения граничным условиям выполняется после выполнения шага «корректор» для обеих зон и строится следующим образом:

1) если граничный узел внутренний, то условие непрерывности реализуется путем замены значений газодинамических функций на двух крайних лучах зоны значениями данных функций на этих же лучах в физическом пространстве, но из другой зоны, которые являются внутренними для нее. Пусть [n-2] - номер луча, соответствующий границе между зонами для обеих зон, тогда лучи [n-1], [n] (дополнительные лучи) из первой зоны (условно) соответствуют [n-3], [n-4] - лучам из второй зоны, а [n-1], [n] - лучи из второй зоны зоны соответствуют [n-3], [n-4] - лучам из первой зоны. Тогда условие непрерывности течения реализуется по формулам

U¹_n-1,j = U²_n-3,j , U¹_n,j = U²_n-2,j , U²_n-1,j = U¹_n-3,j , U²_n,j = U¹_n-2,j .

Здесь U¹_i,j, U²_i,j - газодинамические функции соответственно в первой и во второй областях в узле [i, j] (i- номер луча, j- номер узла по радиусу). Фактически данный способ просто позволяет сделать шаг в каждой зоне независимо друг от друга, а после выполнения шага интегрирования производится обмен информацией, которая берется во внутренних узлах.

2) если граничный узел принадлежит поверхности крыла, ограничимся случаем, когда крыло не изогнуто, т.е. проекция от нормали к поверхности крыла на ось r равна 0. Тогда уравнение нормали к поверхности крыла с симметричным профилем (профиль характеризуется углом наклона к срединной линии - j, рис.3.3) и отклоненной на угол d можно записать в виде:

- на подветренной стороне ;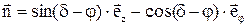

- на наветренной стороне .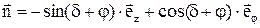

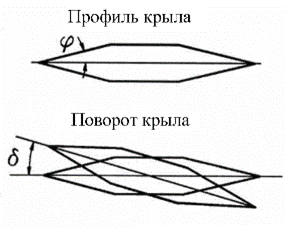
Рис.3.3

После определения нормали к поверхности крыла удовлетворение граничным условиям происходит в соответствии с алгоритмом удовлетворения граничному условию непротекания на поверхности корпуса. При этом используются и корректируются значения газодинамических функций на [n-2] -луче (в терминах, приведенных выше) - U¹_n-2,j и U²_n-2,j. Затем корректируется значения газодинамических функций и на лучах [n] и [n-1] для обеих зон (k = 1,2) по формулам U^k_n,j = U^k_n-2,j , U^k_n,j = U^k_{n-1,j .}

Такая замена газодинамических функций на «мнимых» лучах имитирует плоский поток газа, одинаково направленный с потоком на соответствующей поверхности крыла.

Следуя [9] для учета эффектов вращения, можно использовать гипотезу искривления. Вращение оперения вокруг оси тела (вращение осесимметричного корпуса в рамках уравнений Эйлера не оказывает влияния на течение) приводит к тому, что в произвольной точке консоли появляется дополнительный местный угол атаки 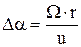, где W - угловая скорость, r - радиус точки на поверхности консоли, u - компонента скорости газа вдоль оси тела. Уравнение нормали к поверхности крыла в этом случае имеет вид:

- на подветренной стороне ;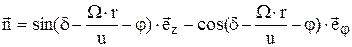

- на наветренной стороне .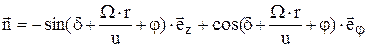

Таким образом, задача о нестационарном течении около вращающегося оперенного тела может быть сведена к стационарной задаче с искривленными консолями оперения.

Отказ от выделения головной волны и построение осесимметричной сетки позволили построить простой алгоритм удовлетворения граничным условиям непротекания на поверхности оперения.