Прием груза на судно
Пусть груз весом Р необходимо принять в точку А с координатами хг, уг, zг. В исходном состоянии судно считается сидящим прямо (θ = 0) и на ровный киль (ψ = 0).
Процесс приема груза удобно рассматривать поэтапно: вначале, условно, груз размещаем на уровне центра тяжести судна, затем перемещаем его на уровень горизонтальной плоскости, в которой он будет оставаться при последующих перемещениях в конечную точку А.
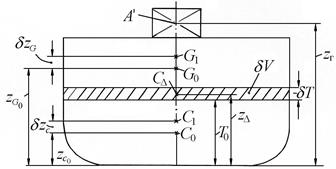
Прием груза на конечный уровень по высоте. На первом этапе груз принимается в точку G0 c координатами 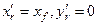 и
и 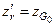 (рис. 2.12), где хf – абсцисса центра тяжести площади начальной ватерлинии.
(рис. 2.12), где хf – абсцисса центра тяжести площади начальной ватерлинии.
Очевидно, что при исходной посадке прямо и на ровный киль, размещение центра тяжести груза в вертикальных плоскостях, проходящих через оси наклонения судна, не вызовет его наклонения.
После приема груза вес судна будет равен 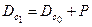 , а средняя осадка
, а средняя осадка 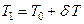 , где
, где
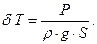
| (2.13) |
|
Рис. 2.12. Прием груза без наклонения судна
В (2.13) обозначено:
| S | – | площадь действующей ватерлинии, м2; |
| ρ | – | плотность воды, т/м3; |
| g | – | 9,81 м/с2 – ускорение свободного падения. |
На втором этапе центр тяжести груза перемещаем их точки Go в точку  (рис. 2.12). Изменение положения центра тяжести судна
(рис. 2.12). Изменение положения центра тяжести судна  после перемещения груза с уровня
после перемещения груза с уровня 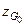 на конечный уровень по высоте, т.е. на уровень
на конечный уровень по высоте, т.е. на уровень 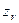 (точка
(точка 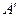 ) можно определить на основании теоремы о перемещении центра тяжести системы:
) можно определить на основании теоремы о перемещении центра тяжести системы:
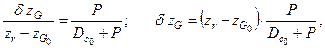
| (2.14) |
| где | 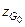
| – | аппликата начального положения центра тяжести судна. |
Прием груза в общем случае вызовет изменение положения центра тяжести судна, центра величины и метацентров.
Если до приема груза поперечная метацентрическая высота составляла 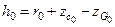 , то после приема ее значение будет определяться как
, то после приема ее значение будет определяться как 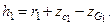
Изменение поперечной метацентрической высоты
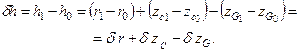
| (2.15) |
Как видно, изменение метацентрической высоты включает три составляющие, которые и нужно вычислить.
Изменение метацентрического радиуса можно найти, исходя из формулы для его определения
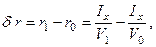
| где | Ix | – | момент инерции площади действующей ватерлинии, который можно считать неизменным в силу того, что при приеме малого груза ватерлиния не изменяется; |
| V1 | – | объемное водоизмещение судна после приема груза; превышает начальное водоизмещения (V0) на величину объема δV, вошедшего в воду (см. рис. 12). |
Преобразуя последнее выражение и перехода от объемов к весам, можно получить
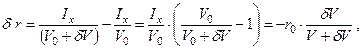
или
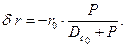
| (2.16) |
Изменение положения центра величины судна, вследствие приема груза и появления по этой причине слоя водоизмещения δV, можно определить аналогично тому, как это показано выше для центра тяжести судна (δzG). Условно будем считать, что в начальный момент центр добавочного слоя водоизмещения совпадает с центром величины судна без груза (точка С0). Затем центр объема перемещаем из точки С0 в точку СΔ с аппликатой 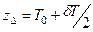 , которая является действительным центром объема δV.
, которая является действительным центром объема δV.
В соответствии с отмеченным по теореме о перемещении центра тяжести системы, можно получить
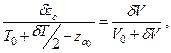
откуда 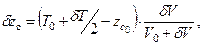
или 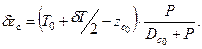
| (2.17) |
Подставив выражения (2.14), (2.16), (2.17) в (2.15), найдем изменение метацентрической высоты
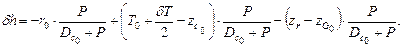
Раскрывая скобки, получим
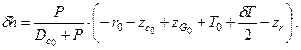
Первые три члена в скобках дают значение начальной метацентрической высоты до приема груза (h0). Учитывая это, можно получить окончательное выражение для изменения поперечной метацентрической высоты
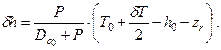
| (2.18) |
В итоге, метацентрическая высота после приема груза определяется по формуле
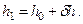
| (2.19) |
Изменение остойчивости удобно оценивать с использованием коэффициентов остойчивости.
Коэффициент поперечной остойчивости судна с грузом можно получить с использованием формул (18) и (19)
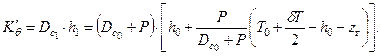
|
После раскрытия скобок и сокращений получаем
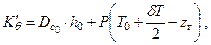
или
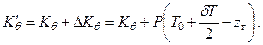
| (2.20) |
Для определения продольной метацентрической высоты и продольного коэффициента остойчивости судна с принятым грузом изложенные выше рассуждения могут быть повторены и получены следующие формулы:
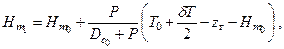
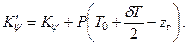
| (2.21) |
Из выражений (2.20) и (2.21) можно выявить условие приема груза без изменения остойчивости судна. Для этого положим равным нулю сомножитель в скобках, т.е. 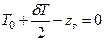 , откуда
, откуда
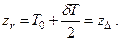
Остойчивость судна не изменяется, если центр тяжести груза (рис. 2.13) располагается на одном уровне с центром тяжести добавочного слоя водоизмещения, т.е. zг = z∆. Этот уровень принято называть «нейтральной плоскостью» при принятии груза.
Если груз принимается ниже центра добавочного слоя водоизмещения, то zг < z∆ и остойчивость судна увеличивается; при zг > z∆ остойчивость уменьшается. В этом нетрудно убедиться, рассмотрев рис. 2.13.
|
Рис. 2.13. К изменению остойчивости при приеме груза
На судно принят груз весом P, у которого цент тяжести располагается в точке А. Вследствие приема груза увеличиваются осадка на δT и объемное водоизмещение – на δV. Сообщим судну (условно) равнообъемное наклонение на угол θ. В этом случае вектора Р и (ρ∙g∙δV) будут направлены перпендикулярно к ватерлинии 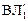 ; они образуют момент, влияющий на остойчивость. Этот момент (∆М = Рl∆) изменяется как по величине, так и по направлению его действия при изменении взаимного положения векторов [Р и (ρ∙g∙δV)] или, иначе, точек
; они образуют момент, влияющий на остойчивость. Этот момент (∆М = Рl∆) изменяется как по величине, так и по направлению его действия при изменении взаимного положения векторов [Р и (ρ∙g∙δV)] или, иначе, точек 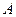 и С∆.
и С∆.
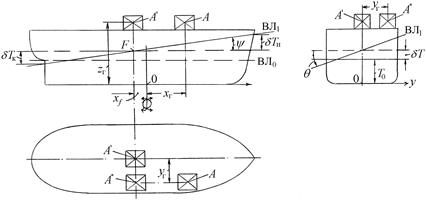
Горизонтальное перемещение груза в конечное положение. Задача об определении посадки судна после приема груза в точку А с координатами хг, уг, zг (конечное положение) решается после нахождения значений веса и средней осадки судна с грузом, а также соответствующих коэффициентов продольной и поперечной остойчивости.
Угол крена судна вычисляется как результат поперечного перемещения груза из точки 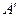 с координатами хf, у = 0, zг в точку
с координатами хf, у = 0, zг в точку 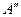 с координатами xf, yг, zг (рис. 2.14). Плечо поперечного перемещения будет равно ординате центра тяжести груза (уг).
с координатами xf, yг, zг (рис. 2.14). Плечо поперечного перемещения будет равно ординате центра тяжести груза (уг).
Угол крена определяется по выражению
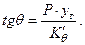
Осадка правого и левого бортов после наклонения с учетом (2.13) определяется по формулам:
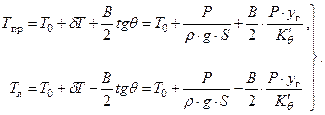
| (2.22) |
При расчете по формулам (2.22) значение ординаты груза (уг) вносится с соответствующим знаком (плюс или минус).
В результате продольного перемещения груза из точки 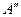 в точку А (рис. 2.14) на расстояние (хг – хf) образуется дифферент судна; тангенс угла дифферента определяется по формуле
в точку А (рис. 2.14) на расстояние (хг – хf) образуется дифферент судна; тангенс угла дифферента определяется по формуле
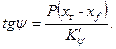
| (2.23) |
|
Рис. 2.14. К определению посадки при приеме груза
Изменение осадки носом и кормой вследствие появления дифферента:
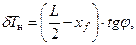 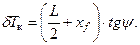
|
Осадки носом и кормой
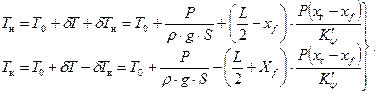
| (2.24) |
При применении формул (2.23), (2.24) значение абсцисс хг и хf вносится с соответствующим знаком (плюс или минус).
Дата добавления: 2018-11-26; просмотров: 991;











