Зависимости для расчета момента инерции

<1 2 345 6 7 >

Вид фигуры	Момент инерции площади фигуры относительно «у–у», «а–а»

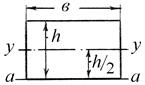
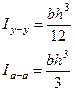
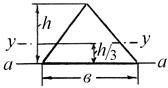
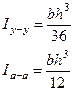
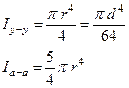
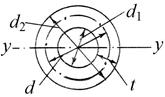
Для прямоугольного понтона с размерами погруженного объема: L, B и T поперечный и продольный метацентрические радиусы находят по следующим выражениям

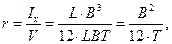
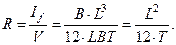
Поперечный метацентрический радиус судна может быть определен по приближенным формулам, наиболее употребительной из которых являются

r ≃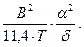

где	a	–	коэффициент полноты площади ватерлинии;
	d	–	коэффициент полноты водоизмещения.

Приближенная формула для продольного метацентрического радиуса

r≃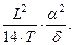

Сравнивая значения поперечного и продольного радиусов, нетрудно увидеть, что продольный метацентрический радиус примерно в (L/B)² раз превышает поперечный; в связи с этим радиусы принято называть: «большой» и «малый».

Зависимости начальных метацентрических радиусов и центральных моментов инерции площади ватерлинии от погружения судна входят в группу кривых элементов начальной остойчивости; они строятся на одном графике с кривыми плавучести.

Метацентрические формулы остойчивости.

<1 2 345 6 7 >

Дата добавления: 2018-11-26; просмотров: 506;