Струйная гидравлическая модель потока
Задание поля скорости и поля вихрей теоретически позволяет определить мгновенные значения скорости и угловой скорости 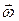 в каждой точке пространства, занятого жидкостью. К числу таких параметров, отражающих кинематику движения конечных масс жидкости, относятся, в первую очередь, расход жидкости, средняя скорость течения жидкости и интенсивность вихревого движения.
в каждой точке пространства, занятого жидкостью. К числу таких параметров, отражающих кинематику движения конечных масс жидкости, относятся, в первую очередь, расход жидкости, средняя скорость течения жидкости и интенсивность вихревого движения.
Струйная модель потока жидкости. В соответствии с этой моделью весь поток жидкости представляется как совокупность отдельных элементарных струек жидкости, не перемешивающихся между собой, с бесконечно малым поперечным сечением, в пределах которого локальную скорость жидкости можно считать постоянной. Струйная модель потока жидкости введена Эйлером. Основу этой модели составляет понятие струйке, под которой понимают жидкость, протекающую внутри трубки тока, сформированной из линий тока.
Линия тока
В движущейся жидкости условно выберем линию таким образом, чтобы в каждой точке ее скорость была направлена по касательной. Линией тока называется кривая, обладающая тем свойством, что в данный момент времени векторы скоростей в любой ее точке совпадают по направлению с касательными ( рис. 4.4)
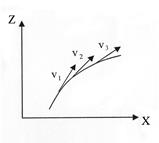
Рис. 4.4 Определение линии тока
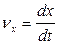 ;
; 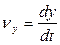 ;
; 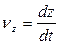 .
.
При одном и том же промежутке времени дифференциальное уравнение линии тока запишется:
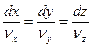 (4.8)
(4.8)
Линии тока не могут пересекаться в одной точке. В противном случае это бы означало, что частица, проходящая через данную точку должна иметь одновременно несколько векторов мгновенной локальной скорости, что противоречит физическому смыслу
Под траекторией понимается след, оставленный конкретной, движущейся частицей в пространстве.
Линия тока отличается от траектории, т.к. она связывает различные, лежащие на ней частицы и характеризует направление их движения в данный момент времени, она может совпадать с траекторией только при стационарном режиме.
Свойства линии тока:
- линии тока некогда не пересекаются;
- зависят от характера движения;
- совпадает с траекторией при стационарном режиме.
Дата добавления: 2016-05-26; просмотров: 2671;











