Уравнение неразрывности или сплошности (уравнение расхода)
Уравнение неразрывности – это частный случай уравнения сохранения массы жидкости во времени для изолированной системы 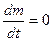 .
.
Условимся считать что жидкость, втекающая в выделенный объем в виде параллелепипеда через первую грань вдоль оси 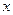 будет положительна, а вытекающая через вторую грань будет отрицательна.
будет положительна, а вытекающая через вторую грань будет отрицательна.
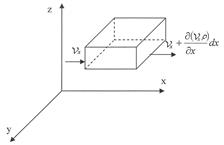
Рис. 4.6 К выводу дифференциального уравнения сплошности
Изменение массы жидкости вытекающей из второй грани вдоль оси 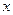 за время
за время 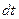 из параллелепипеда составит:
из параллелепипеда составит:
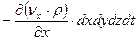 (4.21)
(4.21)
Аналогично на все координатные оси
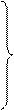
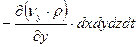 (4.22)
(4.22)
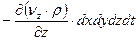
Суммарное изменение массы внутри элементарного параллелепипеда за счет разности приносимой потоком в параллелепипед и уносимой из него массы по трем координатам 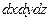 и за время
и за время 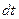 составит
составит
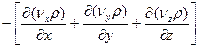 ( 4.23)
( 4.23)
Из математики известно, что:
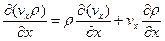
Изменение массы в неизменном объеме возможно только тогда, когда меняется плотность жидкости.
Изменение плотности по координатам с течение времени будет:
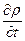
Откуда
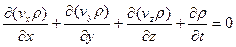 (4.24)
(4.24)
Сгруппировав слагаемые, получим уравнение неразрывности или сплошности:
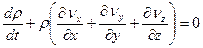 (4.25)
(4.25)
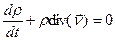
Для несжимаемой жидкости 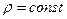 , тогда расход по длине струйки тока не меняется в данный момент времени и имеет одно и тоже значение.
, тогда расход по длине струйки тока не меняется в данный момент времени и имеет одно и тоже значение.
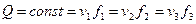 (4.26)
(4.26)
Уравнения (4.26) называются уравнениями неразрывности (расхода) в гидравлической форме для несжимаемой жидкости.
Дата добавления: 2016-05-26; просмотров: 1974;











