Биологическая кинетика

Кинетика и термодинамика биологических процессов

Биологические системы обладают свойствами саморегуляции, то есть способностью перестраиваться в зависимости от внешних воздействий так, чтобы сохранился оптимальный уровень их функционирования.

Существуют различные способы регуляции жизнедеятельности клетки, которые можно условно отнести к генетическому, биохимическому и физиологическому уровням регуляции. В пределах каждого из них действуют механизмы, в основе которых лежит последовательность конкретных метаболических процессов. Понять динамические свойства этих регуляторных механизмов можно лишь на основе общесистемного подхода, рассматривающего поведение каждого из элементов сложной системы как результат его взаимодействия с остальными элементами.

Одним из наиболее развитых подходов для решения этой проблемы в современной биофизике является математическое моделирование. В соответствующих кинетических моделях отражена динамика изменения концентраций различных составных элементов биологической системы, которая определяется скоростями отдельных элементарных реакций.

Биологическая кинетика

В основе процессов обмена клетки со средой и внутреннего метаболизма лежит сложная сеть различных реакций, организованных определенным образом во времени и пространстве. В результате этих процессов изменяются концентрации различных веществ, численность отдельных клеток, биомасса организмов, могут изменяться и другие величины, например величина трансмембранного потенциала в клетке. Изменения всех этих переменных величин во времени и составляют кинетику биологических процессов. Основные исходные предпосылки при описании кинетики в биологических системах, в общем, такие же, как и в химической кинетике.

Рассмотрим простейший пример замкнутой популяции клеток, в которой одновременно происходят процессы размножения и гибели и в избытке имеются питательные вещества. Возникает вопрос, как меняется численность клеток в такой системе со временем и может ли в ней, в конце концов, установиться стационарное состояние, когда число клеток меняться не будет. Это типичная кинетическая задача, которая решается с помощью обычных дифференциальных уравнений. Пусть в некоторый момент времени t концентрация клеток в среде составит N. Скорость dN/ dt изменения концентрации клеток в среде складывается из скорости их размножения V_{разм н} и скорости гибели V_гиб:

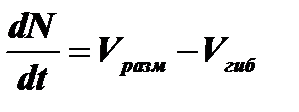
В простом случае скорость размножения, то есть увеличение концентрации клеток в единицу времени, пропорциональна их численности в каждый момент: V_pamH = kjN, где к_} - константа пропорциональности, зависящая от условий среды (температура, наличие питательных веществ и др.).

Аналогично V_m6 =k₂N, где к₂ - константа пропорциональности, определяющая интенсивность процессов гибели клеток. Отсюда следует, что

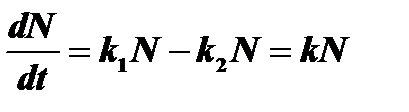
Решив это уравнение, мы найдем, как меняется концентрация клеток в среде N = N(dt): N = N₍₎e^kt где N₀ - концентрация клеток в начальный момент времени t = 0 наблюдения за системой.

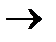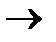Легко видеть, что в зависимости от состояния констант скоростей процес­сов гибели к₂ и размножения судьба этой популяции будет различной. Если к_} > к₂, к > 0, то и в системе будет происходить неограниченный рост числа клеток: N(t) при t 0 ; если к_} < к₂, то со временем популяция будет вымирать: N(t) 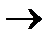0 при t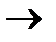 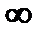, и только в частном случае при к_} = к₂ число клеток будет оставаться постоянным: N = N₍₎..

Динамику биологических процессов можно описывать уравнениями, аналогичными уравнениям химической кинетики. Однако по сравнению с обычной химической кинетикой биологическая кинетика характеризуется следующими особенностями.

1. В качестве переменных выступают не только концентрации веществ, но и другие величины.

2. Переменные изменяются не только во времени, но и в пространстве.

3. Биологическая система пространственно гетерогенна, и условия взаимодействия реагентов могут быть различны в разных точках системы.

Существуют специальные механизмы саморегуляции, действующие по принципу обратной связи.

Основная задача в биофизике сложных систем состоит в том, чтобы получить характеристики различных динамических режимов и выяснить условия и значения параметров, при которых они реализуются в живой клетке.

В биологических системах процессы, как правило, существенно нелинейны. Так, скорость простейшей бимолекулярной реакции второго порядка описывается математически в виде произведения концентраций реагентов, то есть в модели такой реакции правые части уравнений содержат нелинейные члены. В этом случае нахождение точных аналитических решений встречается с серьезными математическими трудностями и подчас вообще невозможно. Поэтому основной подход в современной кинетике и матема­тическом моделировании биологических процессов заключается в отказе от нахождения точных аналитических решений дифференциальных уравнений. Идея состоит в получении качественных характеристик динамического поведения системы: устойчивые и неустойчивые стационарные состояния, переходы между ними, колебательные режимы, качественная зависимость поведения системы от критических значений параметров. Наиболее важным свойством стационарного состояния является его устойчивость. Эта устойчивость определяется способностью системы самопроизвольно возвращать­ся в стационарное состояние после внесения внешних возмущений, отклоня­ющих систему от исходной стационарной точки.

Существует простой метод определения устойчивости стационарного состояния, которым мы воспользуемся без доказательства при исследовании моделей биологических процессов. Знак производной правой части диффе­ренциального кинетического уравнения в стационарной точке указывает на характер устойчивости этого стационарного состояния.

В сложной системе могут протекать реакции второго и более высоких по­рядков. Это соответствует тому, что наша система может обладать несколь­кими стационарными состояниями.