Лекция 9. Многомерные автоматические системы. Оптимальное управление

Как уже рассматривалось ранее, объект управления в общем случае может быть многомерным и представлен схемой рис. 81, где х₁…х_п – управляющие воздействия на объект (входные переменные), у₁…у_п – управляемые величины (выходные переменные) и f₁…f_п – внешние воздействия (возмущения).

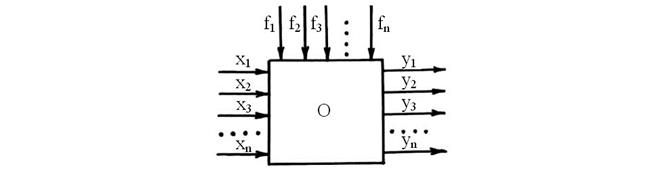
Рис. 81.

Для многомерных систем принята матричная форма записи. Под матрицей в рассматриваемых случаях понимается упорядоченная, т. е. выполненная по определенному правилу, табличная форма записи цифр, буквенных коэффициентов и т. п. Главным преимуществом матричной формы записи является возможность трансформировать в матричную форму не только запись переменных, но и операции над ними. Если физическая размерность переменных х (или у, f ) одинакова, то их можно записать в виде матриц-столбцов:

, , .

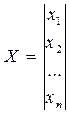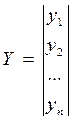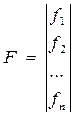Физические величины х₁…х_п, у₁…у_п и f₁…f_п, таким образом, могут трактоваться как проекции на оси координат некоторого вектора, т. е. матрица-столбец отождествляется с этим вектором.

Если физическая размерность у переменных разная, то переход от матрицы-столбца к вектору может быть осуществлен, если ввести весовые коэффициенты, уравновешивающие размерности отдельных составляющих. Однако такой переход не является единственным и имеет бесконечное количество вариантов, так как все х, у, f взаимосвязаны.

Если физическая размерность одна или приведена, то можно получить уравнение подобное уравнению для одномерных систем в операторной форме:

Y(p) = W(p)·X(p) + W_f(p)·F(p),

где Y(p), X(p), F(p) – матрицы-столбцы у, х и f; W(p) – матрица передаточных функций объекта; W_f(p) – матрица передаточных функций возмущений.

При отсутствии внешних возмущений можно записать:

Y(p) = W(p)·X,

т. е. то же, что и для одномерных систем, но в матричной форме. Отсюда следует, что структурная схема для многомерной системы аналогична схеме для одномерной. Широкие стрелки на схеме означают многомерность величин, рис. 82.

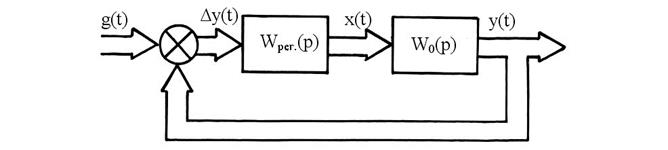
Рис. 82.

Использование матричного представления объекта эффективно при анализе и синтезе системы по динамическим показателям. Для этих целей разработан метод пространства состояний. Под переменными состояния и образуемым ими пространством состояния понимают совокупность величин, позволяющих по известным входным сигналам определить выходные. В качестве переменных состояния принимают как выходные переменные, так и их производные. Таким образом, по аналогии с одномерными системами и объектами выражение

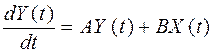
есть векторно-матричное уравнение состояния, где Y и X – матрицы-столбцы неизвестных выходных функций и задающих входных воздействий соответственно, а А и В – матрицы коэффициентов при переменных.

Возможность представления динамических процессов через состояние системы, которому соответствует точка в евклидовом пространстве, позволяет получить решение во временной области в виде траекторий движения этой точки. В этом случае исследование систем автоматического регулирования можно вести с помощью решения уравнений числовыми методами на ЭВМ.

Кроме вышеописанных, в качестве переменных состояния могут быть взяты величины ошибок от заданных значений, которые также полностью определяют состояние системы. Эти величины называют фазовыми координатами. Для многомерных систем в этом случае будет также матричная запись. Могут быть взяты и другие группы переменных состояния.

Для линейных стационарных систем может быть введено понятие переходной матрицы, отражающей временную реакцию выходов на единичные скачки на входе. В случае подачи на входы регулярного импульсного сигнала может быть получена матрица весовых коэффициентов, или весовая матрица. Все эти приемы похожи на используемые при анализе одномерных систем.

Специфическим для многомерных систем является возможность неравенства числа входов и выходов системы. Обычно п_у ≤ п_х, кроме этого существует взаимное влияние каналов друг на друга, которое может быть естественным или вводится искусственно для коррекции.

При анализе можно также использовать частотные методы. Если на один из входов многомерной системы подать гармонический сигнал с частотой ω, то на всех выходах появляется гармонические сигналы той же частоты, но с разными амплитудами и фазами. Таким образом, может быть введено понятие собственной и несобственной амплитудо-фазовой характеристики. Дальнейший анализ может производиться так же, как и у одномерных систем.

Самостоятельной проблемой многомерных систем и объектов является выбор исходной модели. До анализа модели неизвестна значимость отдельных входов и выходов для решения поставленной задачи управления. Трудно оценить, все ли входы (исполнительные устройства технологической установки) существенно влияют на выбранные выходы (технологические параметры). Поэтому вводится понятие полностью управляемой системы и полностью наблюдаемой.

Если все выходы системы зависят от всех входов или если нет переменных состояния, не связанных с выходными величинами, то такая система полностью управляемая. В ТАУ это звучит так: система управляема, если существует такое управление Х(t), которое переводит изображающую Y(t) точку из любой области пространства в начало координат (или более широкое понятие – в другую точку).

Если по выходным сигналам можно определить начальное (предыдущее) состояние системы, то она полностью наблюдаема. Оба вышеизложенных положения имеют математические доказательства, лежащие за пределами данного курса.

Более сложной задачей в технике (как для одномерных, так и для многомерных систем), чем автоматическое регулирование и управление, является оптимальное управление. Оно обеспечивает наиболее выгодный компромисс при минимизации трех компонентов технологического процесса: материала, энергии и информации. Критерии оптимальности могут быть различны. Критерии по различным затратам обычно не совпадают, поэтому выбирают какой-либо основным. Задачи оптимизации решаются на стадии проектирования комплекса «технология – оборудование – система управления». Связь между характеристиками технологического процесса и критерием его эффективности называют целевой функцией:

F = f(у₁…у_п; х₁…х_п),

где у₁…у_п – управляемые координаты; х₁…х_п – управляющие воздействия.

Если у_i = f(х₁…х_п), то и F = f(х₁…х_п).

Если целевая функция имеет экстремальный характер, то задача управления – находиться вблизи к экстремуму. Такое управление называется экстремальным. Если экстремум F лежит за пределами технологической области, то задача управления – вести процесс на границе этой области. Такое управление называется предельным.

Если F независимо от возмущений (F не зависит от t), то это – статическая оптимизация. Если же требуется такое управление, когда система должна выбирать наивыгоднейшую траекторию перехода из одного состояния в другое, то это – динамическая оптимизация. В последнем случае реализация такого управления возможна лишь с помощью ЭВМ.