Лекция 4. Управление в системах с путевым контролем
В машиностроении широко используются автоматические устройства, обеспечивающие заданную последовательность работы различных механизмов. Особенно распространены так называемые системы с путевым контролем, алгоритм функционирования которых содержит предписание выполнять цикл операций, каждая из которых начинается лишь после окончания предыдущей. Эти системы работают по принципу передачи команд, выполнение которых фиксируется с помощью путевых (конечных) выключателей. Контакты путевого выключателя замыкаются или размыкаются, отключая исполнительное устройство после выполнения какой-либо операции, связанной с перемещением инструмента или с заданным временем исполнения, и подключают цепи управления следующего. Для подключения различных приводов в машиностроении используют кроме конечных выключателей электромагнитные реле и подобные им устройства. Формализовать их работу можно с помощью алгебры логики (алгебры Буля). В этой алгебре принята двоичная система исчисления, а переменные и функции могут принимать лишь два значения: «0» и «1». Используется это следующим образом. После прихода сигнала управления цепь замкнута – 1, разомкнута – 0, т. е. соответствует работе включающе-выключающих релейных устройств.
Функции алгебры логики задаются таблицами истинности, в которых указываются все варианты сочетания переменных и соответствующей функции, и могут быть интерпретированы релейно-контактными схемами. Основные из них (табл. 1) имеют одну или две переменных.
Таблица 1
Функция
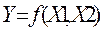
| Таблица истинности | Содержание логической функции | Запись формулы в алгебре логики | Релейно-контактный аналог | Обозначение в схемах | ||||||||
| Переменные | |||||||||||||
| Х1 Х2 | |||||||||||||
| Значение функции | |||||||||||||
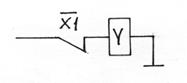
| Инверсия НЕ | У | Отрицание НЕ (функция одного переменного) у = 0, если х1 = 1 |
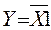
| 
| 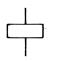
| обмотка реле | |||||||
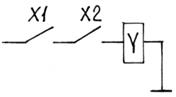
| Конъюнкция И | У | У = 1, если х1 = 1 и х2 = 1 |
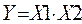
| 
| 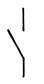
| замыкающий контакт | |||||||
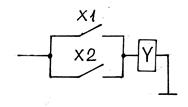
| Дизъюнкция ИЛИ | У | У = 1, если х1 = 1 или х2 = 1 |
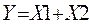
| 
| 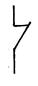
| замыкающий контакт | |||||||
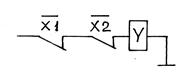
| Стрелка Пирса ИЛИ – НЕ | У | У = 0, если х1 = 1 или х2 = 1 |
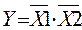
| 
| 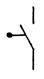
| путевые выключатели замык. и разм. | |||||||
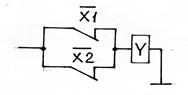
| Штрих Шеффера И – НЕ | У | У = 0, если х1 = 1 и х2 = 1 |
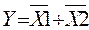
| 
| 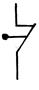
| ||||||||
| |
Таблица 2
| Закон алгебры логики | Релейно-контактная интерпретация |
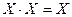
| 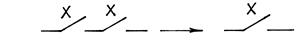
|
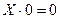
| 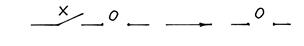
|
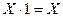
| 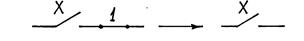
|
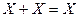
| 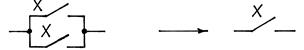
|
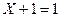
| 
|
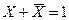
| 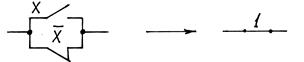
|
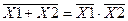 ИЛИ – НЕ ИЛИ – НЕ
| 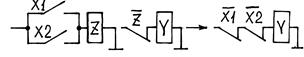
|
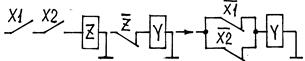
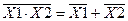 И – НЕ И – НЕ
| 
|
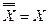
| 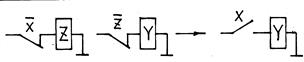
|
Таким образом, запись
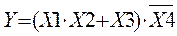
означает релейно-контактную схему (рис. 27).

Рис. 27.
В алгебре логики справедливы все действия обычной алгебры: перестановки, распределения, сочетания, скобки и т. д. (дополнительно см. табл. 2). Исходя из вышесказанного, в алгебре логики возможны преобразования и сокращения.
Например:
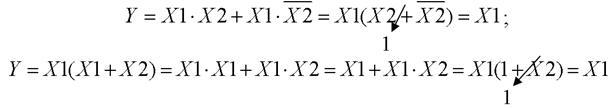
С помощью алгебры логики можно построить электрическую схему (осуществить синтез схемы) для работы заданного устройства. Для этого составляется описание работы устройства (вербальная модель) и на основании его таблица истинности.
Пример 1.
Электромагнитный клапан Y включается при определенном сочетании сигналов с трех контактных датчиков X1, X2, X3, которое отражено в таблице истинности:
| X1 | ||||||||
| X2 | ||||||||
| X3 | ||||||||
| Y |
Для составления структурной формулы работы Y необходимо выписать значения переменных в виде произведения из строки, где Y=1, а строки записать в виде слагаемых (так называемая совершенная дизъюнктивная нормальная форма СДНФ). Таких строк в таблице истинности две, т. е. два слагаемых по три переменных, умноженных друг на друга:
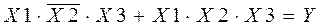 ,
,
преобразуя которую, получаем:
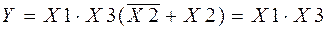 .
.
Таким образом, схема включения клапана Y:

С помощью алгебры логики можно сократить количество контактов. Без преобразования – 6 (первоначальная запись), после – 2, т. е. можно избежать непреднамеренного усложнения схемы.
Кроме вышеописанного алгебраического метода, требующего определенных навыков особенно при большом количестве переменных, для синтеза схем с путевым контролем используют более простой метод карт Карно совместно с построением графов функционирования. Поскольку рассматриваемые системы работают по циклу, то каждый элемент может иметь не менее двух состояний (включен и выключен) или любое четное число (тоже многократно). Если все механизмы определены и имеется словесное описание алгоритма функционирования, то для составления принципиальной электрической схемы, которая может быть реализована на электромагнитных реле или бесконтактных электронных элементах (логические элементы), необходимо составить граф функционирования.
Граф – это условная запись событий (в данном случае включение или выключение элемента), которые находятся во взаимосвязи. События обозначают заглавными буквами (вершины графа), а связи между ними – стрелками (ребра графа). Над ребрами указывают изменения входов-выходов. Стрелка, указывающая на событие, обозначенное буквой, – вход, а выходящая из него – выход.
Включение обозначается символом (буквой) без каких-либо дополнений (логическая 1), выключение тоже, но с чертой сверху (логическое отрицание, т. е. 0).
Пример 2.
В промышленной установке осуществляется возвратно – поступательное движение рабочего органа (РО) с помощью электродвигателя постоянного тока, подключаемого двумя электромагнитными реле К1 и К2 с помощью двух путевых выключателей s1 и s2 (рис. 28).
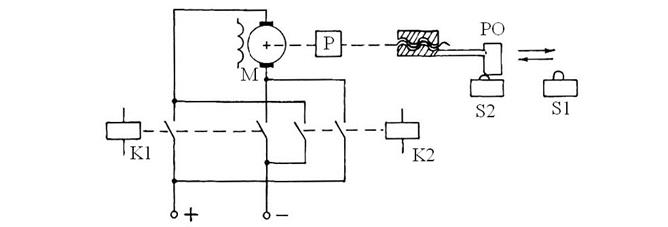
Рис. 28.
Последовательность работы схемы следующая. После подключения питания срабатывает реле К1 (событие) и включается контакт k1. Вследствие этого электродвигатель М перемещает рабочий орган (РО), s2 выключается, а s1 включается: k1, s1, s2 – изменения выхода, которые являются входными переменными для следующего события, изменяющиеся в той же последовательности, как это происходит в реальном времени.
Вышесказанное в виде графа записывается следующим образом:
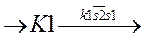
Далее К1 выключается и размыкается k1, затем включается К2 и замыкается k2, начинается обратное движение, при этом s1 выключается, а s2 включается. После возвращения РО в исходное положение К2 и k2 выключаются и все начинается сначала. Полностью граф будет выглядеть следующим образом:
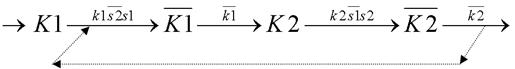
Построение схемы (синтез) осуществляется с помощью карт Карно, составляемых для вершин графа. Карта представляет собой прямоугольник, состоящий из квадратов, количество которых два в степени n, где n – число рассматриваемых для данной вершины переменных. Для одной переменной карта имеет вид, показанный на рис. 29, а, для двух – на рис. 29, б, и т. д.
а б
Рис. 29.
Клетки карты кодируются циклическим кодом Грея с помощью 0 и 1, обозначающих состояние переменных. В каждой клетке происходит изменение лишь одного разряда в сравнении с соседними (рис. 30, а, б, в, г).
В первую очередь на графе определяют начало цикла. В рассматриваемом примере нет смысла его менять, т. е. начало – это момент включения К1. После этого определяют существенные переменные для каждого события и строят для него карту Карно.
Для К1 существенными переменными, изменяющими его состояние (крайние обозначения на ребрах графа, входящих в К1), являются k2 и s1. Следовательно, имеем карту Карно из четырех квадратов (рис. 30, д) и К1 (k2,s1).
| х1,х2 | ||||||||||
| х3,х4 | ||||||||||
а б
Рис. 30.
| х2 | ||||||||||||
| х1, x2 | ||||||||||||
| х1 | х3 | |||||||||||
в г
| s1 | ||||
| k2 |
д
Продолжение рис. 30.
На начале цикла К1 (первое событие на графе) включено (1), а k2 и s1 выключены (0). Исходя из этого, в клетке, где k2=0 и s1=0, ставим 1 и отмечаем ее как начало цикла (рис. 31).
Далее двигаемся по циклу. Изменение k1 и s2 для К1 не имеет значения, поэтому следующее – s1; s1 включается (1), переходим в нужную клетку, а К1 выключается – ставим в этой клетке 0 (рис. 32).
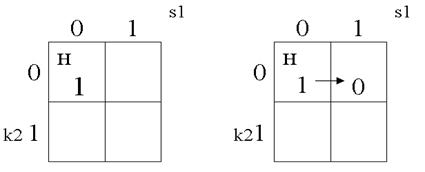
Рис. 31. Рис. 32.
Дальше k2 включается, а К1 остается выключенным (рис. 33). после этого s1 выключается, К1 остается выключенным (отмечаем на карте) и, наконец, k2 выключается и К1 включается (рис. 34).
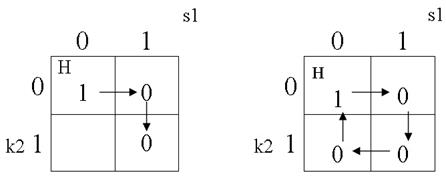
Рис. 33. Рис. 34.
Приходим в ту же клетку, из которой начали, получив тоже значение для К1. В каждой клетке только одно значение К1 (0 или 1), т. е. противоречий нет и можно приступать к построению схемы. Для этого в карте Карно выделяют подкубы – объединения клеток со значением К=1. В данном случае это одна клетка, но в общем случае может быть подкуб с числом клеток два в степени k, где k – число переменных. Это будет в том случае, если клеток со значением 1 несколько и они являются соседними, то есть такими, в которых при переходе из одной в другую происходит изменение состояния только одной переменной. В противном случае образуется несколько подкубов. Переменные, входящие в подкуб и не изменяющие своего значения в пределах этого подкуба, записываются в виде произведения значений, которые они имеют (0 или 1). Если подкубов несколько, то они образуют сумму произведений. В данном случае один подкуб. В клетке, где К1 равно 1, k2 и s1 равно 0. Таким образом, структурная формула для К1:
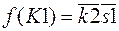 .
.
Произведение двух переменных в алгебре логики есть логическая операция «И», а с отрицанием – «ИЛИ – НЕ». На схеме это последовательное соединение двух замкнутых контактов (рис. 35).

Рис. 35.
Пример 3.
В той же установке после выключения К1 включается устройство, проводящее технологическую операцию ТО, которая задерживает включение К2 на 3 секунды и отключается после начала обратного движения.
График функционирования системы:
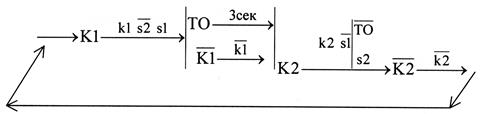
Выдержка времени в системе управления осуществляется с помощью различных реле времени КТ, имеющих контакт kt. С учетом этого граф будет выглядеть следующим образом:
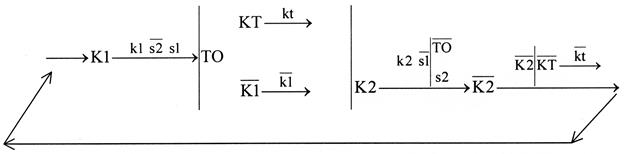
Для К1 построение схемы такое же, что и в примере 1. Для К2 три существенные переменные s2, k1,kt. Строим карту и отмечаем начало цикла.
В начале цикла (или в конце его – это одна и та же точка) К2, k1 и kt – 0, а s2 –1 (рис. 36).
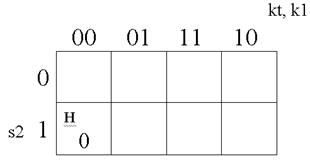
Рис. 36.
Перемещаясь по графу, принимая, что k1 срабатывает раньше, чем kt (это решает конструктор, если нет оговорок),заполняем карту (рис. 37).
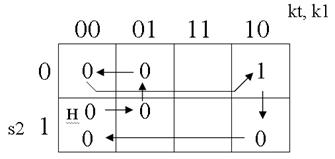
Рис. 37.
Рядом с клеткой, где s2=1, есть заполненные (неопределенные) клетки.
При объединении клеток в подкубы соблюдаются следующие правила.
1. Клетки карты со значением 1 должны быть включены хотя бы в один подкуб.
2. Подкуб должен объединять возможно большее число клеток (тогда минимально необходимое количество контактов).
3. Одна и та же клетка может быть включена в разные подкубы, если это способствует увеличению подкуба.
4. Размеры подкуба могут быть увеличены за счет включения в них клеток, которые оказались неуказанными (неопределенными).
Число подкубов должно быть минимальным.
Для данного случая в отличие от примера 1 необходимо учесть еще правило 4. Тогда подкуб будет включать в себя две клетки (рис. 38).
Структурная формула для подключения К2: 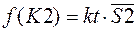 .
.
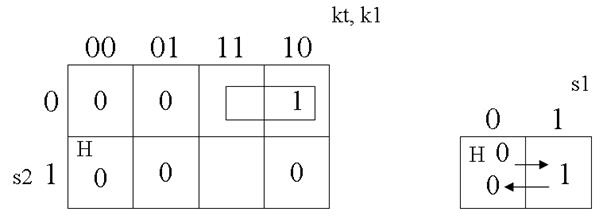
Рис. 38. Рис. 39.
Для ТО одна переменная - s1. карта для нее имеет две клетки (рис. 39). Структурная формула для ТО: f(ТО) = s1. В качестве самопроверки для КТ определить формулу самостоятельно.
Принципиальная схема системы управления показана на рис. 40.
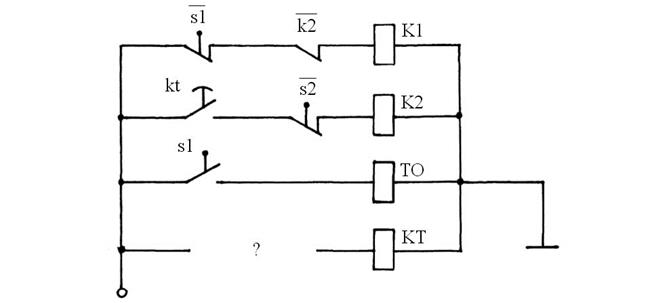
Рис. 40.
Пример 4.
Перемещение рабочего органа в отличие от предыдущих примеров происходит при помощи пневмоцилиндра, управляемого электропневмозолотниками с электромагнитами Y1 и Y2 (рис. 41).
По условию работы золотника электромагниты не могут быть включены одновременно, поэтому граф функционирования будет иметь вид
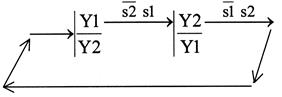
Начинаем построение с Y1. Для Y1 существенные переменные s1 и s2. Строим карту и осуществляем движение по циклу (рис. 41). на участке перехода от s1 к противоречие – в квадрате s2=0 и s1=0 два состояния вершины при одних и тех же значениях переменных.
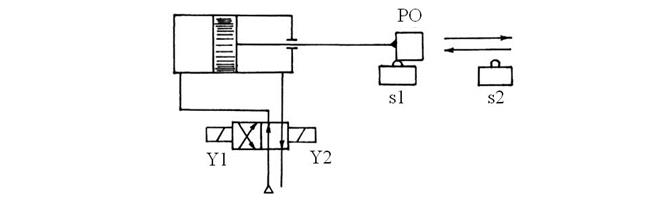
Рис. 41.
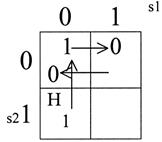
Рис. 42.
Отмечаем этот участок на графе линией сверху.
Для устранения противоречий существуют следующие правила.
1. К существенным переменным добавляем переменную, которая на участке противоречия изменяет свое значение нечетное число раз.
2. Если такой нет, то вводится элемент памяти – реле со своим контактом.
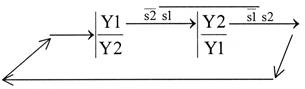
Для данного примера подходит правило 2. Вводим дополнительное реле Х, которое так же, как и другие элементы, должно иметь два состояния: одно – принимать на участке противоречия (Х), а противоположное – там, где это удобно, в данном случае в конце. С учетом вышесказанного переписываем граф.
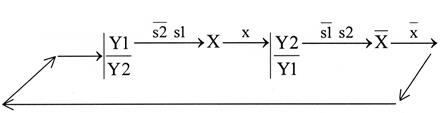
Теперь для Y1 существенная переменная х. Строим карту и определяем структурную формулу (рис. 43): f(Y1)= 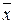 .
.
Аналогично для Y2: f(Y2)=X.
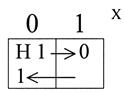
Рис. 43.
Для нового элемента Х существенные переменные s1 и s2. Строим карту и движемся по ней (рис. 44).
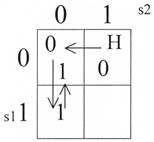
Рис. 44.
На участке осталось противоречие, но теперь имеется переменная х, изменяющаяся один раз.
Применяем правило 1. Строим карту для трех переменных для x = f(s1,s2,x) и двигаемся по графу (рис. 45).
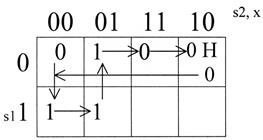
Рис. 45.
Согласно правилам выделения подкубов имеем два подкуба. Первый включает нижней горизонтальный ряд клеток, где s1=1, а второй состоит из двух вертикальных клеток со значениями s2=0 и х=1. Исходя из этого, структурная формула для Х
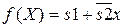 .
.
Теперь все вершины определены, строим принципиальную схему. Обмотки электромагнитов Y1 и Y2 имеют в своих цепях по одному контакту, а для Х путевой выключатель s1(замыкающий) подключается параллельно к цепи из двух последовательно включенных замкнутого путевого выключателя s2 и замыкающего контакта х. Принципиальная схема устройства показана на рис. 46
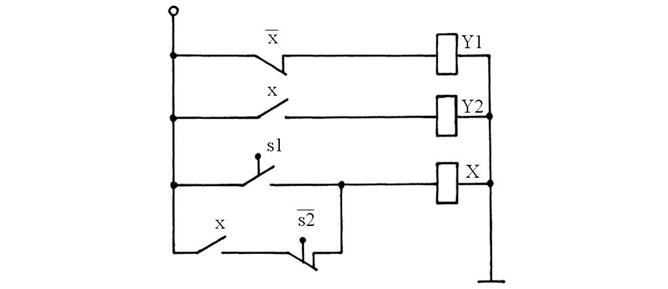
Рис. 46.
Для самопроверки постройте карту Карно и определите структурную формулу по таблице истинности примера 1.
Дата добавления: 2019-02-08; просмотров: 1465;











