Потоки заявок в СМО

Потоки заявок бывают входные и выходные.

Входной поток заявок – это временная последовательность событий на входе СМО, для которой появление события (заявки) подчиняется вероятностным (или детерминированным) законам. Если требования на обслуживание приходят в соответствие, с каким – либо графиком (например, автомобили приезжают на АЗС каждые 3 минуты) то такой поток подчиняется детерминированным (определенным) законам. Но, как правило, поступление заявок подчиняется случайным законам.

Для описания случайных законов в теории массового обслуживания вводится в рассмотрение модель потоков событий. Потоком событий называется последовательность событий, следующих одно за другим в случайные моменты времени .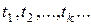

В качестве событий могут фигурировать поступление заявок на вход СМО (на вход блока очереди), появление заявок на входе прибора обслуживания (на выходе блока очереди) и появление обслуженных заявок на выходе СМО.

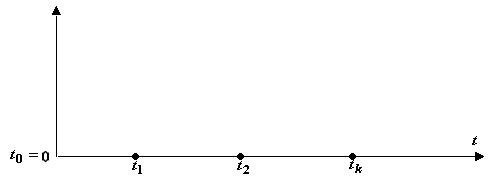
Потоки событий обладают различными свойствами, которые позволяют различать различные типы потоков. Прежде всего, потоки могут быть однородными и неоднородными.

Однородные потоки – такие потоки, в которых поток требований обладает одинаковыми свойствами: имеют приоритет первым пришел – первым обслужен, обрабатываемые требования имеют одинаковые физические свойства.

Неоднородные потоки – такие потоки, в которых требования обладают неодинаковыми свойствами: требования удовлетворяются по принципу приоритетности (пример, карта прерываний в ЭВМ), обрабатываемые требования имеют различные физические свойства.

Схематично неоднородный поток событий может быть изображен следующим образом

Соответственно можно использовать несколько моделей СМО для обслуживания неоднородных потоков: одноканальная СМО с дисциплиной очереди, учитывающей приоритеты неоднородных заявок, и многоканальная СМО с индивидуальным каналом для каждого типа заявок.

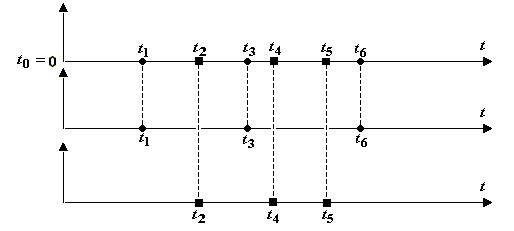
Регулярным потоком называется поток, в котором события следуют одно за другим через одинаковые промежутки времени. Если обозначить через 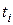– моменты появления событий, причем 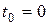, а через 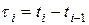интервалы между событиями, то для регулярного потока

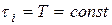
Рекуррентный поток соответственно определяется как поток, для которого все функции распределения интервалов между заявками

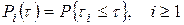
совпадают, то есть

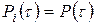
Физически рекуррентный поток представляет собой такую последовательность событий, для которой все интервалы между событиями как бы "ведут себя" одинаково, т.е. подчиняются одному и тому же закону распределения. Таким образом, можно исследовать только один какой-нибудь интервал и получить статистические характеристики, которые будут справедливы для всех остальных интервалов.

Для характеристики потоков очень часто вводят в рассмотрение вероятность распределения числа событий в заданном интервале времени 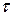, которая определяется следующим образом:

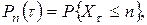
где 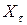– число событий, появляющихся на интервале .

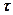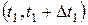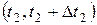Поток без последействия характеризуется тем свойством, что для двух непересекающихся интервалов времени и , где 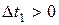, , 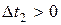, 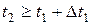вероятность появления числа событий на втором интервале не зависит от числа появления событий на первом интервале.

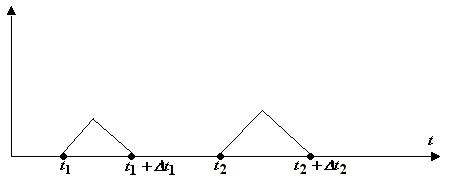
Отсутствие последействия означает отсутствие вероятностной зависимости последующего течения процесса от предыдущего. Если имеется одноканальная СМО с временем обслуживания 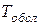, то при потоке заявок без последействия на входе системы выходной поток будет с последействием, так как заявки на выходе СМО не появляются чаще чем интервал 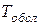. В регулярном потоке, в котором события следуют друг за другом через определенные промежутки времени, имеется самое жесткое последействие.

Потоком с ограниченным последействием называется такой поток, для которого интервалы 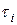между событиями независимы.

Поток называется стационарным, если вероятность появления какого-то числа событий на интервале времени 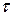зависит только от длины этого интервала и не зависит от его расположения на оси времени. Для стационарного потока событий среднее число событий в единицу времени постоянно.

Ординарным потоком называется такой поток, для которого вероятность попадания на данный малый отрезок времени dt двух и более требований пренебрежительно мала по сравнению с вероятностью попадания одного требования.

Поток, который обладает свойствами стационарности, отсутствия последействия и ординарности называют пуассоновским (простейшим). Этот поток занимает центральное место среди всего многообразия потоков, так же как случайные величины или процессы с нормальным законом распределения в прикладной теории вероятности.

Пуассоновский поток описывается следующей формулой:

,

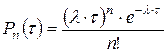где 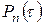– вероятность появления 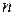событий за время 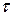, 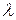– интенсивность потока.

Интенсивностью потока 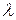называют среднее число событий, которые появляются за единицу времени.

Математическое ожидание и дисперсия пуассоновского потока находится из следующих соотношений:

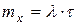
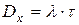
Для пуассоновского потока интервалы времени между заявками распределены по экспоненциальному закону

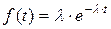
Потоком с ограниченным последействием, для которого интервалы времени между заявками распределены по нормальному закону, называется нормальным потоком.

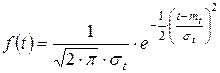
Естественным дальнейшим обобщением Марковских потоков (или вообще Марковских систем) являются полумарковские потоки, в которых отдельно и независимо задается матрица 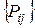вероятностей переходов из состояния 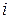в состояние 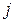и матрица 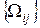вероятностей интервалов между событиям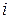и и .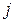

В частном случае

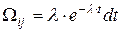
получаем простейший поток.