Структура и классификация СМО

Системы массового обслуживания – это такие системы, которые обслуживают массовый поток требований, при этом поток требований является случайной величиной.

В простейшем случае СМО может быть представлена в виде условной схемы, где изображены ее составные части.

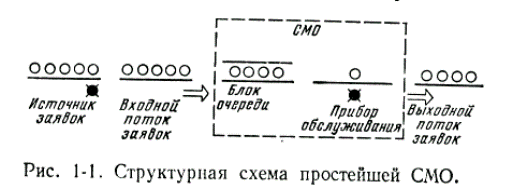
На этой схеме представлен источник заявок, который формирует входной поток, задерживая на какой-то отрезок времени поступление заявки в его состав. Заявки условно представлены шариками. Интервалы между заявками входного потока в общем случае неодинаковы: они представляют собой случайные величины и определяются вероятностными законами входного потока. Заявки поступают на вход блока очереди, в которой реализуется заданный закон дисциплины очереди. Этот закон определяет порядок обслуживания входных заявок (или их поступления на обслуживание), который может быть детерминированным (например, первой обслуживается та заявка, которая первой поступила, или первой обслуживается последняя поступившая заявка) или случайным (например, в соответствии с законом Эрланга).

Прибор обслуживания осуществляет обслуживание каждой поступившей на его вход заявки в соответствии с заданным детерминированным или случайным законом обслуживания. Обслуженная заявка поступает в выходной поток, который отличается от входного потока в зависимости от законов дисциплины очереди и обслуживания. Таким образом, в состав СМО входят два блока: блок очереди и прибор обслуживания.

Для модели СМО характерно, что все явления описываются с помощью событий, которые появляются в тот или иной момент времени (на временной оси). Входной поток заявок – это временная последовательность событий на входе СМО, для которой появление события (заявки) подчиняется вероятностным (или детерминированным) законам. Блок дисциплины очереди в соответствии с заданным вероятностным (или детерминированным) законом осуществляет выборку (или перераспределение) во времени (или на временной оси) событий во входном потоке для выдачи их на вход прибора обслуживания. Последний согласно своему закону осуществляет задержку во времени каждого поступающего на его вход события и формирует выходной поток заявок СМО. Идеализация модели СМО заключается в том, что все остальные свойства реальных систем, которые не вписываются в эту модель событий, не учитываются.

Примерами реальных систем управления, которые сводятся к моделям СМО, могут служить системы управления аэропортом, телефонной сетью большого города. При этом поток воздействий – случайная величина, так как интервалы между вылетами и посадкой самолетов, между вызовами абонентами телефонной станции, поступлениями заявок клиентов на обслуживание в сети бытового обслуживания и т.д. представляет собой случайные величины. Кроме того, время обслуживания самолета, разговора по телефону и обслуживания в предприятии бытового обслуживания также является случайной величиной.

Существует большое количество различных моделей СМО и методов их классификации.

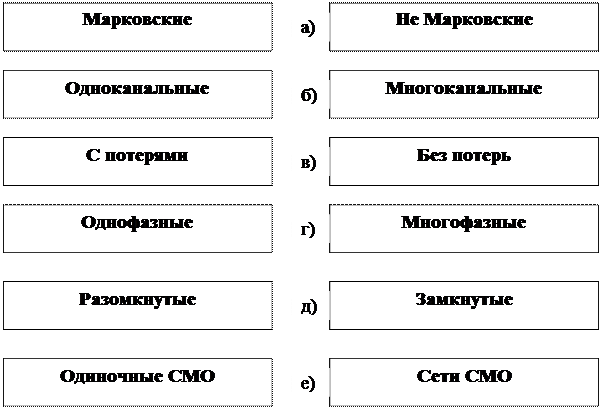
Рис. Классификация СМО

Прежде всего, они разделяются на Марковские и не Марковские.

СМО относятся к Марковским системам, если они описываются с помощью дискретных Марковских цепей. Аналитическому исследованию поддаются только частные случаи нелинейных СМО, которые выделяются в отдельные классы полумарковских, линейчатых и других СМО.

Далее СМО классифицируют на одноканальные и многоканальные в зависимости от числа приборов обслуживания, которые могут одновременно обслуживать входные заявки. При этом входной поток может быть один или их может быть несколько.

Системы массового обслуживания делятся на два типа: системы обслуживания с потерями и системы обслуживания без потерь.

Системы массового обслуживания с потерями – это такие системы массового обслуживания, в которых система отвечает отказом требованию, которое поступило в такой момент, когда все обслуживающие аппараты занятые, таким образом полностью отсутствуют условия для образования очереди.

Системы массового обслуживания без потерь – это такие системы, в которых требование, которое поступило, будет находиться в системе до тех пор, пока не закончится ее обслуживание. Система массового обслуживания без потерь имеет большое количество разновидностей, определяемых различными законами ожидания в очереди, дисциплиной очереди.

Для исследования последовательного процесса обслуживания несколькими приборами введена модель многофазной СМО, в которой заявка после обслуживания одним прибором поступает на следующий.

Далее можно ввести понятия разомкнутой и замкнутой СМО, в которой обслуженная заявка снова поступает на обслуживание. В современных системах управления встречаются такие сложные комбинации всех рассмотренных выше СМО, что они образуют целую сеть СМО.