Расчет на жесткость

Упругие перемещения валов влияют на работоспособность зубчатых передач, подшипников и различного вида соединений, вызывая концентрацию напряжений, интенсивное изнашивание, чем значительно усиливают опасность разрушения деталей. Поэтому при необходимости выполняют расчет на жесткость. Условие выполнения жесткости:

, ,

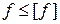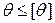где f – максимальный прогиб (стрела прогиба), мм; [f] – допустимый прогиб, мм;
θ – угол поворота сечения, рад; [θ] – допустимый угол поворота, рад.

Прогиб валов и углы поворота определяют известными методами, изложенными в курсе сопротивления материалов. С целью упрощения расчета можно использовать готовые формулы (табл. 8. 9).

Значения [f] и [θ] определяют, исхо­дя из опыта эксплуатации. Для участков валов с зубчатыми цилиндрически­ми колесами [f] = (0,01.... 0,03)m , с кони­ческими и гипоидными [f]= (0,005…0,007)m.

Здесь m – модуль зацепления, мм. В местах посадки зубчатых колес и в опорах скольжения [θ] = 0,001 (в ра­дианах), для радиальных шарикоподшип­никах [θ] = 0,005, для радиально-упорных роликовых подшипников [θ] = 0,0016, для шариковых сферических подшипников [θ] = 0,05.

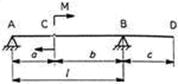
Таблица 8.4.9

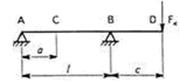
Формулы для расчета углов поворота сечений и прогибов двухопорных балок

Показатели жесткости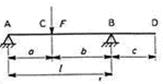
			-

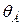
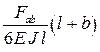
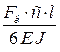
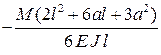
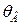
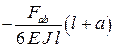
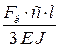
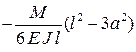
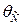
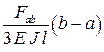
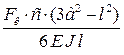
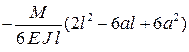
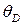
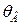
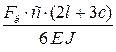
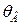
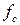
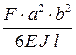
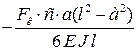
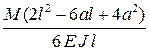
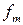
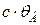
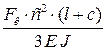
Ниже приведены примеры расчетов валов.

Пример 1. Рассчитать тихоходный вал цилиндрического косозубого редуктора на статическую прочность. Схема нагружения валов на рис. 8.4.1, 8.4.2.

Для расчета необходимы исходные данные, полученные в результате расчета передачи редуктора, а также должен быть произведен проектировочный расчет вала (т. е. определены все необходимые геометрические размеры вала).

Исходные данные:

Окружная сила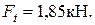

Радиальная сила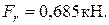

Осевая сила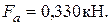

Вращающий момент на валу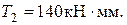

Диаметр делительной окружности колеса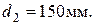

Консольная нагрузка на вал .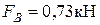

Частота вращения вала 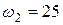1/с.

Материал вала – сталь 45.

Эскизная проработка вала представлена на рис. 8.4.3.

Решение

По табл. 3.1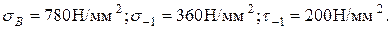

На основании рис. 8.4.1 и эскиза вала (рис. 8.4.3) составляется расчетная схема, определяются опорные реакции, строятся эпюры 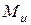изгибающих моментов и 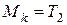крутящего момента (8.4.2).

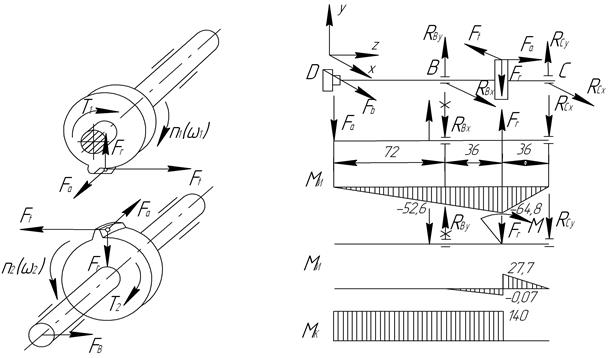
Рис. 8.4.1. Схема нагружения валов Рис. 8.4.2. Расчетная схема

1. Определим опорные реакции и строим эпюры в горизонтальной плоскости:

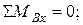
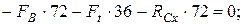
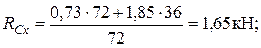
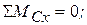
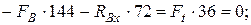
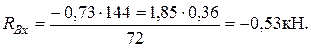
Проверка:

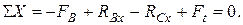
Изгибающие моменты в сечениях вала в горизонтальной плоскости:

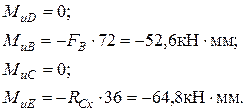
2. Опорные реакции в вертикальной плоскости:

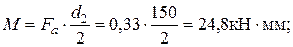
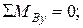
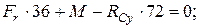
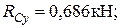
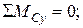
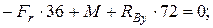
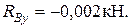
Проверка: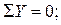

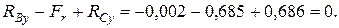
Изгибающие моменты в вертикальной плоскости:

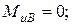
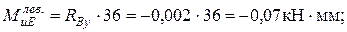
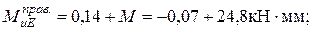
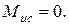
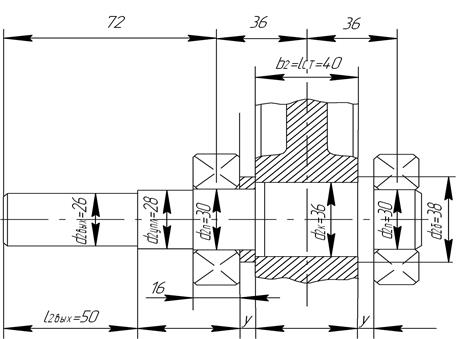
Рис. 8.4.3. Эскиз вала колеса

3. Строим эпюру крутящего момента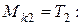

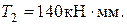
4. Проверяем прочность в опасном сечении на валу: сечение Е – опасное (см. эпюры изгибающих и крутящих моментов).

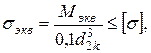
где 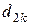(см. рис. 8.4.3).

[σ] = 50–70 МПа.

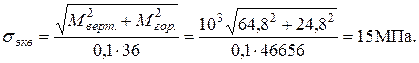
Так как 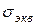< 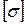, условие статической прочности выполняется.

Пример 2. Проверить тихоходный вал цилиндрического косозубого редуктора на сопротивление усталости (рис. 8.4.3).

Решение

1. Рассмотрим сечение вала, которое является концентратором напряжений – шпоночный паз (рис. 8.4.4). Материал вала – сталь 45.

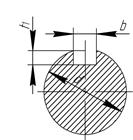Рис. 8.4.4. Шпоночный паз

По диаметру вала под колесом 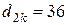по ГОСТ размеры шпонки 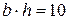(мм); 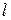– длина шпонки принимается в зависимости от длины ступицы 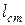колеса или ширины 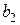зубчатого венца. В данном случае (рис. 8.4.3.) они равны.

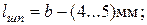
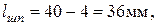
что соответствует ГОСТ; 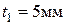- глубина паза вала.

По табл. 3.1 для стали 45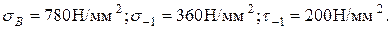

2. Определяем коэффициент запаса прочности по сопротивлению усталости:

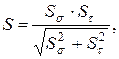
где 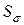– коэффициент запаса прочности – по нормальным напряжениям;

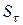– коэффициент запаса прочности – по касательным напряжениям;

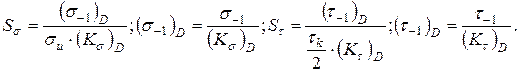
Коэффициенты концентрации напряжений

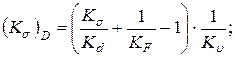
где 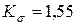- табл. 8.4.3; 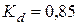- табл. 8.4.6; 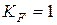- табл. 8.4.7;

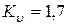- табл. 8.4.8;

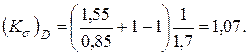
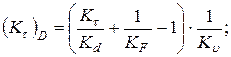
где 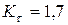- табл. 8.4.3; 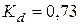- табл. 8.4.6; 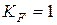– табл. 8.4.7;

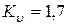– табл. 8.4.8.

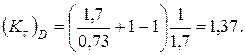
Предел выносливости в рассматриваемом сечении

.

.

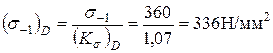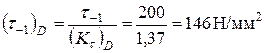Определим 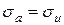и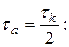

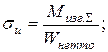
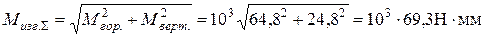(см. эпюры);

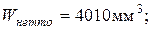
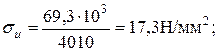
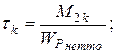
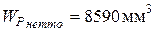(см. табл. 8.4.1);

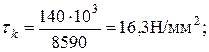
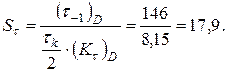
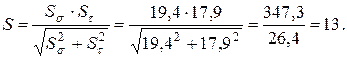
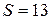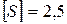> – условие прочности выполняется.

3. Определяем коэффициент запаса прочности в сечении, проходящем через т.В (напрессовка подшипника на вал).

Формулы для определения 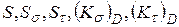(см. выше).

По табл. 8.4.4 для 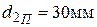находим отношения 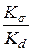и .

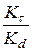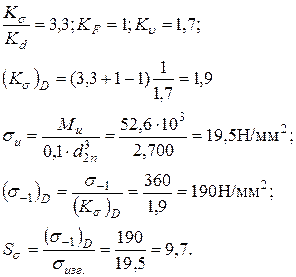
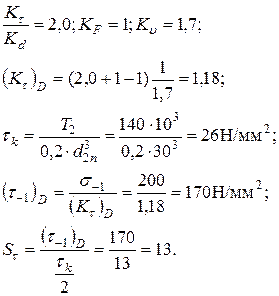
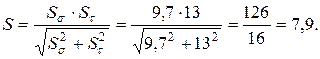
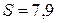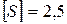> – условие прочности выполняется.

Пример 3. Рассчитать быстроходный вал конического прямозубого редуктора на статическую прочность (рис. 8.4.5) Для расчета использовать эскиз вала-шестерни (рис. 8.4.6).

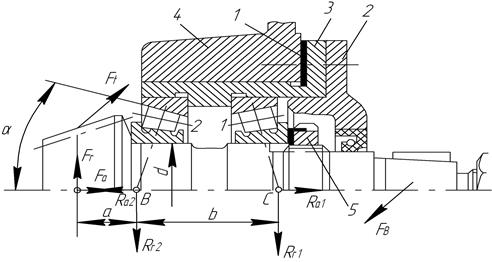
Рис. 8.4.5. Вал-шестерня конического редуктора: 1 – набор прокладок;

2 – крышка сквозная с манжетой; 3 – стакан; 4 – корпус;

5 – регулировочная гайка

Исходные данные:

Окружная сила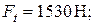

Радиальная сила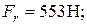

Осевая сила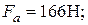

Консольная нагрузка на валу от соединительной муфты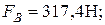

Вращающий момент на валу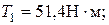

Допускаемое напряжение для стали 45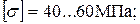

Средний делительный диаметр шестерни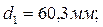

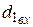– диаметр входного конца вала, мм;

– диаметр вала по уплотнение с крышкой, мм;

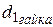–диаметр вала под регулировочную шлицевую гайку;

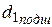– диаметр вала под подшипник;

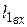– длина участка вала на входе (зависит от посаженной детали: шкиф, звездочка, полумуфта);

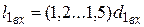– под шкив;

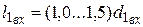– под полумуфту (зубчатое колесо);

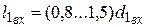– под звездочку.

Решение

Ориентировочно принимаем

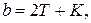
где 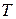– ширина подшипника, 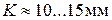– расстояние между торцами подшипников,

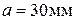– расстояние от середины длины зуба шестерни до торца подшипника.

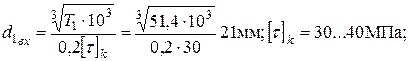
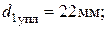ГОСТ 8752 – 79;

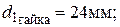ГОСТ 11871 – 80; М 24 x 1,5;

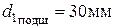(ориентировочно);

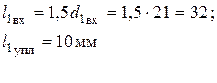– длина участка под уплотнение с крышкой;

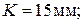
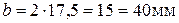(ширина подшипника 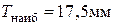– принята ориентировочно в зависимости от ).

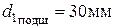С учетом зазоров и переходов с одного диаметра на другой примем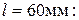

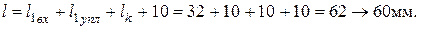
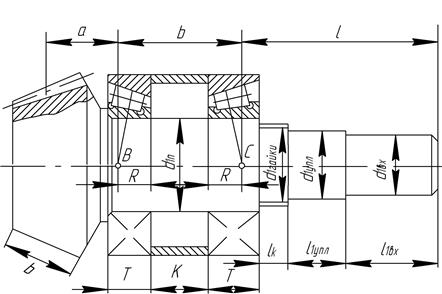
Рис. 8.4.6. Эскиз вала-шестерни

На основании рис. 8.4.5 и эскиза вала составляем расчетную схему, определяем опорные реакции, строим эпюры изгибающих моментов и крутящего момента с учетом

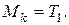
1. Определяем опорные реакции и строим эпюру изгибающих моментов в вертикальной плоскости:

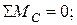
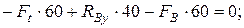
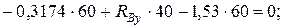
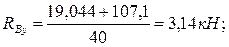
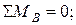
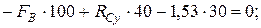
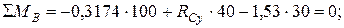
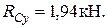
Проверка:

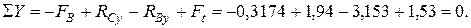
Определение изгибающих моментов:

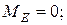
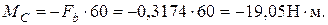
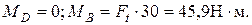
2. Определяем опорные реакции и построить эпюру изгибающих моментов в горизонтальной плоскости.

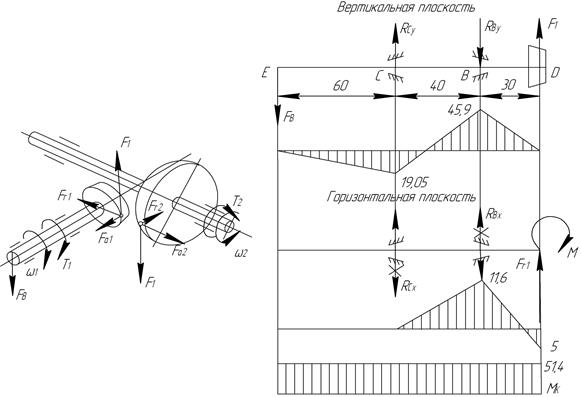
Рис. 8.4.7. Схема нагружения передачи

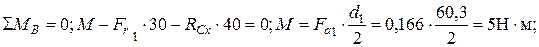
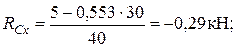
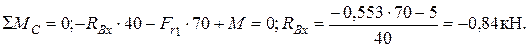
Проверка:

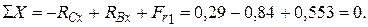
Определить изгибающие моменты:

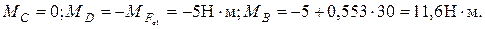
3. Строим эпюру крутящего момента:

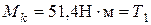
4. Проверяем прочность вала в опасном сечении В. Расчет ведем по максимальным касательным напряжениям.

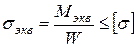– условие прочности.

<

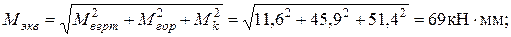
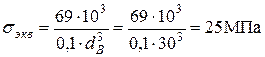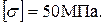
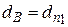
Условие статической прочности выполняется.

Пример 4. Рассчитать быстроходный вал конического редуктора на сопротивление усталости (рис. 8.4.5).

Решение

Рассмотрим сечение вала В, как более нагруженное. Концентратором напряжений является напрессовка подшипника на вал (сечение В).

Материал вала – сталь 45 без упрочнения. Механические характеристики стали:

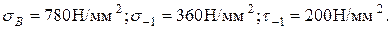
Коэффициент запаса прочности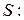

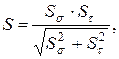
где 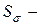коэффициента запаса прочности по нормальным напряжениям,

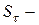коэффициента запаса прочности по касательным напряжениям

Определим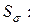

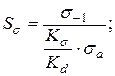
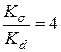(см. табл. 3.5);

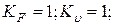
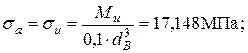
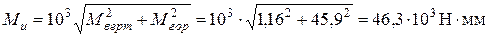(см. эпюры в задаче 3);

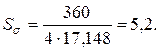
Определим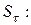

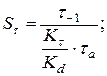
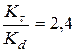(см. табл. 3.5);

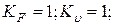
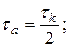
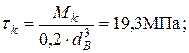
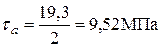(см. эпюру задачи 3);

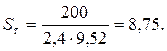
Определим коэффициент запаса прочности на усталостную выносливость:

>

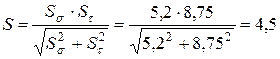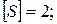
Фактический коэффициент запаса прочности больше допускаемого, т.е. условие прочности выполнено.