Ускорения точек плоской фигуры.

Для определения ускорения любой точки плоской фигуры найдем производную по времени от вектора скорости этой точки. Имеем согласно (2.17)

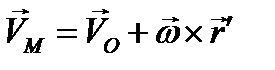
и, следовательно,

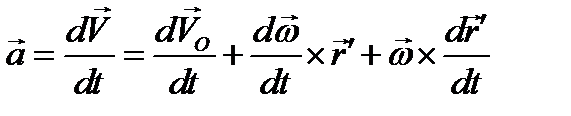(2.20)

Первое слагаемое 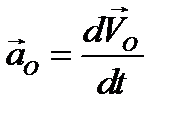одинаковое для всех точек фигуры полюса О', называется ускорением полюса. Второе слагаемое 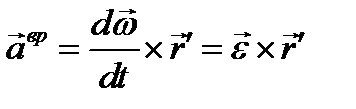называется вращательным ускорением. Здесь вектор 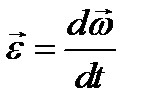представляет собой вектор углового ускорения. Вектор 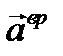перпендикулярен к 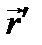и направлен в ту же сторону, что и враща­тельная скорость 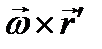точки плоской фигуры вокруг полюса, или в противоположную, сообразно тому, будет ли вращение фигуры ускоренным или замедленным; величина 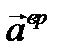равна

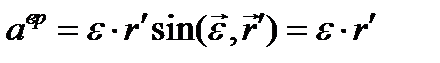
Третье слагаемое 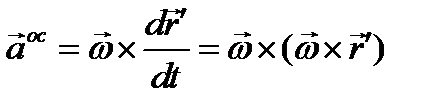. По известной формуле разложения двойного векторного произведения:

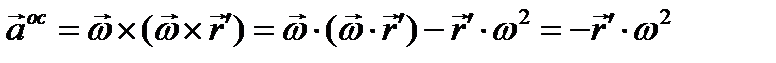
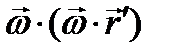=0, так как в скобках две ортогональных вектора. Эта составляющая ускорения, направленная от рассматриваемой точки к полюсу, называется осестремительным ускорением. Итак, имеем

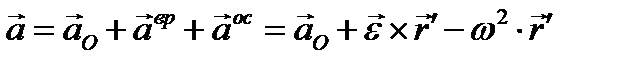(2.21)

т. е. ускорение любой точки в плоском движении может быть представлено как геометрическая сумма поступательного уско­рения, равного ускорению полюса, вращательного ускорения вокруг полюса и осестремительного ускорения к полюсу. На рис. 34 показан план ускорений плоской фигуры, за полюс выбрана точка

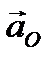
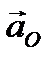
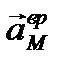
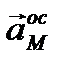
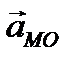
А

М

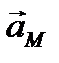
В

С

Рис 34

О, плоская фигура вращается вокруг полюса с угловым ускорением, направленным по часовой стрелке. Ускорение полюса 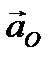одинаковое для всех точек фигуры, тогда как ускорение вращения зависит от расстояния до полюса. Складывая для каждой точки отрезка ОМ эти ускорения, можно получить ускорения любой точки плоской фигуры. На рис. 34 показаны ускорения точек, лежащих на отрезке ОМ, точек А,В,С и М, но отрезок ОМ проведён произвольно, следовательно, правило определения ускорений будет аналогично и для точек на любом отрезке, для любой точки плоской фигуры.

Глава 7.