Скорости точек плоской фигуры.

Продифференцируем по времени выражение (35)

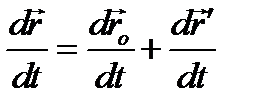(2.16)

В формуле (2.16) 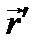постоянный по модулю вектор, следовательно, его скорость будет определяться угловой скоростью вращения плоской фигуры, формулой (2.13), и тогда скорость точки М может быть записана в виде

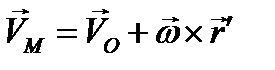(2.17)

Здесь 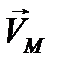- скорость любой точки плоской фигуры, 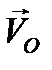- скорость выбранного начала системы координат ( в дальнейшем – полюс), жестко связанной с фигурой, 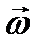- угловая скорость вращения плоской фигуры относительно оси, перпендикулярной плоскости фигуры и проходящей через точку О, и .

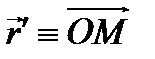О

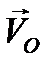
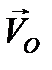
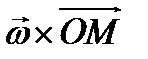
М

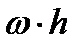
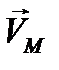
В

А

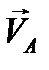
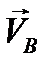
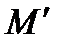
Рис 30

Поле скоростей плоской фигуры

На рис. 30 показано поле скоростей плоской фигуры, за полюс выбрана точка О, плоская фигура вращается вокруг полюса по часовой стрелке. Скорость полюса 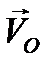(согласно 2.17) одинаковая для всех точек фигуры, тогда как скорость вращения зависит от расстояния до полюса. Складывая для каждой точки отрезка ОМ эти скорости, можно получить скорости любой точки плоской фигуры. На рис.30 показаны скорости точек, лежащих на отрезке ОМ, точек А,В,М, но отрезок ОМ проведён произвольно, следовательно, правило определения скоростей будет аналогично и для точек на любом отрезке, для любой точки полоской фигуры. Но остался невыясненным вопрос: зависит ли угловая скорость от выбора полюса? Пусть за полюс выбраны точки О и М, и пусть при этом угловые скорости будут разными.

,

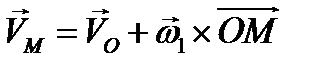
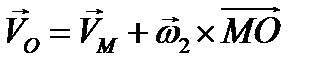Сложим эти два выражения

,

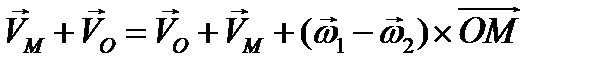откуда получаем 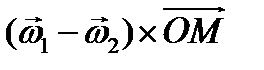=0 или 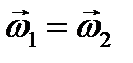, то- есть угловая скорость не зависит от выбора полюса, она является первым кинематическим инвариантом. Рассмотрим проекции скоростей фигуры на направление отрезка их соединяющих. Для этого умножим обе части выражения (38) на орт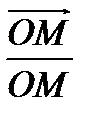

.

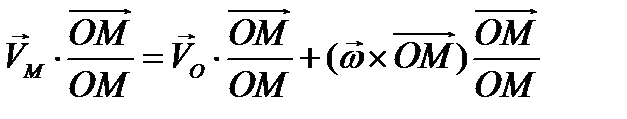Последнее слагаемое в полученном выражении равно нулю как смешанное произведение векторов с двумя равными векторами, то – есть

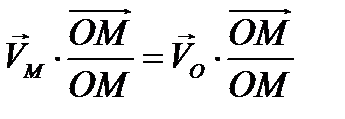
или 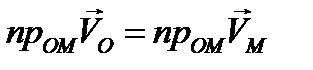. Проекции скоростей отрезков плоской фигурына направление этого отрезка равны. Это второй кинематический инвариант.