Определение положения твердого тела, имеющего неподвижную точку.

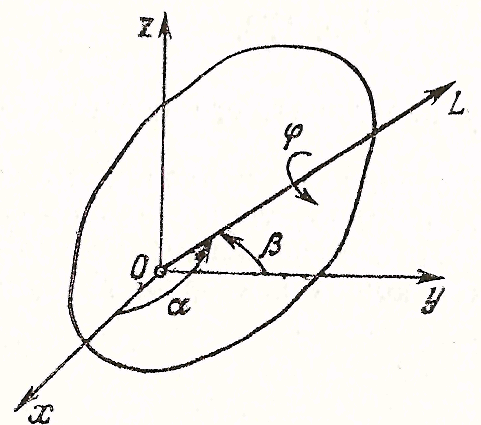
Обратимся к рассмотрению вращательного движения абсо­лютно твердого тела вокруг неподвижной точки. Вопрос этот имеет большое практическое значение, так как лежит в основе теории гироскопических явлений, ди­намики корабля, самолета, ракеты, а также движений небесных тел. Предположим, что рассматриваемое твердое тело имеет неподвижную точку (центр) О (рис. 35) и может

Рис. 35.

вращаться как угодно вокруг этой точки. Выясним, прежде всего, число величин, которое надо задать для определения положения твердого тела в пространстве. Для этого проведем через центр О ось OL, жестко связан­ную с телом; положение этой оси в пространстве определится двумя ве­личинами: углами α и β этой оси с осями Ох и Оу неподвижной системы координат. Но этих двух величин еще недостаточно для определения положения твердого тела, так как тело может вращаться около взятой оси. Задавая еще одну величину — угол φ поворота тела вокруг оси, - полностью фиксируем поло­жение тела в пространстве.

	x	y	z
x'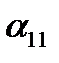
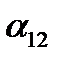
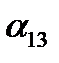
y'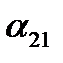
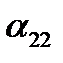
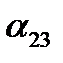
z'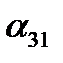

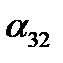
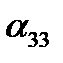
Итак, три величины должны быть заданы для определения положения тела, имеющего «неподвижной», системе Oxyz. Запишем таблицу косинусов углов между осями координат подвижной и неподвижной системами координат (буквами обозначены не углы, а их косинусы). Знание коэффициентов этой таблицы позволяет определить положение вращающегося тела относительно неподвижной системы координат. Как известно из аналитической геомерии, декартовы координаты точки в обеих системах связаны равенствами.

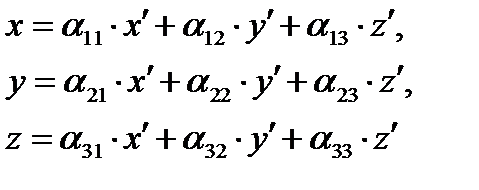(2.22)

Из девяти косинусов независимыми являются только три, так как они связаны между собой шестью независимыми соотношениями

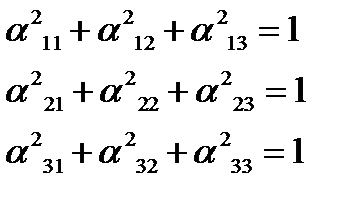
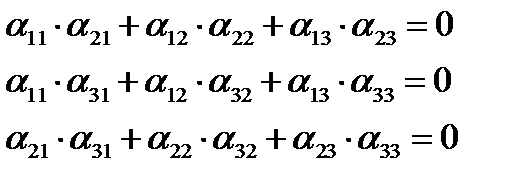
Выражение через три независимых ко-

синуса всех остальных затруднительно, так как требует решения системы уравнений второй степени.