Принятие решений в условиях неопределенности и риска

Как отмечалось выше, в условиях определенности каждому решению можно сопоставить единственный результат, который характеризуется определенной оценкой его эффективности, соответствующей выбранному критерию.

В условиях неопределенности каждое решение приводит к одному из целого множества возможных результатов, но вероятности появления этих результатов неизвестны. В этом случае отсутствует возможность оценить эффективность решения на основе объективных данных и ЛПР основывается на своих собственных субъективных предпочтениях. В данном случае элементами описания ситуации являются:

· множество возможных альтернатив действий ЛПР ;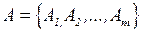

· множество возможных состояний внешней среды (множество гипотез) .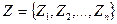

Предполагается, что на множестве отношений 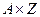можно задать некоторую функцию полезности (эффективности) 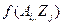, которая выступает в качестве оценки соответствующей альтернативы. Если множества A и Z конечны, то мера для оценки эффективности действий ЛПР представима в виде матрицы 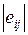, каждый элемент которой характеризует выбор альтернативы 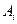при состоянии внешней среды 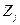. В этом случае решение ЛПР принимает с учетом субъективных предпочтений. Для решения задачи выбора альтернатив в условиях неопределенности применяется ряд критериев (принципов):

• максимина («осторожного наблюдателя», гарантированного результата, критерий Вальда);

• максимакса (критерий оптимизма);

• пессимизма-оптимизма (критерий Гурвица);

• минимального риска (критерий Сэвиджа);

•критерий Лапласа.

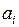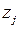Проиллюстрируем применение данных критериев на конкретном примере[2]. Рассматривается задача выбора одного из возможных трех программных продуктов для борьбы с одним из четырех типов внешнего воздействия н а информационную систему предприятия . Матрица эффективности 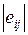представлена в табл. 6.12.

Критерий осторожного наблюдателя (Вальда).Это максиминный критерий,он гарантирует определенный выигрыш при наихудших условиях. Принцип заключается в выборе в качестве наиболее эффективной той альтернативы, которая имеет наибольшее среди наименее благоприятных состояний внешней среды зна-

Таблица 6.12

Матрица эффективности

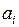
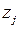
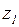
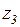
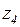
	0,1	0,5	0,1	0,2
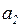
	0,2	0,3	0,2	0,4
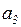
	0,1	0,4	0,4	0,3

чение эффективности. В каждой строке матрицы эффективности находится минимальная из оценок систем по различным состояниям среды. Таким образом, оптимальной считается альтернатива, для которой выполняется соотношение:

.

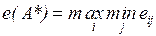Применение критерия максимина к нашему примеру дает следующие оценки:

е(а₁) = min(0,l; 0,5; 0,1; 0,2) = 0,1;

е(а₂) = min(0,2; 0,3; 0,2; 0,4) = 0,2;

е(а₃) =min(0,l; 0,4; 0,4; 0,3) = 0,1.

Оптимальное решение - система а_2.. Это – самая осторожная стратегия.

Критерий максимакса (критерий оптимизма).Этим критерием предписывается оценивать системы по максимальному значению эффективности и выбирать в качестве оптимального решения систему, обладающую эффективностью с наибольшим из максимумов. Альтернатива выбирается исходя из выражения:

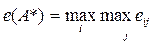
Оценки альтернатив на основе максимаксного критерия в нашем примере принимают такие значения:

е (а₁) = max (0,1; 0,5; 0,1; 0,2) = 0,5;

е (а₂) = max (0,2; 0,3; 0,2; 0,4) = 0,4;

е (а₃) = max (0,1; 0,4; 0,4; 0,3) = 0,4.

Оптимальное решение – система а₁.

Критерий пессимизма-оптимизма (Гурвица).Это критерий обобщенного максимина. Согласно данному критерию при оцен­ке и выборе систем неразумно проявлять как осторожность, так и азарт, а следует, учитывая самое высокое и самое низкое значе­ния эффективности, занимать промежуточную позицию (взвешиваются наихудшие и наилучшие условия). Для этого вводится коэффициент оптимизма α (0 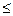α 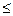1), характеризующий отноше­ние к риску лица, принимающего решение. Эффективность сис­тем находится как взвешенная с помощью коэффициента α сумма максимальной и минимальной оценок:

, .

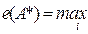
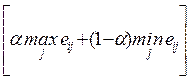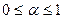Зададимся значением α = 0,6 и рассчитаем эффективность си­стем для рассматриваемого примера:

е(а₁) = 0,6 • 0,5+(1-0,6) • 0,1 = 0,34;

е(а₂) = 0,6 • 0,4+(1-0,6) • 0,2 = 0,32;

е (а₃) = 0,6 • 0,4+(1-0,6) • 0,1 = 0,28.

Оптимальной системой будет а₁ .

При α = 0 критерий Гурвица сводится к критерию максимина, при α = 1 - к критерию максимакса. Значение α может определяться методом экспертных оценок.

Критерий минимального риска (Сэвиджа).Минимизирует по­тери эффективности при наихудших условиях. Стратегия выбора характеризует те потенциальные потери, которые ЛПР будет иметь, если выберет неоптимальное решение. Для оценки альтернатив на основе данного критерия матрица эффективности должна быть преобразована в матрицу потерь (риска). Каждый элемент матрицы потерь определяется как разность между максимальным и текущим значениями оценок эффективности в столбце:

.

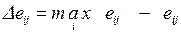После преобразования матрицы используется критерий минимакса:

.

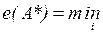
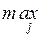
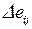Матрица потерь (матрица сожалений) приведена в табл. 6.13.

Таблица 6.13

Матрица потерь

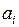
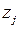
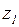
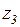
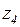
	0,1		0,3	0,2
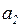
		0,2	0,2
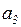
	0,1	0,1		0,1

е (а₁)= mах (0,1; 0; 0,3; 0,2) = 0,3;

е (а₂) = mах (0; 0,2; 0,2; 0) = 0,2;

е (а₃) = mах (0,1; 0,1; 0; 0,1) = 0,1.

Оптимальное решение - система а₃.

Критерий минимального риска отражает сожаление по поводу того, что выбранная система не оказалась наилучшей при определенном состоянии обстановки. Так, если произвести выбор системы , а состояние обстановки в действительности z₃, то сожаление, что не выбрана наилучшая из систем (а₃), составит 0,3.

Критерий Лапласа.Данный критерий применяется, если состояния внешней среды неизвестны, но их можно считать равновероятными. Решающее правило в этом случае имеет следующий вид:

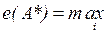
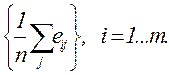
Рассчитаем эффективность систем по данному критерию для приведенного примера:

е(а₁) = 0,25 (0,1 + 0,5 + 0,1 + 0,2) = 0,225;
е(а₂) = 0,25 (0,2 + 0,3 + 0,2 + 0,4) = 0,275;

е(а₃) = 0,25 (0,1 + 0,4 + 0,4 + 0,3) = 0,3.

Оптимальное решение – система а₃.

Эффективность систем в неопределенных ситуациях может оцениваться по целому ряду критериев. На выбор того или иного критерия оказывает влияние ряд факторов:

• природа конкретной операции и ее цель (в одних операциях допустим риск, в других - нужен гарантированный результат);

• причины неопределенности (одно дело, когда неопределенность является случайным результатом действия объективных законов природы, и другое, когда она вызывается действиями разумного противника, стремящегося помешать в достижении цели);

• характер лица, принимающего решение (одни люди склонны к риску в надежде добиться большего успеха, другие предпочитают действовать всегда осторожно).

Возможны следующие практические рекомендации по применению рассмотренных выше критериев (принципов).

1. Критерий Вальда лучше всего использовать тогда, когда ЛПР желает свести риск от принятого решения к минимуму.

2. Коэффициент в критерии Гурвица выбирается из субъективных соображений: чем опаснее ситуация, тем больше ЛПР желает подстраховаться.

3. Критерий Сэвиджа удобен, если для ЛПР приемлем некоторый риск.

4. Критерий Лапласа может быть применен, когда ЛПР не может предпочесть ни одной гипотезы.