Ситуации формирования и выбора альтернатив
В центре методологии системного анализа находится операция формирования и сравнения альтернатив, которая выполняется с целью выбора альтернативы, подлежащей реализации. Любое решение может рассматриваться как выбор одного из нескольких возможных альтернативных вариантов. Процесс принятия решений - особый вид человеческой деятельности, направленный на выбор лучшей (или наиболее целесообразной) из имеющихся альтернатив.
Из общих признаков решений выделяются сложность и неопределенность, во многом определяющие выбор методов их разработки и принятия. Неопределенность характеризует информационные условия, в которых принимается решение. В зависимости от обеспеченности информацией лицо, принимающее решения (ЛПР) может оказаться в разных условиях: в условиях определенности, в условиях риска, в условиях неопределенности.
Решения классифицируются также в зависимости от того, принимаются ли они в одном структурном звене или в нескольких, учитывается ли один критерий[43] или решение принимается в условиях многокритериальности, является ли оно индивидуальным или групповым и т. п.
Рассмотрим ситуацию полной определенности, когда каждому возможному решению можно сопоставить единственный результат, который характеризуется определенной оценкой эффективности, соответствующей выбранному критерию. Для социально-экономических систем выделяют следующие ситуации выбора (принятия решений):
- однокритериальная ситуация выбора в одном относительно независимом структурном звене;
- однокритериальная ситуация выбора в системе нескольких звеньев;
- многокритериальная ситуация выбора в одном звене;
- многокритериальная ситуация выбора, возникающая по системе в целом, при которой выбор каждого отдельного структурного элемента характеризуется одним критерием;
- многокритериальная ситуация выбора, охватывающая целую совокупность звеньев, каждый из которых, в свою очередь, находится в многокритериальной ситуации выбора.
Необходимым признаком сложного решения является наличие нескольких несводимых друг к другу критериев. Таким образом, по сложности решения делятся на однокритериальные и многокритериальные.
1. Однокритериальные методы выбора. Считается известным:
• исходное множество альтернатив 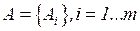 ;
;
• оценки результатов выбираемых альтернатив 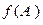 ;
;
• критерий выбора 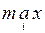
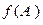 или
или 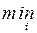
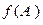 .
.
В процессе решения задачи определяется альтернатива А*, для которой 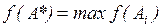 или
или 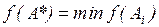 .
.
Большинство простых решений, принимаемых по одному критерию в условиях отсутствия неопределенности, могут быть формализованы. Другими словами, существует возможность построения адекватной математической модели, которая позволит принимать наиболее эффективные, иногда даже оптимальные решения.
2. Многокритериальные методы выбора. В достаточно большом количестве случаев принятия решений приходится учитывать не один, а несколько критериев.
Например, выбор интегрированной информационной системы предприятия осуществляется по многим критериям, в том числе, таким, как:
1. соответствие функций системы требованиям, выработанным в процессе анализа и построения информационной модели предприятия;
2. соответствие системы современным технологическим стандартам (архитектура клиент-сервер, используемые СУБД, возможность распределенной работы и интеграция с Интернет);
3. возможности системы по настройке и изменению;
4. уровень сложности сопровождения и администрирования;
5. адаптивность системы к конкретным условиям деятельности;
6. стоимость системы;
7. другие.
Объектом системного синтеза являются, как правило, многокритериальные решения со слабовыраженной структурой, не позволяющей построить адекватную формальную модель. Многокритериальность выступает как необходимый признак любого сложного решения, однако она может проявляться как следствие необходимости учета множества факторов в одном звене системы, либо необходимости согласования однокритериального выбора в нескольких звеньях, либо необходимости учета взаимосвязей элементов, каждый из которых обладает специфическим свойством целенаправленного поведения. Соответственно могут быть выделены сложные хозяйственные и управленческие решения разных типов.
Сложное решение первого типа соответствует многокритериальной ситуации выбора в одном звене хозяйственной системы.
Сложное решение второго типа соответствует многокритериальной ситуации выбора, возникающей по системе в целом, когда выбор каждого отдельного звена характеризуется одним критерием. Подобные решения возникают в условиях, когда между звеньями системы возникают отношения экономического подчинения.
Сложное решение третьего типа соответствует многокритериальной ситуации выбора, возникающей по системе в целом, при которой каждое отдельное звено системы также находится в многокритериальной ситуации выбора.
Каждому классу сложных решений обычно соответствует определенный характер и методы оптимизации. Множество подходов к моделированию оценки и выбора альтернатив следует сгруппировать по следующим основным признакам:
а) в зависимости от количества критериев оценки:
- однокритериальные оценки;
- многокритериальные оценки и процедуры;
б) в зависимости от класса методов:
- формализованные;
- экспертные;
- имитационные.
На рис. 6.9 представлена классификация ситуаций принятия решений в зависимости от количества критериев и фактора неопределенности.

Рис. 6.9. Классификация ситуаций принятия решений.
Рассмотрим соответствие между методами моделирования и классами хозяйственных решений, для которых они применяются.
В том случае, когда выделенный критерий позволяет сравнивать между собой все допустимые альтернативы решения и выбирается одна, являющаяся наилучшей, решение относится к типу оптимизирующих. В математическом отношении разрешение соответствующих проблемных ситуаций сводится к определению условного экстремума функции. Большинство из проблемных ситуаций этого типа требуют применения таких разделов прикладной математики, как линейное и нелинейное программирование, динамическое программирование и т. д. При применении этих методов для принятия простого решения структура целевой функции должна быть достаточно простой.
Реальные ситуации принятия решения даже в одном звене характеризуются достаточно сложной структурой целевой функции. Это связано с многообразием требований к системе. Так, как было показано, выбор информационной системы может различаться требованиями к надежности, стоимости, адаптивности и т. д. Данные требования могут быть противоречивы в том смысле, что удовлетворение одного из них может привести к невыполнению других. Необходим системный учет всех требований. Это приводит к качественному изменению структуры целевой функции.
Возникает ситуация принятия сложного хозяйственного решения. Если при этом находится доминирующая альтернатива, то проблемы выбора как таковой не существует, а именно данная альтернатива принимается в качестве оптимального решения. Однако доминирующие альтернативы на практике встречаются довольно редко. Поэтому приходится применять методы многокритериального выбора, причем решение должно быть наилучшим в определенном смысле. Это приводит к задаче векторной оптимизации, которая заключается в нахождении максимума вектор-функции:
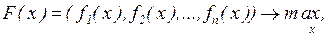
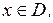
где D — область допустимых решений модели.
В случае многокритериальной оптимизации возникает ряд проблем, в частности, проблема с выбором принципа оптимальности. В математическом отношении эта проблема эквивалентна задаче упорядочения векторных множеств, а выбор принципа оптимальности – выбору отношений порядка. Вторая проблема связана с нормализацией векторного критерия F(x).Частные критерии имеют различные единицы измерения, поэтому их необходимо привести к единому масштабу измерения, т. е. нормализовать (обычно приводят к безразличным величинам). Третья проблема связана с учетом приоритета (степени важности частных критериев).
В многокритериальных ситуациях выбор оптимальной альтернативы по совокупности несводимых критериев в общем случае невозможен. Устанавливаются лишь допустимые альтернативы, а само решение относится к типу удовлетворяющих. В задаче многокритериального выбора решение почти всегда ищется в области компромиссов или в области решений, оптимальных по Парето.
Если имеется исходное множество вариантов, число которых более двух, то среди этих вариантов можно выделить подмножество, которое называется множеством недоминируемых вариантов или множеством эффективных вариантов по Парето. Варианты множества Парето обладают следующими двумяважными свойствами:
1. варианты множества Парето доминируют все остальные варианты исходного множества;
2. варианты внутри множества Парето находятся в противоречивых отношениях, и среди них нет доминирующих вариантов.
Критерий Парето: следует считать, что любое изменение, которое никому не причиняет убытков и которое приносит некоторым людям пользу (по их собственной оценке), является улучшением. Данный принцип применяется в ситуациях, когда оптимизация означает улучшение одних критериев при условии, чтобы другие не ухудшались.
Область компромиссов обладает тем свойством, что все принадлежащие ей решения не могут быть улучшены одновременно по всем локальным критериям. Таким образом, область компромиссов есть область потенциально оптимальных решений.
Известен целый ряд методов решения многокритериальных задач, которые можно разбить на следующие группы:
1. Сведение многих критериев к одному путем введения весовых коэффициентов для каждого критерия (более важный критерий получает больший вес).
2. Минимизация максимальных отклонений от наилучших значений по всем критериям.
3. Оптимизация одного критерия (почему-либо признанного наиболее важным), а остальные критерии выступают в роли дополнительных ограничений.
4. Упорядочение (ранжирование) множества критериев и последовательная оптимизация по каждому из них.
5. Поиск согласованного по некоторым правилам экспертного решения.
Очень часто задачу выбора пытаются решить на основе построения интегрального (обобщающего) критерия. Для этого используются разнообразные способы «свертки» показателей, т. е. построение различных обобщающих показателей, прежде всего, аддитивных и мультипликативных.
Аддитивный обобщающий показатель (критерий) получается как взвешенная сумма оценок по частным показателям (критериям).
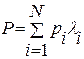 ,
,
где pi – значение i-го показателя (критерия);
li – вес (значимость) i-го показателя (критерия).
Мультипликативный обобщающий показатель строится как взвешенное произведение оценок по отдельным показателям.
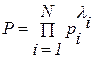 ,
,
где pi – значение i-го показателя (критерия);
li – вес (значимость) i-го показателя (критерия).
Общей особенностью данных обобщающих критериев является то, что они предусматривают возможность малой степени достижения одних целей за счет большей степени достижения других. При этом в оценке «стираются» различия отдельных критериев. Также проблемой является определение весов критериев.
В целом ряде ситуаций нежелательно сведение оценок объектов по разным критериям к одной, так как противоречивость критериев имеет существенное значение. Для преодоления этого недостатка исследователи стараются представить пространство критериев. Одним из возможных средств решения этой задачи являются различные графические представления альтернатив в пространстве критериев.
Сложные решения второго типа, возникающие по системе в целом, когда выбор каждого отдельного элемента характеризуется одним критерием, естественно приводят к удовлетворяющему типу поведения. Для таких решений принципиально невозможно сведение многих критериев в один. В данном случае целесообразно использование аппарата теории игр и статистических решений.
Наиболее проблемным является процесс оценки и выбора сложных решений третьего типа. Сложные решения третьего типа всегда основаны на динамических моделях, т. е. включают фактор времени. Одним из наиболее эффективных подходов к моделированию данных решений является имитационное моделирование. Имитация применяется в исследовании систем, позволяя экспериментально воспроизвести возможные последствия принятия решений о комбинации тех или иных решений и условий их реализации. Проблемы применения методов имитационного моделирования связываются, прежде всего, со сложностью разработки подобных моделей, а также значительными затратами времени и средств на их разработку. Особенности этих моделей заключаются в том, что они не выбираются из какого-либо определенного и хорошо разработанного класса моделей, а обычно строятся по соображениям адекватности описания закономерностей функционирования моделируемого объекта. Структура имитационных экспериментов обычно предусматривает участие в них экспертов, способных задавать значения параметров, не поддающихся определению статистическими или аналитическими методами.
Одним из направлений разрешения подобных сложных ситуаций выбора также является эвристическое программирование и логико-лингвистическое моделирование. Ценность эвристического программирования состоит, прежде всего, в том, что эвристическими методами часто могут быть получены «хорошие» решения для тех задач, для которых либо не существует алгоритмического решения, либо оно требует слишком больших затрат времени и средств. Эвристические методы основаны на глубоких профессиональных знаниях экспертов и применении экспертных систем. В то же время, основным недостатком существующих алгоритмических и эвристических подходов к сложным проблемным ситуациям является невозможность с их помощью дать полное отражение реальных условий принятия решений. Это положение носит принципиальный характер. Разнонаправленность хозяйственных интересов как основное противоречие рассматриваемой проблемной ситуации при использовании этих методов не разрешается, а «примиряется». Это – согласованное решение, вытекающее из компромисса и соответствующее возможностям компромисса.
Роль ЛПР в таких системах связывается с необходимостью предусмотреть и стимулировать появление качественно новых, творческих решений во всех взаимодействующих блоках. Подобный подход характерен, например, для экспертных систем, для гомеостатических системных моделей.
Помимо указанных одним из адекватных подходов к разрешению сложных ситуаций выбора является формирование специальных экспертных процедур, основанных на групповом выборе решений, одна из которых рассмотрена далее.
Дата добавления: 2020-11-18; просмотров: 995;











