Аналитическое счисление

Кроме графического в ряде случаев широко применяют аналитическое счисление: счислимое место получают вычислением его координат j_с, l_с по координатам начальной точки j_о, l_о и их изменениям РШ и РД, образующимся в результате плавания судна из этой точки:

; .

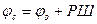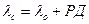Таким образом, задача сводится к вычислению РШ и РД в зависимости от направления и протяженности перемещения судна из начальной точки.

Рассмотрим на плоскости меркаторской проекции прямоугольник, образованный меридианом начальной точки М_о, параллелью искомого счислимого места М_с и линией пути – локсодромией длиной S между этими точками (рис. 1.25). Катеты этого треугольника – разность долгот РД и разность меридиональных частей РМЧ – выражены в одинаковых единицах длины – экваториальных милях (единицах карты) и поэтому

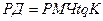
Рис. 1.25.

Обычно применяют приближенные, но более простые формулы.

;

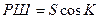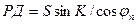
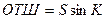
На практике при плавании по локсодромии разность широт РШ обычно невелика; даже большие переходы в океане осуществляют по участкам локсодромий. Это позволяет решать задачу на сфере с приближенной заменой промежуточной широты j_п на среднюю

.

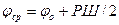
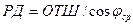Дрейф с углом a прости учитывают тем, что в расчетных формулах вместо a подставляют ПУ_a = ИК + a. Действие течения за время счисления t учитывают по тем же формулам как дополнительное плавание S_Т = V_Т ^, t по направлению К_т, циркуляцию также учитывают как дополнительное плавание d по промежуточному курсу К_пр = ИК 1+q.

Аналитическое счисление разделяют на простое и составное.

Простое счисление - когда курс, дрейф и течение неизменны.

Составное счисление - когда плавание состоит из участков локсодромий протяженностью S_i курсами K_i. В таких случаях расчеты несколько упрощают тем, что найденные, как описано выше, по участкам РШ_i и ОТШ_i суммируют, получая генеральные значения:

; ,

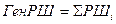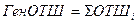а затем один раз Ген ОТШ переводят в Ген РД, после чего по формулам получают счислимые координаты.

При использовании электронных карт, при частом маневрировании, что характерно для ледового плавания, для деятельности промыслового и военного флотов, необходимо автоматически непрерывно вырабатывать счислимые координаты судна и вычерчивать его счислимую траекторию на карте (или дисплее).

В качестве исходных данных для счисления в автопрокладчик непрерывно и автоматически поступают курс от гирокомпаса и скорость от лага. Поправку компаса DГК, коэффициент лага К_л, угол дрейфа a и элементы течения К_Т и V_Т, а также координаты начальной точки j_о и l_о устанавливают или изменяют вручную.

Счисление на персональном компьютере ведется для "дискретного времени" на моменты t_i=t₀+iDt, где i = 1, 2, …, а Dt – малый интервал времени, например 2с. На моменты t_i автоматически снимаются показания гирокомпаса и лага и на эти же моменты вычисляются счислимые координаты j_i, l_i по преобразованным формулам аналитического счисления:

;

,

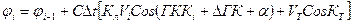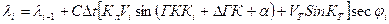где j, l и их приращения вычисляются в минутах, С – коэффициент масштаба и согласования размерностей. Текущая счислимая широта j_i выводится как результат на дисплей, печать и т.п. и одновременно используется для вычисления l_i по второй из этих формул.

Точность счисления

Точность счисления зависит, естественно от погрешностей исходных данных. Как бы ни велось счисление, графически, аналитически или автоматически, его всегда можно представить вектором перемещения судна длиной S по направлению ПУ. В соответствии с этим все погрешности исходных данных можно сгруппировать на продольные – вдоль линии пути и поперечные – обусловленные погрешностями ПУ.

Продольная средняя квадратическая погрешность счисления, обусловленная такой же погрешностью m_кл принятого коєффициента лага К_л и пропорциональна плаванию S = Vt: .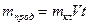

Аналогично этому, поперечная средняя квадратическая погрешность счисления выражается через такие же погрешности принятых поправки компаса m_Dк и угла дрейфа m_a: .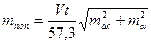

Средние квадратические погрешности направления m_кт и скорости m_vт течения, которое учитывают (или не учитывают, но оно действует) вызывают погрешности счисления и продольные и поперечные.

Все перечисленные погрешности счисления взаимонезависимы и поэтому их совместное действие находим по правилу сложения дисперсий, что дает круговую среднюю квадратическую погрешность счисления М_с(t) за время t:

,

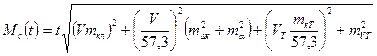где: m_DГК » 0,7°;

m_DМК » 1,2°;

m_a » 1,5°;

m_кл » 1%;

m_кт » 15°-20°;

m_vт » 15%¸20%.

В течение времени счисления t (часы), пока условия плавания практически неизменны, сохраняется постоянным значение корня в последней формуле, которое обозначим К_с, а формулу представим в таком виде

,

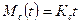где К_с – коэффициент точности счисления, мили/час.

При длительном счислении без коррекции погрешности исходных данных частично компенсируются при t > 2 ч .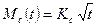

Важно помнить, что погрешность счислимого места М_см (t) складывается из погрешностей начальной точки М_о и погрешности счисления М_с (t) за время его ведения t:

.

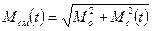Для оценивания коэффициента точности счисления К_с по результатам независимых от счисления определений места судна (обсерваций) используют выявляемые при этом невязки.

Невязкий называют вектор С между одновременными счислимой и обсервованной точками. Этот вектор выражают направлением относительно меридиана на обсервованную точку и длиной, например С = 235° - 3,5 мили. Но для определения К_с используют только длины невязок С, независимо от их направления.

Если все используемые обсервации равноточны, то

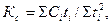
где невязки С_i и соответствующие им интервалы времени t_i счисления между обсервациями.

При расчетах приложения к "Стандартам точности судовождения" ИМО в качестве обобщенных средних для относительных лагов принято при t £ 2 ч К_с = 0.3 – 0.4 мили/час; для абсолютных лагов в два раза меньше.

Погрешности счисления нарастают со временем и поэтому для обеспечения безопасности плавания счисление нуждается в контроле и коррекции по обсервациям.