Оценка точности места судна.
Как следует из определения навигационной изолинии, при перемещении вдоль нее навигационный параметр остается постоянным, а при любом ином перемещении – изменяется. Общее суждение об изменении навигационного параметра в зависимости от перемещения точки дает сетка его изолиний. Так, очевидно, что параметр изменяется наиболее быстро при переходе с одной изолинии на другую по кратчайшему расстоянию между ними, которое при малых расстояниях практически совпадает с нормалью к изолинии. Если Dр – кратчайшее расстояние между смежными изолиниями, то отношение DU/Dр характеризует наибольшую скорость изменения параметра U в данном месте:
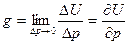 .
.
Градиентом навигационного параметра называется вектор g, направленный по нормали к навигационной изолинии в сторону ее смещения при положительном приращении параметра, модуль этого вектора характеризует наибольшую скорость изменения параметра в данном месте.
Градиент больше в тех местах, где гуще проходят навигационные изолинии, как это показано для трех точек А, В и С на рис. 1.28.
Из формулы (g) и определения градиента навигационного параметра следует, что размерность равна размерности параметра U, поделенной на линейную величину.

Рис. 1.28.
Для определения градиентов вместо точного равенства пользуются приближенным
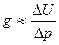 ,
,
где DU – малое приращение навигационного параметра,
Dр - смещение навигационной изолинии.
Расстояние D. Приращение расстояния DD (рис. 1.29.) обусловливает такое же смещение Dр изолинии и поэтому модуль градиента расстояния gD = 1. Направлен этот градиент от ориентира, т.е. t = П +180°. (С - судно, А – мыс).
Высота светила h. Приращение высоты Dh вызывает такое же уменьшение зенитного расстояния Z, которое равно расстоянию до полюса освещения. Поэтому модуль градиента высоты светила такой же, как и расстояния: gh = 1, а направлен градиент к светилу, т.е. t = А, где А – азимут светила.
Пеленг П и обратный пеленг П¢ рассмотрим вначале для небольших удалений от ориентира А, когда участок Земли можно считать плоским (рис.1.29).
Приращение DП пеленга П обусловливает поворот линии пеленга (на рис. 1.29 повернутая линия показана пунктиром) и линейное смещение любой ее точки на величину Dр = DП x D, где DП – в радианах, а D – расстояние до ориентира. Отсюда, выражая DП в градусах, получаем по формуле модуль градиента пеленга:
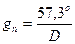 ,
,
 |
Рис. 1.29.
Как видим из рис. 1.29, направление этого градиента t = П - 90°.
Приращение DП обратного пеленга П¢ обусловливает такой же поворот линии пеленга и поэтому градиент для этого случая тот же, что и для пеленга. Направление градиента может быть выражено через обратный пеленг: t = П¢ + 90°.
Обсервованным навигационным параметром (Uo) называется его значение, полученное в результате измерения и исправления всеми необходимыми поправками.
Хорошо известно, что никакие измерения не могут быть абсолютно точными. Поэтому обсервованный навигационный параметр не является "истинным".
Погрешности измерений по характеру их проявления подразделяют на случайные, систематические и промахи.
Случайными называют погрешности, образующиеся от совместного действия многочисленных причин, прямо или косвенно влияющих на результаты измерений. Каждая из этих причин порождает элементарную погрешность, ни одна из которых не превалирует над другими. Выступая в случайных сочетаниях, компенсируя друг друга и складываясь, элементарные погрешности образуют случайные погрешности измерений. Случайные погрешности принимают в отдельных измерениях значения, предсказать или предвычислить которые принципиально невозможно. Такие погрешности подчиняются массовым статистическим закономерностям. В частности, случайные погрешности измерений обычно подчиняются закону нормального распределения вероятностей (закону Гаусса).
В качестве основной характеристики точности в судовождении принято среднее квадратическое отклонение, которое обозначается m с индексом, указывающим на величину, точность которой характеризуется.
Величину m нельзя использовать как поправку для улучшения или исправления результатов измерений, так как она показывает лишь диапазон, в котором с той или иной вероятностью заключены значения (реализации) случайных погрешностей, остающиеся неизвестными. Так, при нормальном распределении погрешности не выходят за пределы ±m с вероятностью 0,683, или 68,3%. Вероятность того, что погрешности не превышают по абсолютной величине удвоенное среднее квадратическое отклонение, т.е. заключены в интервале ±2m, составляет 95,4%. Заметим, что в технике чаще используют близкую к этому 95%-ную погрешность, равную 1,96 m. Наконец, вероятность погрешностей, не выходящих из интервала ±3m равна 99,7%. Так как вероятность выхода за этот интервал, равная 0,3% (т.е. в среднем три случая на тысячу), считается практически пренебрежимо малой, то величину 3m обычно принимают в судовождении предельной погрешностью Dпред. Если обнаруживаются погрешности с абсолютной величиной более 3m, то их относят к грубым погрешностям (промахам). Такие погрешности возникают из-за недостаточной внимательности или квалификации наблюдателя. Измерения с грубой погрешностью расценивают как бракованные, их стремятся выявить и отбросить.
Величина m характеризует рассеивание результатов измерений. Оценка m является статистической характеристикой; она не может быть определена из одиночного измерения, а выводится из серии измерений, выполненных в одинаковых условиях. Если измеряют величину, которая изменяется, то полученные результаты должны быть вначале приведены к одному значению этой величины по скорости ее изменения. Например, при измерении серии высот светила на ходу судна отсчеты секстана приводят к одному моменту и к одному месту (зениту).
По результатам n измерений xi (i = 1, 2,…, n) оценка среднего квадратического отклонения m может быть получена по формуле Бесселя
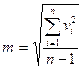 ,
,
где vi = xi – xср – отклонения результатов измерений хi от их среднего хср, при
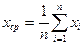 .
.
Систематическими называют постоянные или медленно изменяющиеся погрешности, а также зависящие известным образом от доступных контролю величин. Этими свойствами таких погрешностей пользуются для их уменьшения введением поправок.
Определение поправок всегда сопровождается появлением случайных погрешностей, которые, однако, проявляются затем систематически или случайно в зависимости от решаемой задачи. Остаточные погрешности (после введения поправок) оценивают, как и случайные, средней квадратической величиной.
Полной, суммарной или результирующей называют погрешность, имеющую случайную и систематическую составляющие, как и бывает обычно на практике. Обозначая среднюю квадратическую величину полной погрешности mn, а названных ее составляющих mсл и mсист, по правилу сложения дисперсий имеем при одиночном измерении
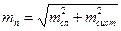 ,
,
а при осреднении n измерений уменьшается только случайная составляющая:
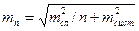 .
.
Если измеряют однородные навигационные параметры с общей для них систематической погрешностью, то она обуславливает взаимную зависимость между полными погрешностями. Эта зависимость статистическая ("в среднем") и характеризуется коэффициентом корреляции r, который при равноточных измерениях выражается формулой
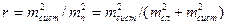
Всегда ½r½ £ 1. Если r = 0, то погрешности независимы, а при ½r½ = 1 между ними однозначная линейная зависимость.
Для получения надежных оценок требуются большие серии измерений. При определениях места это невозможно и поэтому в практике судовождения основными являются априорные характеристики точности.
Априорные (от лат. a priori – до опыта) характеристики точности обобщают результаты специальных исследований и опыт таких же измерений в сходных условиях.
Таблица 3
Априорные значения средних квадратических погрешностей
m измерений навигационных параметров
| Измеряемый навигационный параметр | m | Примечания |
| Пеленг по магнитному компасу | 0,5-1,5° | |
| Гирокомпасный пеленг | 0,3-0,5° | |
| Радиопеленг: Днем Ночью | 1,0-1,5° 2,0-3,0° | |
| Радиолокационный пеленг | 1,0-1,5° | |
| Радиолокац. Расстояние | 1% от D 0,6% от D | На шкалах до 4 миль На других шкалах |
| Горизонтальный угол | 1-2¢ | |
| Высота светила | 0,5-1,5¢ | |
| Параметр РНС "Лоран-С" Поверхностный Пространственный | 0,2-0,5 мкс 1-2 мкс | Автоматический Приемоиндикатор |
Приращение навигационного параметра DU вызывает смещение линии положения Dр, зависящее от градиента:
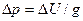 ,
,
Переходя в этом равенстве к средним квадратическим погрешностям, получаем важную формулу
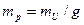 ,
,
которая выражает среднюю квадратическую погрешность линии положения mр в зависимости от такой же погрешности навигационного параметра mU.
Если обсервованное значение навигационного параметра Uo изменить в обе стороны на его среднюю квадратическую погрешность mU, то соответствующие этому смещение изолинии (штриховые на рис. 1.30.) укажут границы средней квадратической полосы положения.

Рис. 1.30.
Вероятность нахождения места внутри средней квадратической полосы при нормальном распределении равна 68,3%. Расширение полосы увеличивает такую вероятность. Утроенную полосу называют предельной полосой положения - ей соответствует вероятность нахождения места 0,997, или 99,7%.
Вследствие неизбежных погрешностей измерений навигационных параметров обсервованное место судна не совпадает с истинным. Погрешность места, как и порождающие ее погрешности измерений параметров, носит случайный характер.
Оценивание точности определений места должно основываться на массовом статистическом исследовании погрешностей измерений, от которых зависит точность обсерваций. Любая оценка точности говорит лишь о вероятности нахождения действительного места судна в пределах определенной области. Практически такие оценки оправдываются только в среднем для многих обсерваций.
При анализе точности обсерваций принимают, что истинное место судна хотя и неизвестно, но оно не случайно, оно есть, но не известно в какой точке.
Наиболее полную характеристику точности места дает эллипс погрешностей с центром в обсервованной точке.
Если для расчетов или построения эллипса используют средние квадратические погрешности линий положения, то получают средний квадратический эллипс. Вероятность нахождения в нем места при нормальном распределении составляет только 39,3%. Этот эллипс (его оси) надо увеличить в 2,5 раза чтобы получить принятую "Стандартами точности судовождения" ИМО 95%-ную фигуру погрешностей. Вместо этого проще сначала увеличить в 2,5 раза средние квадратические погрешности линий положения, используя которые сразу получают 95%-ный эллипс погрешностей места.
Любой эллипс задается тремя параметрами, например, полуосями и углом ориентации одной из них. Формулы для расчета таких параметров весьма сложны и по ним составлены программы для судовых ЭВМ. При решении задач вручную ограничиваются построением эллипсов по двум изолиниям или линиям положения (рис. 1.31).

Рис. 1.31.
1) пользуясь априорными оценками точности измерений найти полные средние квадратические погрешности mп обоих параметров и увеличить их в 2,5 раза;
2) построить две 95%-ные полосы положения;
3) в образовавшийся пересечением этих полос четырехугольник погрешностей вписать на глаз от руки эллипс и оценить параметры.
В большинстве случаев эллипс погрешностей места имеет форму, близкую к окружности. Этим пользуются для оценки точности места одним числом М – средней квадратической погрешностью места. Величину М принимают радиусом круга с центром в оцениваемой точке и называют также круговой погрешностью места.
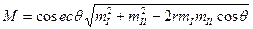 ,
,
где mI и mII - полные средние квадратические погрешности линий положения с
коэффициентом корреляции r между ними;
q - угол между градиентами.
Заменяя здесь mI и mII по формуле (mp), получаем общую формулу средней квадратической погрешности места:
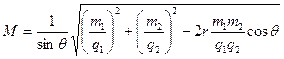 ,
,
где m1 и m2 - средние квадратические погрешности навигационных параметров, градиенты которых g1 и g2.
Подставляя в общую формулу выражения градиентов разных навигационных параметров, получают формулы для расчета М при разных способах определений, что будет делаться далее. При обсервациях по параметрам, полные погрешности которых независимы, (r = 0) формула упрощается:
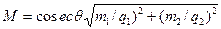 ,
,
где q - угол между ЛП.
Круговая погрешность М связана с полуосями среднего квадратического эллипса погрешностей a и b следующим равенством
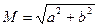 .
.
Видим, что круг радиуса М всегда охватывает такой эллипс (рис. 1.32), вероятность нахождения в котором при нормальном распределении всегда 39,3%, а внутри круга – зависит от сжатия эллипса и изменяется от 63 до 68% (ориентировочно принимают ~ 65%).

Рис. 1.32.
Чтобы получить радиус круга, внутри которого место находится с вероятностью 95%, как предусмотрено стандартами ИМО, надо умножить М на коэффициент ~ 1,9. Поэтому с некоторым «Запасом» можно принимать радиус R 95%-ного круга погрешностей как удвоенную среднюю квадратическую погрешность места М, т.е.
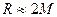 .
.
Этим равенством будем далее пользоваться для оценки точности места в соответствии с требованиями "Стандартов точности судовождения" ИМО.
В стандарте ИМО плавание подразделяется на два вида: 1) акватории портов и подходы к ним, включая все районы, где затруднено маневрирование судна; 2) другие районы. Граница между этими видами плавания четко не определяется и зависит от конкретных условий (Резолюция А815(1995 г.).
При плавании в стесненных водах точность £10 м. При плавании в других районах со скоростью до 30 уз. текущее место судна должно быть известно с погрешностью не более 4% расстояния до ближайшей опасности, но не более 4 миль. При этом точность места должна оцениваться вероятностью 95%-ной фигурой погрешностей с учетом случайных и систематических погрешностей.
Дата добавления: 2016-08-06; просмотров: 4671;











