Аналитическое отделение корней

Аналитическое отделениекорней основано на следующей теореме.

Если функцияf(x) непрерывна и монотонна на отрезке[a;b]и принимает на концах отрезка значения разных знаков, то на отрезке [a;b] содержится один корень уравнения f(x)=0.

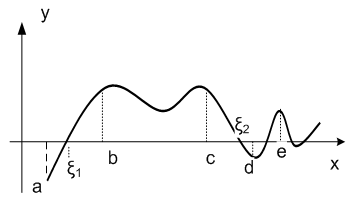
Действительно, если условия теоремы выполнены, как это имеет место на отрезке [a;b] (рис. 1.2.2-3), то есть f(a)∙f(b)<0 и f'(x)>0 для xÎ [a;b], то график функции пересекает ось 0Х только один раз и, следовательно, на отрезке [a;b] имеется один корень 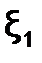уравнения f(x) =0.

Аналогично можно доказать единственность корня 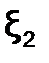на отрезке [c;d], 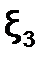на[d;e]и т.д

Рис. 1.2.2-3

Таким образом, для отделения корней нелинейного уравнения необходимо найти отрезки, в пределах которых функция монотонна и изменяет свой знак. Принимая во внимание, что непрерывная функция монотонна в интервалах между критическими точками, при аналитическом отделении корней уравнения можно рекомендовать следующий порядок действий:

1)установить область определения функции;

2)определить критические точки функции, решив уравнение f¢(x)=0;

3)составить таблицу знаков функции f(x) в критических точках и на границах области определения;

4)определить интервалы, на концах которых функция принимает значения разных знаков.

Пример 1.2.2-3.Отделить корни уравнения x - ln(x+2) = 0.

Область допустимых значений функции f(x) = x - ln(x+2) лежит в интервале (-2; ∞), найденных из условия x+2>0. Приравняв производную f¢(x)=1-1/(x+2)к нулю, найдем критическую точкух_k= -1. Этиданные сведены в табл.1.2.2-1 и табл. 1.2.2-2 знаков функции f(x).

Таблица1.2.2-1 Таблица 1.2.2-.2

Уравнение x - ln(x+2) = 0 имеет два корня 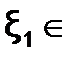(-2;-1] и 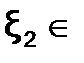[-1; ∞) . Проверка знака функции внутри каждого из полученных полуинтервалов (табл.1.2.2) позволяет отделить корни уравнения на достаточно узких отрезках 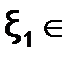[-1.9;-1.1] и 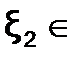[-0.9;2.0].

Уточнение корней

Задача уточнения корня уравнения 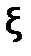с точностью 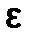, отделенного на отрезке [a;b], состоит в нахождении такого приближенного значения корня 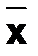, для которого справедливо неравенство 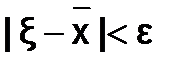.Если уравнение имеет не один, а несколько корней, то этап уточнения проводится для каждого отделенного корня.