Географические координаты и их разности

Основной в навигации принята географическая система координат, которую составляют широта и долгота.

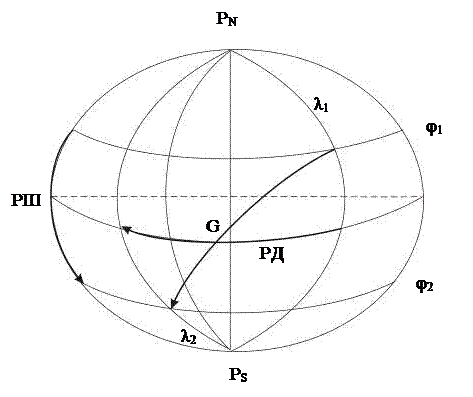
Широтой j называют угол между плоскостью экватора и нормалью к эллипсоиду в данной точке (дуга меридиана от экватора до данной параллели, см. рис. 1.1.). Широта измеряется от экватора (0°) к полюсам (90°), ей приписывают наименования норд N или зюйд S, а в расчетах – знаки + или -.

Долготой l называют двугранный угол между плоскостями гринвичского меридиана (G на рис. 1.1.) и меридиана места. Меридиан Гринвичской обсерватории близ Лондона принят за начальный международным соглашением 1884 г. Долгота измеряется дугой экватора от гринвичского меридиана в обе стороны до 180° и ей приписывают наименования ост Е или вест W, а в расчетах – знаки + или -.

В навигации j и l выражают в градусах и минутах с десятыми (если надо, то и с сотыми) долями минуты, а при расчетах на калькуляторах – в градусах с десятичными долями. Всегда первой записывают широту.

При переходе от одной точки к другой в общем случае изменяются обе координаты. Эти изменения выражают как разность широт РШ и разность долгот РД (меньшие дуги соответственно меридиана и экватора, от 0° до 180°), им приписывают наименования или знаки: к N (+), к S (-) и к Е (+), к W (-). Так, если судно переместилось между точками 1 и 2, что отмечено индексами у их координат, то

; .

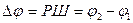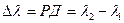Отсюда видно, что при известных координатах первой точки, а также РШ и РД обусловленные перемещением судна, то координаты второй точки

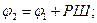
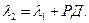
Эти формулы применяются в аналитическом счислении и при расчетах обсервованных координат места судна.

Пример: j₁ = 50°N, l₁ = 40°Е;

j₂ = 20°S, l₂ = 25°W;

РШ = -20° - 50° = -70° (к S)

РД = -25° - 40° = -65° (к W)

Рис. 1.2.

Для расчетов и построений на эллипсоиде необходимо знать кривизну его поверхности в каждой точке. Такая кривизна вполне описывается двумя главными радиусами кривизны. Эти радиусы получаются в сечениях эллипсоида нормальными (вертикальными) и взаимоперпендикулярными плоскостями: меридиана М и первого вертикала N. Радиус кривизны М меридианного эллипса выражается формулой:

,

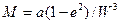где .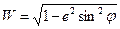

Радиус кривизны N эллипса от сечения эллипсоида плоскостью первого вертикала:

.

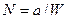Радиус r параллели в широте j:

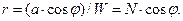
Заметим, что при j = 90° 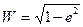, и М = N. При любой другой широте М < N; на полюсе М больше, чем на экваторе.

Полученные формулы главных радиусов кривизны эллипсоида используются в дальнейшем.