Выравнивание по прямой ряда динамики урожайности

Ряды динамики

Часто уровни динамического ряда не отражают четко выраженной тенденции. В этом случае ее выявляют с помощью особых приемов обработки динамических рядов.

Одним из наиболее простых способов изучения общей тенденции в ряду динамики являетсяукрупнение интервалов. При данном методе вместо первоначальных уровней рассматривают укрупненные периоды, характеризуя их либо средними, либо абсолютными величинами.

Вторым методом является сглаживание динамического ряда на основе скользящей средней.Данный метод позволяет построить новый ряд, в котором число уровней сократится. Порядок расчета новых уровней (временной интервал сглаживания - 3 года) следующий:

; ; .

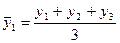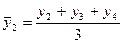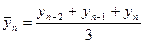Более совершенным приемом изучения общей тенденции в рядах динамики является аналитическое выравнивание. Смысл его заключается в том, что изменения уровней ряда динамики могут быть с той или иной степенью приближения выражены определенными математическими функциями, т.е. выравнивание динамического ряда:

по уравнению прямой 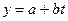(I)

по уравнению гиперболы 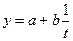(II)

по уравнению параболы второго порядка 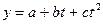(III) ,

где a , b и с - параметры уравнения, которые следует найти

t - период времени.

Решение данных уравнений производится при помощи системы уравнений:

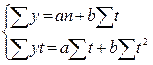I II

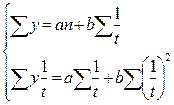
III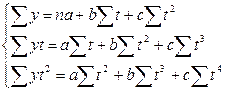

Рассмотрим на примере урожайности зерновых культур выравнивание ряда динамики по прямой.

Выравнивание по прямой ряда динамики урожайности

Зерновых культур

Годы	Фактическая урожайность, ц/га y	Расчетные данные
t		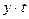t2	выравненный уровень урожайности, ц/га
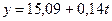
	15,4 14,0 17,6 15,5 13,7 17,5 14,8 18,5 15,1		15,4 28,0 52,8 62,0 68,5 105,0 103,6 148,0 135,9		15,23 15,37 15,51 15,65 15,79 15,93 16,07 16,21 16,35
Σ	142,1		719,2		142,1

Для определения параметровa и b подставим в систему приведенных выше уравнений (I) суммы признаков Σy и Σt, сумму их произведений Σyt и сумму квадратов номеров лет Σt² (см. расчетные данные табл.4.2):

142,1=9a+45b

719,2=45a+285b

Выравняем коэффициенты при a, разделив первое уравнение на число лет n= 9, а второе на Σt =45:

15,79=a+5,0b

15,98=a+6,33b

Вычтем из второго уравнения первое и определим значение b: 0,19=1,33b, отсюда b=0,14.

Подставим b=0,14 в одно из уравнений и рассчитаем значение a: 15,79=a+5,0·0,14; a=15,09.

Таким образом, уравнение для выравнивания динамического ряда имеет вид: 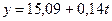. Такое уравнение называют трендом. Значение коэффициента b в данном уравнении показывает, что несмотря на значительные колебания в отдельные годы, наблюдается тенденция увеличения урожайности: с 1994 по 2002 гг. урожайность зерновых культур в среднем возрастала на 0,14 ц/га.

Выравненные (сглаженные) уровни получают, подставляя в уравнение номера лет t. Для 1994 г. при t=1 выравненный уровень составит 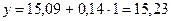ц/га, для 1995 г. при t=2 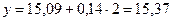ц/га и т. д. (см. табл. 4.2).

Фактические и выравненные уровни урожайности зерновых культур представлены в виде графика.

Рис. Урожайность зерновых культур, ц/га

Соединив точки, построенные по фактическим данным, получим ломанную линию, на основании которой затруднительно вынести суждение о характере общей тенденции в изменении урожайности.

Тенденция роста урожайности зерновых культур в изучаемом периоде отчетливо проявляется в результате построения выравненной прямой

.

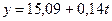Для оценки степени приближения выравненных уровней к фактическим определяют среднее отклонение:

,

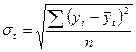где 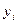- фактические уровни динамического ряда

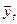- уровни, вычисленные по уравнению

n - число периодов (уровней).

Данный показатель является абсолютным показателем случайной колеблемости уровней динамического ряда. Если его отнести к среднему уровню ряда ( 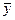) и выразить это в процентах, то получим относительный показатель колеблемости, который применяют для сравнения степени колеблемости разных динамических рядов.

Кроме вышеперечисленных методов выранивание динамических рядов производят по среднему абсолютному приросту и среднему коэффициенту роста по следующим формулам:

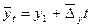и ,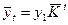

где t - порядковый номер ряда.

Для исходного уровня t = 0 , далее значения t берутся за 1,2…….и т.д.

Эстраполяция. Под экстраполяцией понимают нахождение уровней за пределами изучаемого ряда, то есть продление в будущее тенденции, наблюдавщейся в прошлом. Поскольку в действительности тенденция развития не остается неизменной, то данные, получаемые путем экстраполяции ряда, следует рассматривать как вероятностные оценки.

Экстраполяцию рядов динамики осуществляют различными способами , например, экстраполируют ряды динамики выравниванием по аналитическим формулам. Зная уравнение для теоретических уровней и подставляя в него значения t за пределами исследованного ряда, рассчитывают для t вероятностные уровни (у_t).