Экономические приложения производной.

Эластичность функции.

Предельный анализ

Производные применяются в экономике для получения так называемых предельных издержек, предельной выручки, предельной прибыли и т. п.Слово «предельный» означает производную или скорость изменения.Если функция 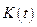выражает количество произведенной однородной продукции K за время t, то 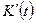— производительность труда в момент t (предельная производительность). Если функция 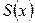выражает издержки производства однородной продукции в количестве х, то 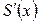выражает предельные издержки производства (характеризирует приближенно дополнительные затраты на производство единицы дополнительной продукции). Если 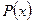прибыль от продажи х единиц товара то 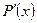предельная прибыль. Одним из основных законов теории производства утверждает: Оптимальный для производства Уровень выпуска товара определяется равенством граничных затрат и предельного дохода.

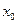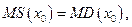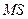То есть уровень выпуска является оптимальным, для производства, если где — предельные затраты; 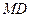— предельный доход. Это следует из того, что прибыль 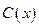равна 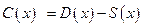. Максимальная прибыль будет при 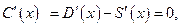то есть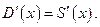

Средние издержки 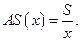Минимум этой величины достигается в точк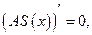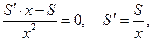е т. е.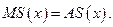

Функция потребления и сбережения. Доход у населения разбивается на две части: одну часть 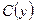(функция потребления) оно тратит на потребление, а другую 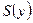(функция сбережения) оставляет на сбережения. Очевидно, что 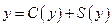и

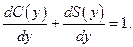
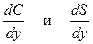— предельные склонности к потреблению и сбережению.

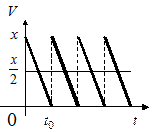Издержки хранения. Совокупные издержки производства товара состоят из издержек его производства и издержек хранения.Пусть товар завозится на склад партиями по х штук в партии, а расходуется с постоянной скоростью.

Тогда наполняемость склада зависит от времени t и задается функцией, график которой изображен на чертеже. Здесь V —число единиц товара на складе, 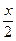— средняя наполняем ость склада, 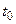— время использования партии.

Эластичность. Эластичность (относительная производная) функции показывает приближенно, на сколько процентов изменится функция 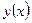при изменении независимой переменной х на1%. Эластичность функции 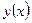определяется по формуле .

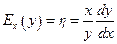Для упрощения процесса дифференцирования (особенно произведения степенных функций) иногда используется логарифмическая производная .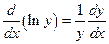

В терминах логарифмических производных .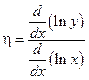

Если известна функция спроса 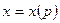, можно предельную выручку по отношению к цене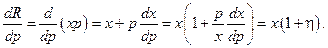

Если y — спрос, x — цена, то при:

1) 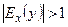— спрос считают эластичным,

2) 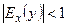— неэластичным,

3) 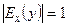— с единичной эластичностью.

Есть другие определения эластичности.

Имеют место формулы:

.

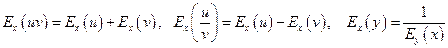Пример 4.25. Зависимость между себестоимостью единицы продукции y(тыс.грн.) и выпуском продукции (тыс.грн.) выражается функцией 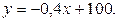Найти эластичность себестоимости при выпуске продукции на 50 тыс. грн.

Решение. Определяем эластичность

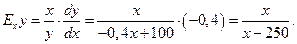
При 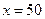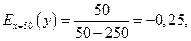т. е. при выпуске продукции на 50тыс. грн. Увеличение ее на 1%приведет к снижению себестоимости на 0,25%.

Пример 4.26.Производственная функция имеет вид 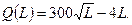, где L – численность работающих, Q(L)- объем производства.

Найти предельную производительность труда. Провести анализ.

Решение. Предельная производительность труда равна

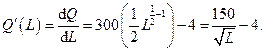
Вычислим предельную производительность при разной численности рабочих L.

L						1406,25
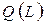
									-748490
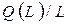
					4,0	4,	3,9		-3,364
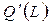
					0,0		-0,0	-1	-3,6

Из таблицы видно что предельная производительность труда уменьшается с ростом числа рабочих и начиная с 1407 становится отрицательной. Такая ситуация часто наблюдается на практике. Аналитически это означает что производственные функции, как правило, вогнутые, т. е. .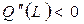

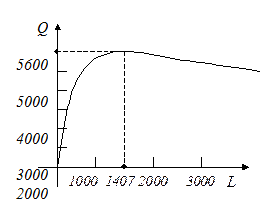
Наконец, дадим еще раз, экономический смысл первой, второй и третьей производной на примере производительности труда.

Таким образом, производственная функция возрастающая 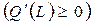и вогнутая 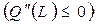. График нашей функции имеет вид, изображенный на рисунке. То, что функция стала убывать значит, что область ее определения отрезок, лежащий между 0 и1407.

Количество персонала L
Количество продукции.
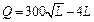
908,6833	950,9874	991,2305	1029,665	1066,497	1101,895	5486,833	5487,575	5488,315
Средняя производительность.
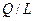
90,86833	86,4534	82,60254	79,20503	76,17837	73,45967	5,486833	5,482093	5,47736
Предельная производительность: Изменение объема выпускаемой продукции при увеличении числа персонала на единицу.
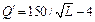
43,43416	41,2267	39,30127	37,60251	36,08919	34,72983	0,743416	0,741047	0,73868
Характер изменения предельной производительности: С ростом числа персонала предельная производительность уменьшается.
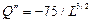
-2,37171	-2,05576	-1,80422	-1,6001	-1,43176	-1,29099	-0,00237	-0,00237		-0,00236
Темп изменения предельной производительности: С ростом числа персонала предельная производительность уменьшается с уменьшающимся темпом.
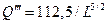
0,355756	0,280331	0,225527	0,184627	0,153402	0,129099	3,56E-06	3,55E-06	3,54E-06

Обратите внимание на то, как связаны между собой строки.

Например .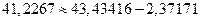

Понятие вогнутости функции находит свою интерпретацию в экономической теории. Одним из основных экономических законов — закон убывающей доходности, который формулируется так: с ростом производства дополнительная продукция, полученная на каждую новую единицу ресурса (трудового, технологического и других) с некоторого момента убывает. Этот закон означает, что функция 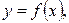которая выражает зависимость выпуска продукции от вложенных ресурсов, есть функция вогнутая.

Другим важным понятием экономической теории является функция полезности 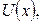где х — товар; U — полезность. Эта функция дает субъективную оценку товара для каждого отдельного потребителя, но достаточно объективную оценку для общества в целом. Закон убывающей полезности такой: с ростом количества товара, дополнительная полезность каждой новой единицы продукции с некоторого момента бывает. Это означает, что функция полезности вогнута.

Пример 4.27. Эпидемия медленно распространяется среди населения. Число заболевших определяется формулой 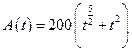, где t — число недель, прошедших с момента начала эпидемии. Найти скорость изменения числа заболевших в момент времени: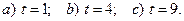

ЛИТЕРАТУРА