Нормований середній бал

Нормований середній бал застосовується для ознак рангової шкали.

Рангова шкала визначає не тільки подібність елементів, а і послідовність типу "більше-менше", "краще, ніж" тощо.

Для розрахунку нормованого середнього балу необхідно, спочатку, ранжувати значення ознаки в порядку зростання якості. Тоді:

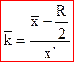де 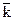- нормований середній бал;

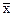- середньозважений ранг;

R – різниця між максимальним і мінімальним значенням рангу.

x' – середина шкали рангів.

Приклад №3. Обстеження показало відношення населення району до медичного обслуговування:

повністю задоволені 15%

частково 50%

не задоволені 35%.

Яке ж в середньому ставлення населення до медичного обслуговування?

Проведемо ранжування: найкраще відношення – 3 бали, частково – 2 бали, не задоволені – 1 бал.

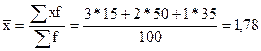
R = x_max – x_min = 3 – 1 = 2

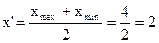
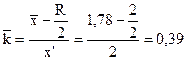
Отже, 39% населення оцінюють медичне обслуговування як задовільне (оскільки за найвищий ранг ми взяли найкраще обслуговування)[8].

Таким чином, середня величина є узагальнюючою мірою ознаки, що варіює, у статистичній сукупності. Показник у формі середньої характеризує рівень ознаки в розрахунку на одиницю сукупності. Як уже зазначалося, значення ознаки j-го елемента поєднує в собі як спільні для всієї сукупності типові риси, так і притаманні лише цьому елементу індивідуальні особливості. Абстрагуючись від індивідуальних особливостей окремих елементів, можна виявити те загальне, типове, що властиве всій сукупності.

Саме в середній взаємно компенсуються індивідуальні відмінності елементів та узагальнюються типові риси. Типовість середньої пов’язана з однорідністю сукупності. Середня характеризуватиме типовий рівень лише за умови, що сукупність якісно однорідна. У неоднорідній сукупності, за влучним висловом П. Самуельсона, осереднюються «тигри та кицьки», що лише створює ілюзію «благоденствія» і не віддзеркалює реалій.

Взаємозв’язок індивідуальних значень ознаки та середньої — це діалектична єдність загального і окремого. Замінюючи множину індивідуальних значень, середня не змінює визначальної властивості сукупності — загального обсягу явища. Зв’язок визначальної властивості з елементами сукупності описується функцією f (x₁, x₂, ... x_n), яка виражає певну математичну дію над емпіричними значеннями ознаки (підсумовування, множення, степенювання, коренювання) і визначає вид середньої. Так, у разі підсумовування значень ознаки визначальну властивість забезпечує середня арифметична, при множенні — середня геометрична і т. д.

Отже, при обчиᑁленні середніх у соціально-економічних дослідженнях необхідно чітко усвідомити визначальну властивість сукупності та логіко-математичну суть — логічну формулу — показника. Наприклад, логічна формула середнього вкладу в банк:

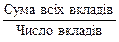Чисельник логічної формули середньої являє собою обсяг значень (визначальну властивість) ознаки, що варіює, а знаменник — обсяг сукупності. Як правило, визначальна властивість — це реальна абсолютна чи відносна величина, яка має самостійне значення в аналізі. У кожному конкретному випадку для реалізації логічної формули використовується певний вид середньої, зокрема:

а) середня арифметична;

б) середня гармонічна;

в) середня геометрична;

г) середня квадратична і т. д.

Залежно від характеру первинної інформації середня будь-якого виду може бути простою чи зваженою. Позначається середня символом 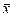(риска над символом означає осереднення індивідуальних значень) і вимірюється в тих самих одиницях, що й ознака.