Середня арифметична

Оскільки для більшості соціально-економічних явищ характерна адитивність обсягів (виробництво цукру, витрати палива тощо), то найпоширенішою є арифметична середня, яка обчислюється діленням загального обсягу значень ознаки на обсяг сукупності. За первинними, незгрупованими даними обчислюєть­ся середня арифметична проста:

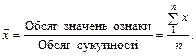
Наприклад, за місяць страхова компанія виплатила страхове відшкодування за п’ять ушкоджених об’єктів на суму, тис. грн.: 18, 27, 22, 30, 23. Середня сума виплати страхового відшкодування, тис. грн.:

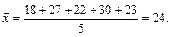
За формулою простої арифметичної обчислюються середні у динамічному ряду. Якщо в січні агрофірма продала молокозаводу 315, у лютому — 305, а в березні — 340 т молока, то середньомісячний продаж молока, т: (315 + 305 + 340) : 3 = 320.

Моментні показники замінюються середніми як півсума значень на початок і кінець періоду. Якщо моментів більш ніж два, а інтервали часу між ними рівні, то в чисельнику до півсуми крайніх значень додають усі проміжні, а знаменником є число інтервалів, яке на одиницю менше від числа значень ознаки. Таку формулу називають середньою хронологічною:

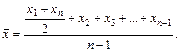
Наприклад, на фірмі залишки обігових коштів на початок кожного місяця І кварталу становили, млн грн.: січень — 70, лютий — 82, березень — 77, квітень — 80. Середньомісячний залишок обігових коштів, млн грн.:

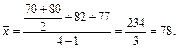
У великих за обсягом сукупностях окремі значення ознаки (варіанти) можуть повторюватись. У такому разі їх можна об’єднати в групи (j = 1, 2, ..., m), а обсяг значень ознаки визначити як суму добутків варіант х_j на відповідні їм частоти f_j, тобто як 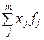. Такий процес множення у статистиці називають зважуванням, а число елементів сукупності з однаковими варіантами — вагами. Сама назва «ваги» відбиває факт різновагомості окремих варіант. Значення ознаки осереднюються за формулою середньої арифметичної зваженої:

Вагами можуть бути частоти або частки (відносні величини структури), іноді інші величини (абсолютні показники). Припустимо, у фірмі працює 20 налагоджувачів аудіо- та відеоапаратури, з них три мають 4-й розряд, дев’ять — 5-й, вісім — 6-й. Середній тарифний розряд

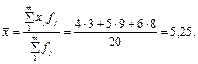
Середня не збігається з жодним значенням ознаки, але це типовий рівень кваліфікації налагоджувачів фірми.

Формально між середньою арифметичною простою і середньою арифметичною зваженою немає принципових відмінностей. Адже багаторазове (f раз) підсумовування значень однієї варіанти замінюється множенням варіант х на вагу f. Проте функціонально середня зважена більш навантажена, оскільки враховує поширеність, повторюваність кожної варіанти і певною мірою відображує склад сукупності. Значення середньої зваженої залежить не лише від значень варіант, а й від структури сукупності. Чим більшу вагу мають малі значення ознаки, тим менша середня, і навпаки. Наприклад, незважаючи на той факт, що в двох регіонах мешкають люди різного віку, у тому регіоні, де більше дітей, середній вік населення буде менший. На цю властивість середніх слід зважати при використанні їх у порівняльному аналізі сукупностей, склад яких істотно різний. У таких випадках, аби елімінувати (усунути) вплив структури сукупності на середню, вдаються до пошуку стандартизованих ваг.

У структурованій сукупності при розрахунку середньої зваженої варіантами можуть бути як окремі значення ознаки, так і групові середні 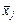, кожна з яких має відповідну вагу у вигляді групових частот f_j:

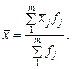
Обчислену так середню на відміну від групових називають загальною.

Як приклад використаємо групові середні альтернативної ознаки, яка набуває взаємовиключних значень 1 або 0. Відповідні цим значенням частоти f₁ та f₀. Очевидно, середня такої ознаки є часткою d₁:

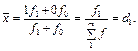
Так, за даними перепису населення в регіоні проживало 5,2 млн осіб, із них у містах — 3,5, у сільській місцевості — 1,7. Частка осіб працездатного віку відповідно становила 0,60 та 0,48.

Середня частка населення працездатного віку в регіоні є арифметичною зваженою з групових часток:

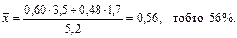
Середня арифметична має певні властивості, які розкривають її суть.

1. Алгебраїчна сума відхилень окремих варіант ознаки від середньої дорівнює нулю:

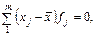
тобто в середній взаємно компенсуються додатні та від’ємні відхилення окремих варіант.

2. Сума квадратів відхилень окремих варіант ознаки від серед­ньої менша, ніж від будь-якої іншої величини:

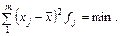
3. Якщо всі варіанти збільшити (зменшити) на одну й ту саму величину А або в А раз, то й середня зміниться аналогічно.

Ця властивість найвиразніше ілюструється на прикладі ознак порядкової (рангової) шкали, для якої використовуються різні варіанти оцифрування. Так, окремим пунктам 3-бальної шкали можна надати значень 1, 2, 3 або –1, 0, 1. Очевидно, розраховані для цих варіант оцифрування середньозважений 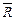та середній центрований 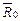бали відрізнятимуться на величину А = 2. Так, за даними табл. 4.2 оцінимо ставлення населення до смертної кари.

Таблиця 4.2