В ЛОКАЛЬНОЙ СИСТЕМЕ КООРДИНАТ
ФЕРМЕННЫЙ КОНЕЧНЫЙ ЭЛЕМЕНТ
 Ферменный КЭ применяется для моделирования прямолинейных стержней конструкции, работающих на растяжение-сжатие (рис. 4.5). Обозначения: 1; 2 - локальные номера узлов КЭ;
Ферменный КЭ применяется для моделирования прямолинейных стержней конструкции, работающих на растяжение-сжатие (рис. 4.5). Обозначения: 1; 2 - локальные номера узлов КЭ; 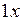 - локальная ось,
- локальная ось, 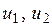 - узловые перемещения КЭ в локальной системе координат. Будем считать, что в пределах КЭ погонная нагрузка
- узловые перемещения КЭ в локальной системе координат. Будем считать, что в пределах КЭ погонная нагрузка 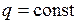 , продольная жесткость
, продольная жесткость 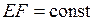 .
.
Представим перемещение 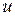 произвольной точки КЭ в виде линейной функции локальной координаты
произвольной точки КЭ в виде линейной функции локальной координаты 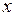 :
: 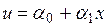 . Постоянные
. Постоянные 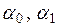 определяются из условий:
определяются из условий: 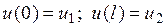 . Это дает систему уравнений
. Это дает систему уравнений 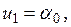
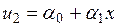 , из которой следует:
, из которой следует: 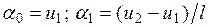 . Подставляя
. Подставляя 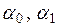 в выражение для
в выражение для 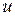 , получаем
, получаем
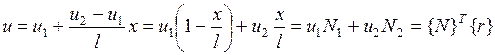 . (4.3.1)
. (4.3.1)
Здесь 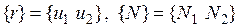 . Функции распределения
. Функции распределения 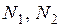 имеют вид:
имеют вид: 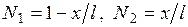 .
.
Перейдем к определению полной потенциальной энергии КЭ.
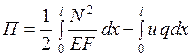 . (4.3.2)
. (4.3.2)
Продольную силу 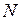 можно связать с перемещением
можно связать с перемещением 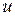 зависимостью
зависимостью
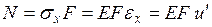 ,
,
с учетом чего выражение (4.3.2) примет вид
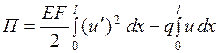 .
.
Для элемента, находящегося в равновесии, справедливо вариационное уравнение Лагранжа
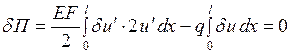 . (4.3.3)
. (4.3.3)
Примем во внимание аппроксимацию (4.3.1): 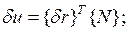
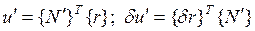 . Подставляя эти выражения в (4.3.3), получаем
. Подставляя эти выражения в (4.3.3), получаем
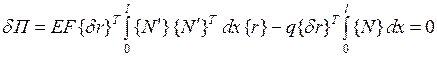 .
.
Отсюда при 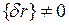 следует матричное уравнение
следует матричное уравнение 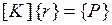 , где
, где 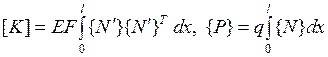 - соответственно матрица жесткости и вектор нагрузки КЭ. Получим окончательные выражения для вычисления
- соответственно матрица жесткости и вектор нагрузки КЭ. Получим окончательные выражения для вычисления 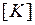 и
и 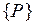 :
:
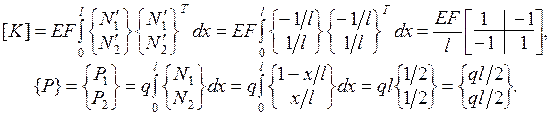
БАЛОЧНЫЙ КОНЕЧНЫЙ ЭЛЕМЕНТ
 Балочный КЭ (рис. 4.6) применяется для моделирования стержней конструкции, находящихся в состоянии поперечного изгиба. Для воспроизведения такого состояния в качестве узловых перемещений КЭ принимаются прогибы
Балочный КЭ (рис. 4.6) применяется для моделирования стержней конструкции, находящихся в состоянии поперечного изгиба. Для воспроизведения такого состояния в качестве узловых перемещений КЭ принимаются прогибы 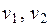 и углы поворота
и углы поворота 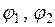 его узлов. Будем считать, что в пределах КЭ погонная нагрузка
его узлов. Будем считать, что в пределах КЭ погонная нагрузка 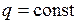 , жесткость на изгиб
, жесткость на изгиб 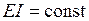 и справедлива гипотеза прямых нормалей, согласно которой
и справедлива гипотеза прямых нормалей, согласно которой 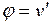 .
.
Представим прогиб 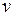 в пределах элемента в виде:
в пределах элемента в виде: 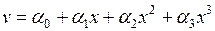 . Постоянные
. Постоянные 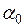 ,
, 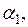
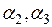 определяются из условий:
определяются из условий:
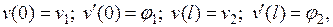
что приводит к системе уравнений
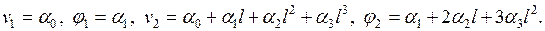
Из этой системы следует:
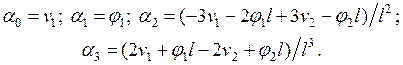
Подставляя 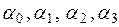 в выражение для
в выражение для 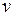 , получаем
, получаем
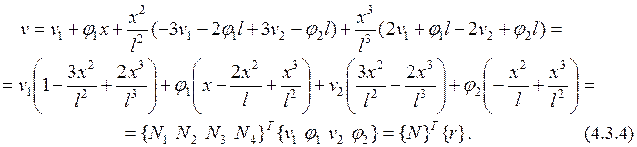
Здесь 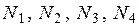 - функции распределения:
- функции распределения:
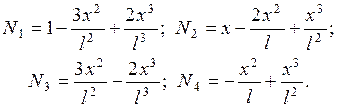
Полная потенциальная энергия балочного КЭ определяется выражением
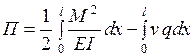 .
.
Изгибающий момент 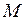 в каждой точке элемента пропорционален кривизне
в каждой точке элемента пропорционален кривизне 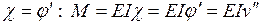 . С учетом этого получаем
. С учетом этого получаем
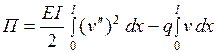 .
.
В состоянии равновесия конечного элемента 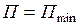 . Необходимое условие этого записывается в виде вариационного уравнения Лагранжа
. Необходимое условие этого записывается в виде вариационного уравнения Лагранжа
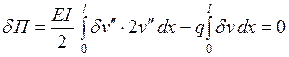 . (4.3.5)
. (4.3.5)
Согласно (4.3.4) имеем: 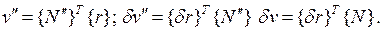 С учетом этого уравнение (4.3.5) принимает вид
С учетом этого уравнение (4.3.5) принимает вид
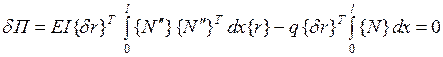 .
.
Отсюда при 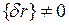 следует матричное уравнение равновесия обобщенных внутренних (в левой части) и внешних (в правой части) узловых сил конечного элемента
следует матричное уравнение равновесия обобщенных внутренних (в левой части) и внешних (в правой части) узловых сил конечного элемента
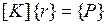 ,
,
где 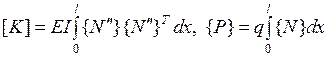 - соответственно матрица жесткости и вектор нагрузки данного элемента.
- соответственно матрица жесткости и вектор нагрузки данного элемента.
Получим выражения для вычисления матрицы 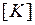 и вектора
и вектора 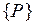 :
:
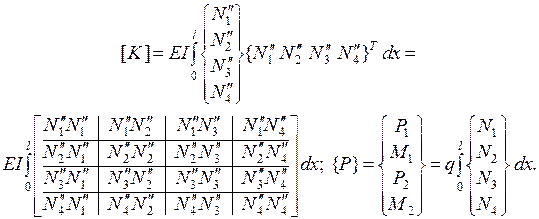
После нахождения определенных интегралов окончательно имеем:
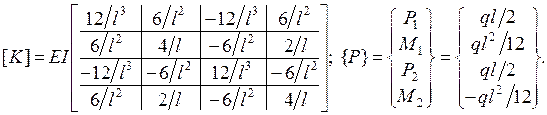
Положительные направления внешних узловых сил 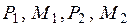 в векторе
в векторе 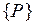 совпадают с положительными направлениями соответствующих узловых перемещений КЭ (рис. 4.6).
совпадают с положительными направлениями соответствующих узловых перемещений КЭ (рис. 4.6).
РАМНЫЙ КОНЕЧНЫЙ ЭЛЕМЕНТ
 Рамный КЭ (рис. 4.7) применяется для моделирования стержней конструкции, находящихся в состоянии растяжения-сжатия и поперечного изгиба. Для воспроизведения такого состояния в качестве узловых перемещений рамного КЭ принимаются продольные перемещения
Рамный КЭ (рис. 4.7) применяется для моделирования стержней конструкции, находящихся в состоянии растяжения-сжатия и поперечного изгиба. Для воспроизведения такого состояния в качестве узловых перемещений рамного КЭ принимаются продольные перемещения 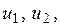 прогибы
прогибы 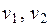 и углы поворота (обобщенные перемещения)
и углы поворота (обобщенные перемещения) 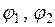 его узлов. Порядок следования данных перемещений определяется вектором
его узлов. Порядок следования данных перемещений определяется вектором 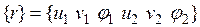 . Считается, что в пределах элемента погонные нагрузки
. Считается, что в пределах элемента погонные нагрузки 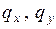 и жесткости
и жесткости 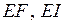 постоянны по его длине.
постоянны по его длине.
От перемещений 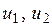 в поперечных сечениях элемента возникает только продольная сила
в поперечных сечениях элемента возникает только продольная сила 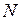 , от
, от 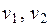 ,
, 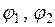 - только поперечная сила
- только поперечная сила 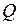 и изгибающий момент
и изгибающий момент 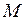 . Таким образом, состояния растяжения-сжатия и поперечного изгиба элемента являются независимыми. Это дает возможность сформировать матрицу жесткости
. Таким образом, состояния растяжения-сжатия и поперечного изгиба элемента являются независимыми. Это дает возможность сформировать матрицу жесткости 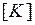 рамного КЭ из коэффициентов жесткости рассмотренных ранее ферменного и балочного элементов (расположение этих коэффициентов соответствует порядку следования узловых перемещений в векторе
рамного КЭ из коэффициентов жесткости рассмотренных ранее ферменного и балочного элементов (расположение этих коэффициентов соответствует порядку следования узловых перемещений в векторе 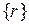 , как показано сверху и справа от матрицы
, как показано сверху и справа от матрицы 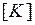 ):
):
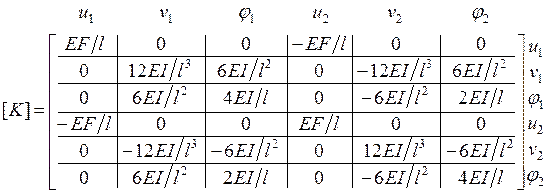 .
.
Аналогично формируется вектор нагрузки рамного КЭ:
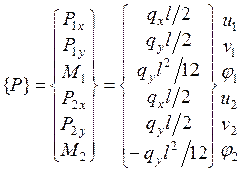 .
.
Положительные направления и порядок следования внешних узловых сил в векторе 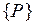 совпадают с положительными направлениями и порядком соответствующих узловых перемещений КЭ (рис. 4.7).
совпадают с положительными направлениями и порядком соответствующих узловых перемещений КЭ (рис. 4.7).

ТРЕУГОЛЬНЫЙ КОНЕЧНЫЙ ЭЛЕМЕНТ ПРИ ПЛОСКОМ НАПРЯЖЕННОМ
СОСТОЯНИИ
Треугольный КЭ при плоском напряженном состоянии (ПНС) (рис. 4.8) используется для моделирования пластин, нагруженных в их плоскости, а также безмоментных оболочек. Считается, что в пределах элемента поверхностные силы 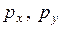 и толщина
и толщина 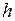 имеют постоянные значения.
имеют постоянные значения.
Представим перемещение 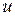 произвольной точки элемента в виде
произвольной точки элемента в виде 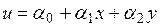 . Постоянные
. Постоянные 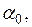
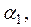
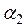 определяются из условий:
определяются из условий: 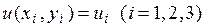 . Это дает систему уравнений
. Это дает систему уравнений
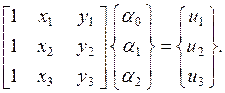
Для решения данной системы используем определители:
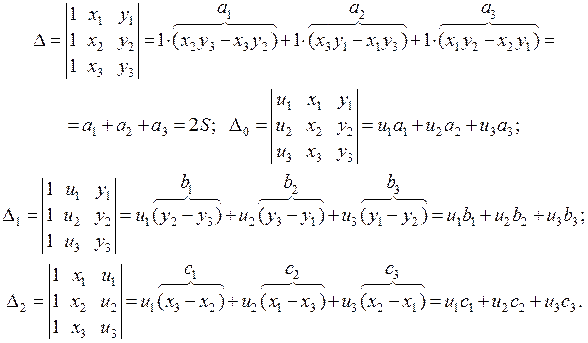
Отсюда получаем
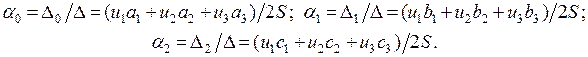
Здесь 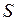 - площадь элемента (
- площадь элемента ( 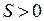 , если узлы 1, 2, 3 элемента следуют против хода часовой стрелки).
, если узлы 1, 2, 3 элемента следуют против хода часовой стрелки).
Подставляя 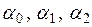 в выражение для
в выражение для 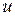 , получаем
, получаем
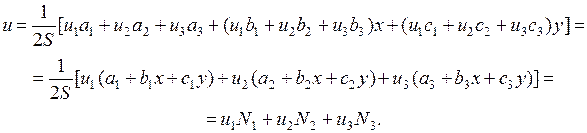
Здесь 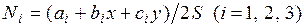 - функции распределения.
- функции распределения.
В аналогичном виде (через те же функции 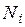 ) можно представить перемещение
) можно представить перемещение 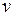 :
: 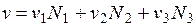 . Полученные выражения для перемещений
. Полученные выражения для перемещений 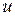 и
и 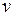 можно записать в виде одного матричного равенства:
можно записать в виде одного матричного равенства:
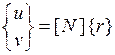 , (4.3.6)
, (4.3.6)
где
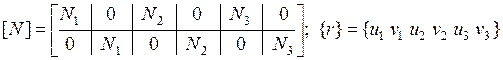
- соответственно матричная функция распределения и вектор узловых перемещений КЭ.
Перейдем к определению полной потенциальной энергии КЭ:
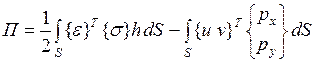 . (4.3.7)
. (4.3.7)
Здесь 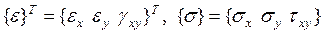 - соответственно матрица-строка и матрица-столбец с компонентами деформированного и напряженного состояний в произвольной точке КЭ. Векторы
- соответственно матрица-строка и матрица-столбец с компонентами деформированного и напряженного состояний в произвольной точке КЭ. Векторы 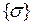 и
и 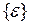 связаны физической зависимостью (обобщенным законом Гука)
связаны физической зависимостью (обобщенным законом Гука)
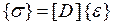 , (4.3.8)
, (4.3.8)
где 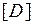 - матрица упругих свойств материала, зависящая от типа материала и его напряженного состояния. Материал принимается изотропным, а напряженное состояние его, как отмечено выше, считается плоским. В этом случае
- матрица упругих свойств материала, зависящая от типа материала и его напряженного состояния. Материал принимается изотропным, а напряженное состояние его, как отмечено выше, считается плоским. В этом случае
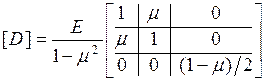 .
.
С учетом (4.3.8) и постоянства 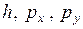 выражение (4.3.7) можно представить в виде
выражение (4.3.7) можно представить в виде
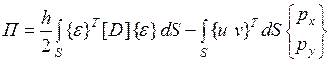 .
.
Деформации 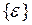 определяются через перемещения
определяются через перемещения 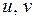 :
:
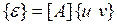 .
.
Оператор 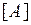 при плоском напряженном состоянии имеет вид
при плоском напряженном состоянии имеет вид
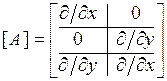 .
.
Для перехода от перемещений 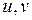 к узловым перемещениям
к узловым перемещениям 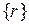 конечного элемента воспользуемся аппроксимацией (4.3.6):
конечного элемента воспользуемся аппроксимацией (4.3.6):
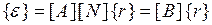 .
.
Таким образом, полная потенциальная энергия 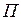 в конечном итоге представляется как функция узловых перемещений КЭ:
в конечном итоге представляется как функция узловых перемещений КЭ:
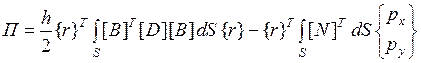 .
.
Отсюда получаем вариационное уравнение Лагранжа
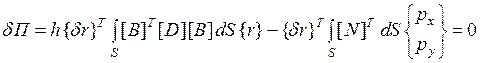 ,
,
из которого следует матричное уравнение равновесия внутренних и внешних узловых сил конечного элемента
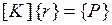 ,
,
где 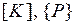 - соответственно матрица жесткости и вектор нагрузки данного элемента:
- соответственно матрица жесткости и вектор нагрузки данного элемента:
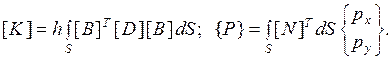
Определим матрицу 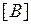 :
:
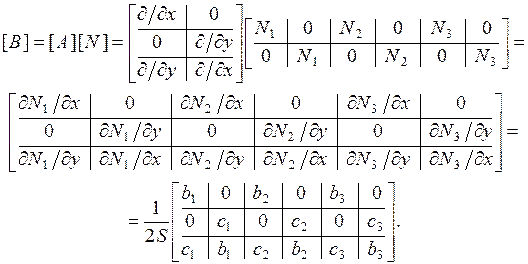
Отсюда видно, что матрица 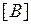 в пределах элемента постоянна. С учетом этого выражение для вычисления матрицы
в пределах элемента постоянна. С учетом этого выражение для вычисления матрицы 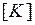 окончательно будет таким:
окончательно будет таким:
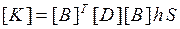 .
.
Найдем вектор 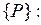
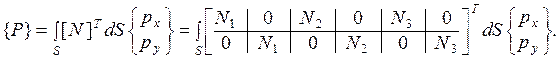
Функции 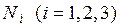 линейно зависят от координат
линейно зависят от координат 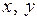 и обладают свойствами: в узле 1
и обладают свойствами: в узле 1 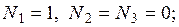 в узле 2
в узле 2 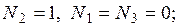 в узле 3
в узле 3 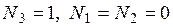 . Определенные интегралы
. Определенные интегралы 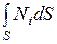 вычисляются исходя из их геометрического смысла: каждый интеграл
вычисляются исходя из их геометрического смысла: каждый интеграл 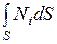 - есть объем пирамиды с единичной высотой и основанием
- есть объем пирамиды с единичной высотой и основанием 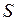 (рис. 4.9). Отсюда
(рис. 4.9). Отсюда 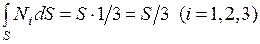 . С учетом этого получаем окончательное выражение для вычисления вектора
. С учетом этого получаем окончательное выражение для вычисления вектора 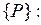

Дата добавления: 2016-07-27; просмотров: 2831;











