Позиционные системы счисления

В настоящее время наиболее распространенным принципом образования систем счисления является позиционный, при котором значение (вес) каждого символа зависит от его положения (позиции) в ряду символов, представляющих число. Самый младший разряд располагается в конце кодовой комбинации и имеет вес, равный единице, если отображаемое число является целым (в дальнейшем рассматривается кодирование только целых чисел). Вес единицы каждого следующего разряда больше веса предыдущего в m раз, где m – основание системы счисления (m указывает на число единиц какого-либо разряда, объединяемых в единицу более старшего разряда). Полное число получается в результате суммирования по всем разрядам:

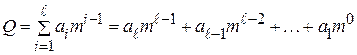(2.1)

где 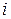– номер разряда; 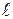– количество разрядов; 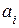– коэффициент, принимающий любые целочисленные значения в пределах от 0 до 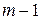и показывающий, сколько единиц i-го разряда содержится в числе.

Кодовая комбинация, отображающая число Q, записывается в виде последовательности коэффициентов :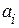

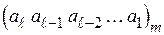(2.2)

Для указания того, в какой системе счисления записано число, принято при его изображении основание системы счисления указывать в виде нижнего индекса при нем.

В современном мире наиболее распространенным является представление чисел посредством арабских цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Позиционные системы счисления различаются выбором базисных чисел .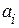

В десятичной системе ( 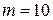) 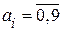. В соответствии с (2.1) кодовые комбинации нужно читать так:

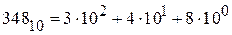
В восьмеричной системе .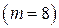

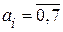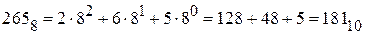
В шестнадцатеричной системе 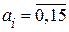. Как и в предыдущих системах счисления, для обозначения первых десяти базисных чисел здесь используются арабские цифры, а для изображения цифр, больших 9, применяются буквы: А = 10, В = 11, С = 12, D = 13, Е = 14, F = 15.

В двоичной системе .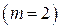

.

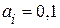Чем больше основание системы счисления, тем меньше количество разрядов требуется для представления данного числа, а, следовательно, тем меньше времени требуется для его передачи и меньше объем запоминающего устройства для хранения. Однако с ростом основания существенно повышаются требования к линиям связи и аппаратуре распознавания сигналов. Кроме этого, арифметические и логические элементы вычислительных устройств должны иметь большое число устойчивых состояний. В связи с этими обстоятельствами в современной вычислительной технике, в устройствах автоматики и связи широко используется двоичная система счисления. Логические элементы, соответствующие этой системе, должны иметь всего два устойчивых состояния. Задача различения сигналов, отображающих символы, сводится в этом случае к задаче обнаружения (есть сигнал или нет его), что значительно проще. Просто выполняются арифметические операции:

+

=

-

=

=

+

=

-

=

=

+

=

-

=

=

+

=

-

=

=

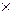
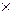
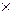
Наиболее распространенная при кодировании и декодировании логическая операция – суммирование по модулю. При она также наиболее проста и определяется равенствами:

			=						=
			=						=

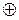
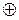
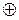
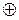
Все вышеперечисленное является причиной того, что большинство современных ЭВМ используют двоичную систему счисления.

Неудобство использования двоичного кода заключается в громоздкости записи чисел. Поэтому если возникает необходимость кодирования информации «вручную», например, при составлении программы на машинном языке, то предпочтение отдается восьмеричной или шестнадцатеричной системам.

Кроме этого, двоичный код неудобен при вводе и выводе информации, т.к. трудно оперировать с непривычными двоичными числами. Человек привык работать и легко ориентируется при использовании десятичного кода. Для устранения этого неудобства применяется двоично-десятичный код, являющийся одним из вариантов смешанной системы счисления.