Условия наивыгоднейшего распределения активных нагрузок

1. Между параллельно работающими агрегатами одной электростан­ции (блоки КЭС, турбогенераторы и парогенераторы ТЭЦ с общим паро­проводом, гидроагрегаты ГЭС) активная нагрузка должна распределяться по условиям:

(5.2)

где – удельный («относительный» – у многих авторов) прирост рас­хода энергоносителя i-го агрегата, определяет изменение расхода энергоно­си­теля в единицу времени B_i (т.у.т/ч, Гкал/ч, м³/с) при изменении нагрузки агре­гата Р_i на одну единицу; для всех агрегатов b_i >0;

Р_i, P_ЭС.уст – нагрузка i-го агрегата и суммарная нагрузка, заданная всем n агрегатам;

Р_{i min} ÷ Р_{i max} – диапазон допустимых нагрузок i-го агрегата.

Справедливость равенства удельных приростов как условия наивыгод­нейшего распределения подтверждается простым «мысленным» эксперимен­том. Пусть параллельно работают два агрегата с нагрузками Р₁ и Р₂, причем b₁<b₂, .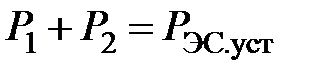

Не изменяя заданной нагрузки P_ЭС.уст, увеличим нагрузку 1-го агрегата и уменьшим 2-го на 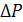. При этом изменится расход энергоносителя:

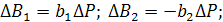
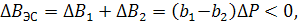
т.е. получим экономию.

Такое перераспределение для любого количества агрегатов, очевидно, вы­годно вести до тех пор, пока удельные приросты сравняются.

Для оптимизации распределения P_ЭС.уст по условиям (5.2) пользуются ха­рактеристиками удельного («относительного») прироста – зависимостями b_i(P_i), получаемыми путем графического дифференцирования расходной ха­рактеристики агрегата B_i(P_i).

По характеристикам УП отдельных агрегатов можно построить характе­ристики УП нескольких агрегатов при их последовательном соединении (рис. 5.2,а), параллельном (рис. 5.2,б) и для электростанции в целом.

Рис. 5.2. Последовательное (а) и параллельное (б) соединение агрегатов

При последовательном соединении агрегатов

,

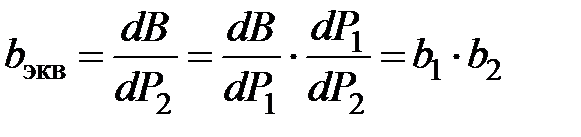при параллельном

.

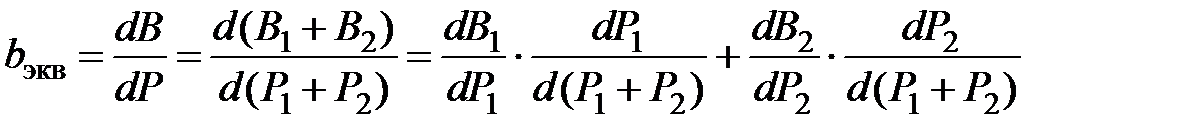Поскольку при наивыгоднейшем распределении

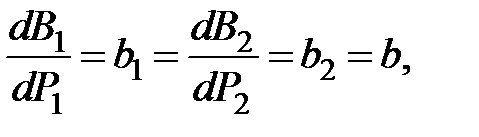
то

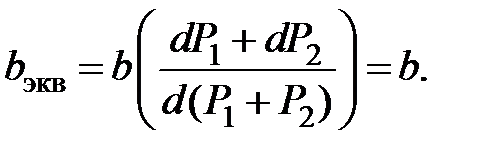
Для электростанции в целом строятся зависимости

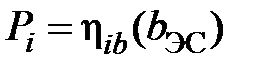или ,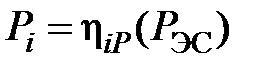

которые используются для задания мощности каждому агрегату Р_i по задан­ному удельному приросту ЭС – b_ЭС или по заданной мощности ЭС – Р_ЭС.

2. Между тепловыми электростанциями в сосредоточенных (концен­три­рованных) энергосистемах с короткими линиями, когда потерями актив­ной мощности в сетях можно пренебречь, активная нагрузка должна распре­де­ляться по условию уравнивания удельных приростов часовой стоимости затрат на топливо (удельных приростов переменной составляющей издер­жек), а не удельных приростов часового расхода условного топлива, так как стоимость одной тонны условного топлива на различных ТЭС различна:

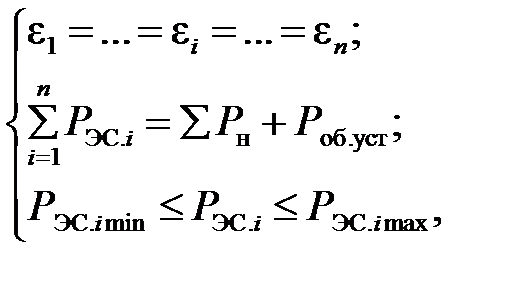(5.3)

где 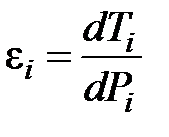– удельный прирост часовой стоимости затрат (издержек) i-й элек­тростанции;

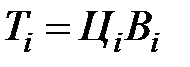– часовая стоимость затрат (топливная составляющая) на выра­ботку мощности Р_i, т. е.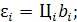

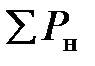, P_об.уст– суммарная нагрузка ЭЭС и задаваемая обменная мощность по всем связям с другими ЭЭС;

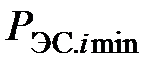, – диапазоны допустимых нагрузок i-й ЭС при заданном со­ставе включенного оборудования.

3. Между тепловыми электростанциями в рассредоточенных энерго­сис­темах, когда потерями активной мощности в сетях пренебречь нельзя, распределение активной нагрузки должно производиться с учетом этих по­терь по условиям:

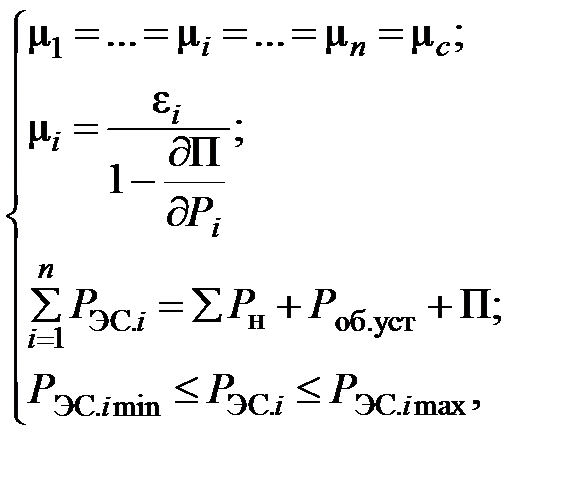(5.4)

где 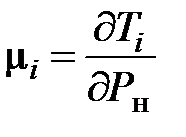– удельный прирост затрат i-й электростанции при изменении на­грузки энергосистемы в балансирующей точке Р_н на одну единицу и не­измен­ной мощности остальных электростанций;

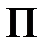– суммарные потери активной мощности в основных сетях энергосис­темы;

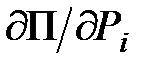– удельный прирост потерь при изменении мощности только i-й электростанции.

Выражение для µ_i в (5.4) можно получить простыми рассуждениями. Уве­личим нагрузку i-й электростанции на малую величину . Нагрузка баланси­рующей точки должна быть изменена при этом на 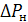. Чтобы час­тота в энерго­системе не изменилась, должен сохраняться баланс мощностей:

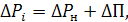
где 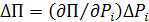– приращение потерь в сетях.

Отсюда

,

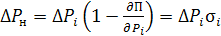где 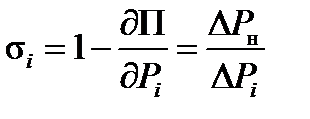– доля полезно используемого приращение мощности на i-й электростанции. Прирост затрат на i-й электростанции ( и в энерго­системе) составит при этом

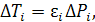
а удельный прирост затрат – на единицу полезно отпущенной мощности, т.е. с учетом потерь в сетях:

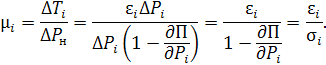
Если величины µ_i не одинаковы для каких-либо двух электростанций, то можно получить экономию в энергосистеме, увеличив нагрузку станции с меньшим значением µ_i и соответственно снизив нагрузку станции с бо́льшим значением. Оптимальный режим наступит тогда, когда нагрузки электростан­ций перераспределятся так, что удельные приросты затрат с уче­том потерь в сетях – µ_i сравняются.

4. Между тепловыми и гидравлическими электростанциями (АЭС ра­ботают в базовом режиме и к регулированию не привлекаются) в смешан­ной рассредоточенной энергосистеме распределение нагрузки необходимо произ­водить так, чтобы за расчетный период (цикл регулирования) при за­данном расходе воды турбинами ГЭС, который определяется по прогнозу притока воды и расхода для судоходства, орошения и т.п., затраты тепловых электро­станций были минимальными.

Для экономичного распределения нагрузки в этом случае необходимо не­прерывно соблюдать условия:

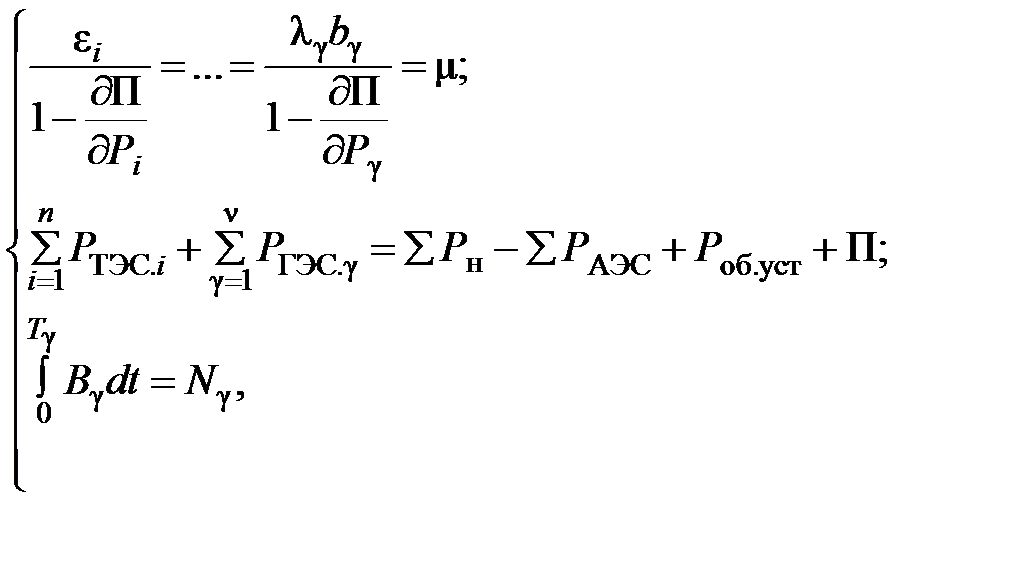(5.5)

где i=1…n – индекс тепловой электростанции;

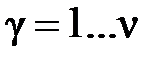– индекс гидравлической электростанции;

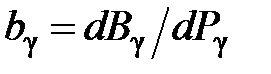– удельный прирост часового расхода воды 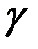-й ГЭС;

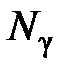– заданный расход воды 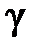-й ГЭС за период .

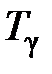Размерность коэффициента :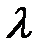

.

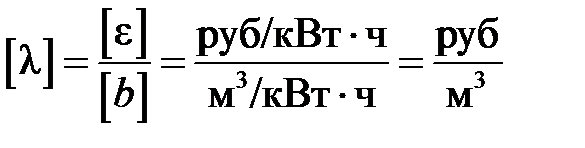Значение коэффициента 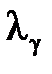определяет изменение затрат тепловых элек­тро­станций при изменении пропуска воды через турбины 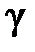-й ГЭС на еди­ницу.

Величину λ называют неопределенным множителем Лагранжа. Его предварительно рассчитывают для каждой ГЭС на период 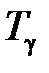, исходя из пред­полагаемых графи­ков нагрузки, так чтобы расход воды на ГЭС за рас­четный период 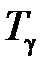имел заданное значение 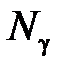, а затем периодически коррек­тируют. Неоправ­данно заниженное значение коэффициента 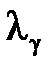приве­дет к тому, что электриче­ская нагрузка 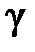-й ГЭС будет задаваться слишком большой, что в свою оче­редь приведет к снижению напора и затоплению нижнего бьефа и наоборот.

Расчет коэффициентов 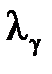и удельных приростов потерь в сетях 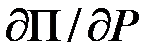для каждой ЭС выполняется для различных режимов работы энергосистемы по специальным программам на ЭВМ.

5. Между объединениями, входящими в единую энергосистему, распре­де­ление нагрузки определяется заданным (согласованным) графиком сум­марной обменной мощности P_об.уст=f(t) для каждого объединения. Собст­венная генерация объединения должна покрывать свою нагрузку, потери в сетях и обеспечивать заданное значение обменной мощности – второе урав­не­ние в (5.5).

Рассмотренные условия наивыгоднейшего распределения активных на­грузок реализуются при вторичном или третичном регулировании.