Характеристики движения тела, брошенного под углом к горизонту, по двум осям (ось Y направлена вверх)

Характеристики	Ось Х	Ось Y
Начальная скорость	v0x = v0·cos(θ0)	v0y = v0 ∙ sin (θ0).
Ускорение		— g
Время полета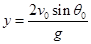
Дальность полета для случая, когда точки броска и приземления находятся на одной высоте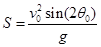
Максимальная высота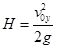
Скорость в момент t	vx = v0x	vy = v0y—gt
Координаты в момент t	х = vx .t	y = v0y ∙ t -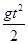

Максимальная высота подъема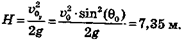

Полет пули

Из автомата производят выстрел в горизонтальном направлении (q₀ = 0). Начальная скорость пули v₀ = 715м/с. Расстояние до мишени х = 100 м. В нашем случае v_x – v_0x = v₀ = 715 м/с; v_0y = 0.

Из уравнения х = v_x∙t найдем t = 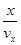= 0,14с Координата точки мишени, в которую попадет пуля, находится из уравнения y= v_0y ∙t 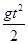= -0,1 м. Таким образом пуля опустится на 10 см. Чтобы скомпенсировать такое опускание, выстрел производят под небольшим углом вверх, для чего соответствующим образом устанавливают прицел.

Прыжок в длину с разбега (рис. 3.18)

Оценим теоретическую максимальную дальность прыжка в длину, определяемую физическими возможностями человека. Горизонтальную скорость v_0x спортсмен набирает при разбеге.

Примем ее равной максимальной скорости спринтера: v_0x = 10,5 м/с. Вертикальную скорость v₀ спортсмен приобретает при отталкивании. Оценим ее исходя из того, что высота, на которую человек может поднять свой центр масс, прыгая вертикально вверх с места, приблизительно равна 0,6 м. Из формулы

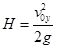
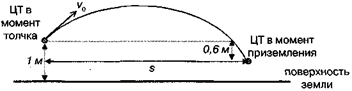
Рис.3.18. К описанию прыжка в длину с разбега

Найдем v_0y = 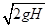= 3,43 м/с. Прыгун отталкивается в вертикальном положении, а приземляется в «сидячем» положении. При этом центр масс опускается приблизительно на 0,6 м (при отталкивании центр масс находится на высоте ~1 м, а при приземлении на высоте ~0,4 м). Значит координата точки приземления у 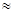-0,6 м.

Эта координата определяется формулой 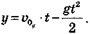Подставив численные значения, получим квадратное уравнение: 4,9-t² — 3,43∙t — 0,6 = 0. Решив его, найдем время полета t = 0,845 с. Дальность прыжка найдем из формулы s = v_x ∙t = 8,87 м.