Пример: Ситуация «Охотник».

Состояние среды: h₁ – заяц есть; h₂ – зайца нет.

Гипотезы: H₁ – заяц есть; H₂ – зайца нет.

Априорная информация: Среди охотников прошел слух: «В лесу зайцев видимо–невидимо!». Жители окрестных деревень, видевшие много охотников (и собравшие «статистику»), говорят: «Заяц есть! Каждые 9 из 10 охотников возвращаются с зайцем».

Апостериорная информация: e_j – шорох в кустах, который слышит охотник.

Априорные вероятности: q₁=0,9 – вероятность, с которой охотник ожидает встретить зайца; q₂=0,1 - вероятность, с которой охотник ожидает его не встретить. (q₁+q₂=1).

Апостериорные вероятности: p(e_j /h₁)=0,2 – вероятность того, что данный шорох в кустах вызван зайцем; p(e_j/h₂)=0,8 - вероятность того, что данный шорох имеет другую причину (ветер, мышь и пр.).

Порог принятия решения: λ₀ = 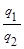= = 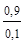9.

Отношение правдоподобия: λ(e_j)= 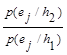= = 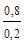4.

Принятие решения: Применяя сформулированное выше правило принятия решения, получаем: λ(e_j) < λ₀ (т.к. 4<9), что означает принятие гипотезы H₁ – «Заяц есть!» и выполнение соответствующего действия: «Стрелять!».

В случае получения охотником другой априорной информации могут измениться априорные вероятности, из-за чего изменится порог принятия решения и, как следствие, может быть принято другое решение: Например, жители окрестных деревень говорят охотнику: «Заяц не то чтобы он есть, но и не то, чтобы его не было». Тогда:

Априорные вероятности: q₁=q₂=0,5.

Порог принятия решения: λ₀=1.

Принятие решения: в той же ситуации имеем λ(e_j) >λ₀ (т.е. 4>1), следовательно, принимается гипотеза H₂ - «Зайца нет!» - и охотник воздерживается от выстрела.

3.1.2. Стратегия принятия решения

Введем обозначения, которые будут использоваться в задаче измерения чувствительности сенсорной системы, и рассмотрим случай измерения абсолютной чувствительности:

- состояние среды: h₁- стимул есть в пробе - обозначаем это S (от английского термина «Stimulus» - «Стимул»);

h₂-стимула нет в пробе - обозначаем n . (от английского термина «noise» - «шум»);

- гипотезы : H₁ - «стимул в пробе есть»;

H₂ - «стимула в пробе нет»;

- ответы испытуемого:R₁- ответ «стимул есть» - обозначаем Y (от «Yes»);

R₂ - ответ «стимула нет» - обозначаем N. (от «No»).

Все возможное множество сочетаний возможных состояний среды h и ответов испытуемого R в этом случае может быть представлено простой четырехклеточной матрицей:

Таблица 4