Определение подгруппы.
Непустое подмножество 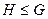 группы
группы 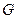 называется подгруппой, если само
называется подгруппой, если само 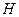 является группой относительно операции, введённой в группе
является группой относительно операции, введённой в группе 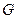 .
.
Примеры.
Крайние случаи:
1) сама группа есть подгруппа, 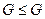 .
.
2) множество, состоящее только из нейтрального элемента, 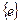 .
.
Пример. 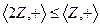 , все чётные числа. 0 нейтральный как в самой
, все чётные числа. 0 нейтральный как в самой 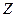 , так и в подгруппе.
, так и в подгруппе.
Впрочем, подгруппой является любое подмножество вида 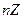 .
.
Пример. Подмножество 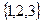 подгруппой не является, т.к. результат сложения может быть и больше 3, т.е. выводит за пределы этого множества.
подгруппой не является, т.к. результат сложения может быть и больше 3, т.е. выводит за пределы этого множества.
Примеры. 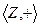
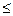
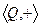
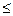
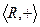
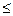
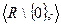
Пример. Конечная группа, дана таблица умножения элементов:
Похоже на то, что было при изучении подстановок, только не унарная, а бинарная операция. Есть 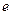 , это 1. Для каждого есть обратный. Для 2 это 3, для 3 это 2. В каждой строке (и каждом столбце) перестановка из трёх различных чисел.
, это 1. Для каждого есть обратный. Для 2 это 3, для 3 это 2. В каждой строке (и каждом столбце) перестановка из трёх различных чисел.
--- перерыв ---
Теорема 1 (критерий подгруппы).
Непустое подмножество 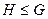 группы
группы 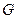 является подгруппой
является подгруппой 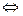
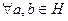 выполняется:
выполняется: 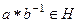 .
.
Доказательство.
1. Необходимость- очевидно, по определению, если 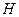 сама является группой, то
сама является группой, то 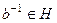 ,
, 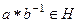 .
.
2. Достаточность.Если 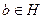 , то
, то 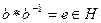 .
.
Тогда для всякого 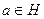 , обратный также принадлежит, ведь
, обратный также принадлежит, ведь 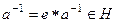 . □
. □
Примечание.Этот критерий - фактически эквивалентное свойство, которое могло бы быть принято в качестве определения подгруппы.
Теорема 2.Если 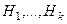 - подгруппы группы
- подгруппы группы 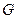 , то их пересечение
, то их пересечение
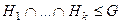 тоже подгруппа.
тоже подгруппа.
Доказательство. Если 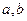
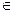
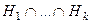 , то
, то 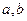
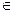 всем
всем 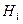 .
.
Но каждая 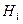 подгруппа, так что
подгруппа, так что 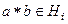 (всем), а значит, их пересечению. Кроме того,
(всем), а значит, их пересечению. Кроме того, 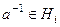 для всех номеров
для всех номеров 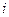 , а значит, тоже
, а значит, тоже 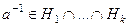 . В итоге,
. В итоге, 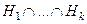 подгруппа. □
подгруппа. □
Пример. Подгруппы 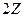 и
и 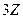 , а их пересечение
, а их пересечение 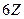 - все числа, кратные 6.
- все числа, кратные 6.
Пример. Группа подстановок 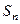 называется симметрической группой степени n. Число элементов
называется симметрической группой степени n. Число элементов 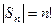
1) Ассоциативность есть.
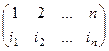 ,
, 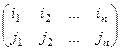 ,
, 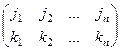 .
.
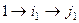 а затем
а затем 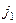 переходит в
переходит в 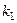 , в итоге
, в итоге 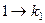 .
.
С другой стороны, 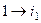 а
а 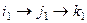 в результате композиции 2-й и 3-й подстановок, в итоге опять
в результате композиции 2-й и 3-й подстановок, в итоге опять 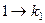 .
.
2) Нейтральный элемент 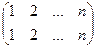 .
.
3) Обратный элемент.
Если 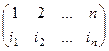 то обратный
то обратный 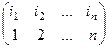 , где в верхней строке все n разных чисел и их можно расставить по порядку.
, где в верхней строке все n разных чисел и их можно расставить по порядку.
Пример.Подгруппа 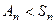 - группа всех чётных подстановок. Кол-во элементов
- группа всех чётных подстановок. Кол-во элементов 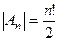 .
.
Пример. Подмножество всех нечётных подстановок - не образует подгруппу, потому что: произведение подстановки и обратной к ней (обе нечётные) это тождественная подстановка, а она содержит 0 инверсий, значит - чётная, но тогда она не принадлежит этому подмножеству.
Пример. Группы движений и симметрий правильных n-угольников.
Например, для треугольника. Каждый поворот или зеркальное отражение, при котором 3 вершины переходят в какие-то другие, соответствует подстановке.
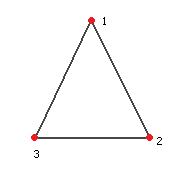
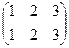
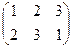
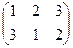 вращения
вращения
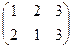
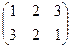
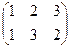 зеркальные отражения
зеркальные отражения
Но при этом можно заметить, что всякое отражение может быть получено как композиция какого-то одного базового отражения (например, где меняются вершины 1 и 2) и поворота.
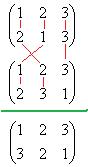
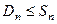 называется группой Диэдра. Для
называется группой Диэдра. Для 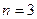 (в случае треугольника) она совпадает с группой всех подстановок,
(в случае треугольника) она совпадает с группой всех подстановок,
Для 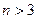 , уже
, уже 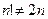 .
.
Кольца
Теперь рассмотрим множества не с одной, а с двумя различными операциями. Интуитивно вам уже известны такие примеры: сложение и умножение на множестве чисел, к тому же, для них известен закон дистирибутивности: 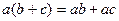 ,
, 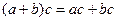 .
.
Определение. Пусть 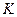 - множество, на котором заданы две бинарные операции (как правило, сложение и умножение), удовлетворяющие условиям:
- множество, на котором заданы две бинарные операции (как правило, сложение и умножение), удовлетворяющие условиям:
1) 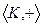 абелева группа
абелева группа
2) 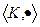 полугруппа (т.е. только ассоциативность)
полугруппа (т.е. только ассоциативность)
3) операции сложения и умножения связаны законами дистрибутивности: 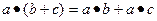 ,
, 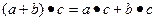 .
.
Тогда 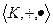 называется кольцом.
называется кольцом.
Если существует нейтральный элемент по умножению, то кольцо называется кольцом с единицей. Если операция умножения коммутативна, то называется «коммутативное кольцо».
Примеры.
1)Числовые кольца. 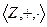 ,
, 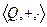 ,
, 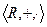 коммутативные кольца с единицей.
коммутативные кольца с единицей.
2) Кольцо функций. Функции, заданные на 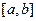 , можно поточечно складывать и умножать.
, можно поточечно складывать и умножать.
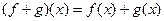 ,
, 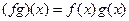 .
.
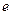 по сложению - тождественно нулевая функция
по сложению - тождественно нулевая функция 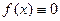 .
.
По сложению есть противоположный элемент.
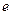 по умножению - тождественная
по умножению - тождественная 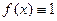 .
.
3) Множество векторов в 3-мерном пространстве относительно операции векторного умножения. Это пример некоммутативного кольца, и без единицы.
Лемма.
1. При умножении любого элемента на 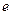 по сложению получится
по сложению получится 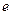 . То есть,
. То есть, 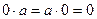 .
.
2. Произведение 1-го элемента на противоположный ко 2-му это то же самое, что произведение противоположного 1-му на 2-й, и равно противоположному к их суммарному произведению, т.е. 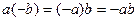 .
.
Доказательство.
1. 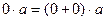 =
= 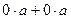 , вычтем
, вычтем 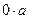 из обеих частей равенства, получим
из обеих частей равенства, получим 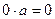 .
.
2. 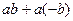 =
= 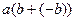 =
= 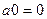
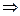
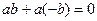
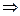
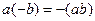 .
.
Дата добавления: 2020-11-18; просмотров: 663;











