Площади плоских фигур и объемы тел вращения
Если непрерывная линия задана уравнением 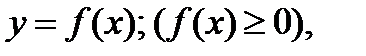 топлощадь криволинейной трапеции, ограниченной этой линией, двумя прямым
топлощадь криволинейной трапеции, ограниченной этой линией, двумя прямым 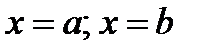 отрезком оси абсцисс а < х < b, вычисляется по формуле
отрезком оси абсцисс а < х < b, вычисляется по формуле
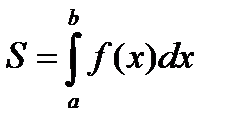 (3.17)
(3.17)
Пример 3.12. Вычислить площадь, ограниченную графиками функций: 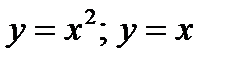
Решение.Построим графики данных функций, найдя предварительно точки их пересечения путем решения системы: 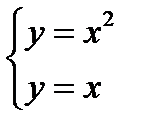 .Решив эту систему, получим точки O(0; 0) и A(1; 1).
.Решив эту систему, получим точки O(0; 0) и A(1; 1).
|
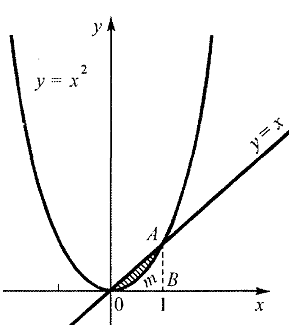
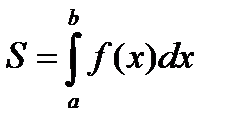 предполагает вычисление площади, ограниченной графиком функции
предполагает вычисление площади, ограниченной графиком функции 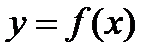 , осью х и прямыми
, осью х и прямыми 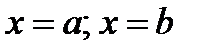 . В данной задаче, взяв
. В данной задаче, взяв 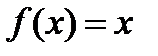 , мы вычислим площадь треугольника ОАВ, а взяв
, мы вычислим площадь треугольника ОАВ, а взяв 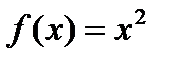 , вычислим площадь криволинейного треугольника
, вычислим площадь криволинейного треугольника 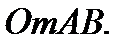 Затем из первого результата вычтем второй. Итак,
Затем из первого результата вычтем второй. Итак,
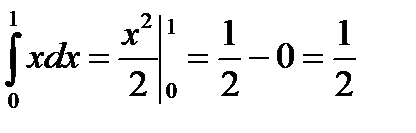 и
и 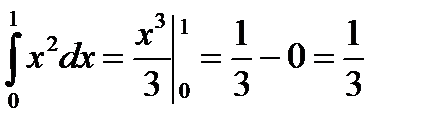
Следовательно, площадь S фигуры, ограниченная заданными линиями
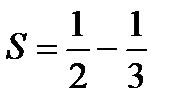 кв.ед.
кв.ед.
Пример 3.13.Вычислить площадь, ограниченную линией 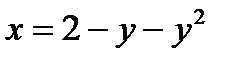 и осью ординат.
и осью ординат.
Решение.В этом примере искомая площадь ограничена линией 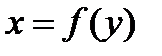 и может
и может 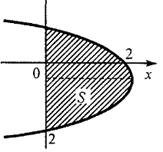 быть вычислена с помощью интеграла
быть вычислена с помощью интеграла 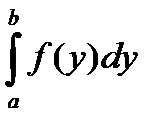 , где а и b -ординаты точек пересечения данной кривой с осью ординат. Найдем эти ординаты из системы:
, где а и b -ординаты точек пересечения данной кривой с осью ординат. Найдем эти ординаты из системы:
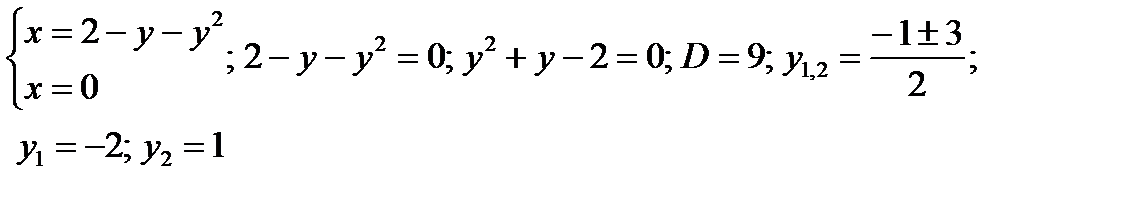
Следовательно, 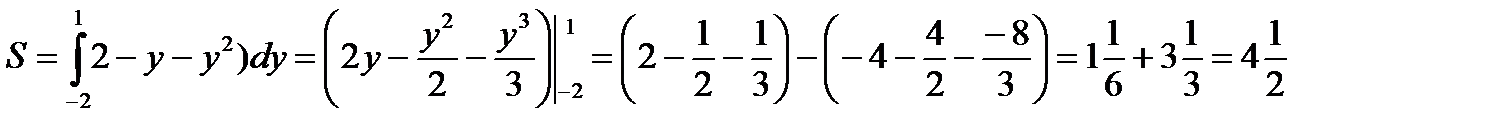 (кв.ед.).
(кв.ед.).
Пример 3.14.На схеме, в системе координат Оху, излучина реки образует кривую 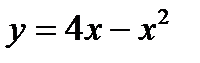 . По оси
. По оси 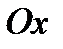 проходит шоссе. Найдите координаты пересечения реки и шоссе и вычислите, какую площадь занимает пашня между рекой и линией шоссе.
проходит шоссе. Найдите координаты пересечения реки и шоссе и вычислите, какую площадь занимает пашня между рекой и линией шоссе.
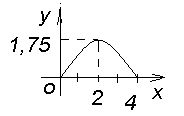 Решение.Определим координаты точек пересечения кривой и оси
Решение.Определим координаты точек пересечения кривой и оси 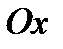 из системы уравнений:
из системы уравнений: 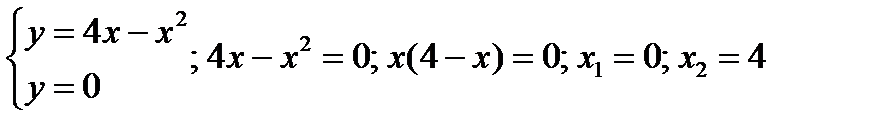 (см. рис.).
(см. рис.).
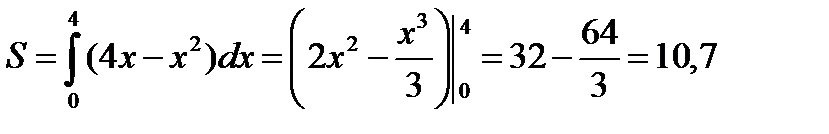
Пример 3.15.Вычислите площадь фигуры, ограниченной линиями: 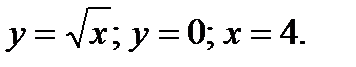
Решение. 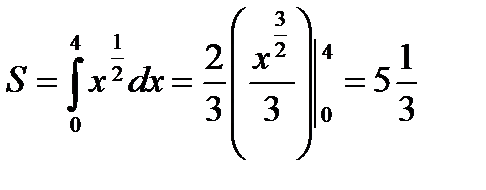
Если криволинейная трапеция, ограниченная линией 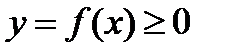 и прямыми
и прямыми 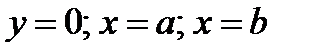 , вращается вокруг оси х, то объем тела вращения вычисляется по формуле:
, вращается вокруг оси х, то объем тела вращения вычисляется по формуле: 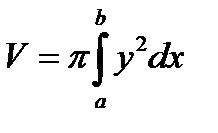 (3.18)
(3.18)
Если фигура, ограниченная линиями 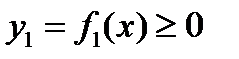 и
и 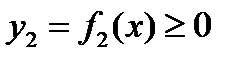
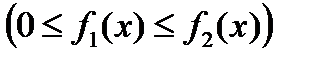 прямыми
прямыми 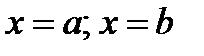 , вращается вокруг оси Oх, то объем тела вращения вычисляется по формуле:
, вращается вокруг оси Oх, то объем тела вращения вычисляется по формуле: 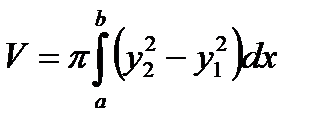 (3.19)
(3.19)
Пример 3.16 Найдите объем шара, полученного при вращении полукруга 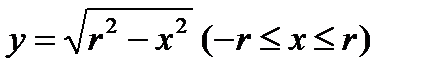 вокруг оси Ох.
вокруг оси Ох.
Решение. По формуле (3.18) имеем:
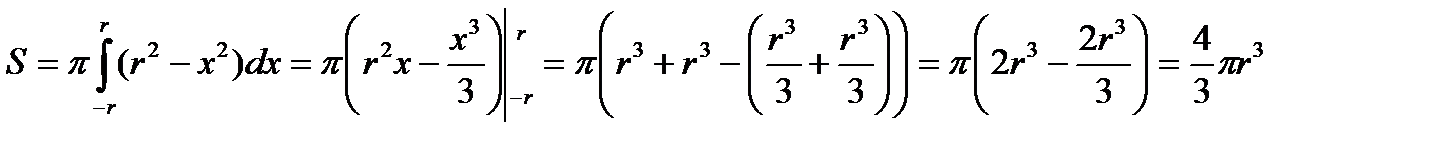
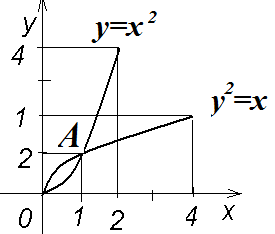 Пример 3.17. Найдите объем тел, образованных вращением вокруг оси Ох фигур, ограниченных линиями:
Пример 3.17. Найдите объем тел, образованных вращением вокруг оси Ох фигур, ограниченных линиями: 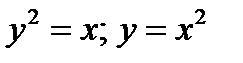
Решение. Определим координаты точки пересечения этих линий из системы: 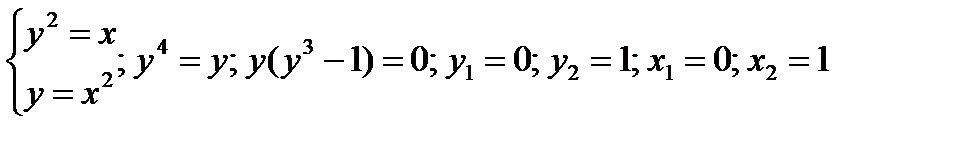 Таким образом, имеем две точки пересечения линий:
Таким образом, имеем две точки пересечения линий: 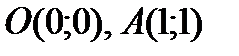 . По формуле (3.19) имеем:
. По формуле (3.19) имеем:
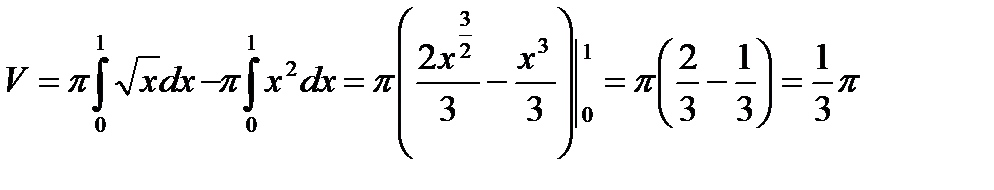
Дата добавления: 2020-11-18; просмотров: 595;











