НАЧАЛЬНАЯ ПОПЕРЕЧНАЯ ОСТОЙЧИВОСТЬ.

Теория продольной остойчивости позволяет рассчитать и предсказать дифферент судна и его посадку на тихой воде, что очень важно для экипажа при решении проблем загрузки судна, обеспечения прочности, определения количества груза на судне, безопасной его посадки, заливаемости, слемминга и т.д.

Теория поперечной остойчивости позволяет судоводителю:

-оценивать уровень безопасности мореплавания,

-планировать и осуществлять действия по распределению грузов и запасов на судне,

-выполнять необходимые расчеты по методикам контроля остойчивости Регистра судоходства и ИМО,

-обосновывать те или иные действия по изменению загрузки судна.

Кроме того, существует условное методическое разделение остойчивости на начальную остойчивость и остойчивость при больших наклонениях.

В первом случае удается за счет введения упрощающих предположений получить несложные расчетные формулы для некоторых важных величин, а во втором – применять графоаналитические методы при невозможности применения простых формул начальной остойчивости.

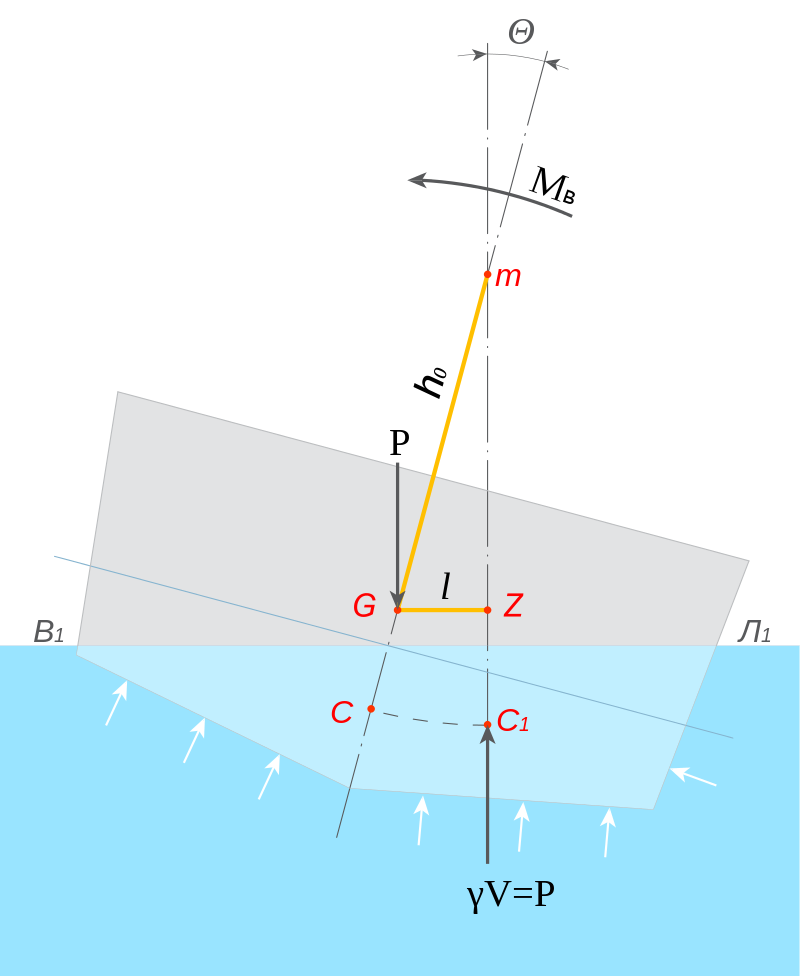
Рис. 139. Начальная поперечная остойчивость.

Остойчивостью называется способность судна противостоять, силам, вызвавшим его наклонение, и после прекращения действия этих сил возвращаться в первоначальное положение. Наклонения судна возможны по разным причинам: от действия набегающих волн, из-за несимметричного затопления отсеков при пробоине, от перемещения грузов, давления ветра, из-за приема или расходования грузов и пр.

. Представим себе, что под действием внешних сил судно получило крен на угол 9 (рис. 140). Вследствие этого объем подводной части судна сохранил свою величину, но изменил форму; по правому борту в воду вошел дополнительный объем, а по левому борту равновеликий ему объем вышел из воды. Центр величины переместился из первоначального положения С в сторону крена судна, в центр тяжести нового объема — точку С¹. При наклонном положении судна сила тяжести Р, приложенная в точке G, и сила поддержания D, приложенная в точке С, оставаясь перпендикулярными к новой ватерлинии В¹Л¹ образуют пару сил с плечом GK, являющимся перпендикуляром, опущенным из точки G на направление сил поддержания. Если продолжить направление силы поддержания из точки С¹ до пересечения с ее первоначальным направлением из точки С, то на малых углах крена, соответствующих условиям начальной остойчивости, эти два направления пересекутся в точке М, называемой поперечным метацентром. Расстояние между метацентром и центром величины МС называется поперечным метацентрическим радиусом, обозначаемым р, а расстояние между точкой М и центром тяжести судна G — поперечной метацентрической высотой h⁰. На основании данных рис. 140 можно составить тождество

h⁰ = p + z^c — z^g.

В прямоугольном треугольнике GMR угол у вершины М будет равен углу Θ. По его гипотенузе и противолежащему углу можно определить катет GK, являющийся плечо м восстанавливающей судно пары GK=h⁰ sin Θ, а восстанавливающий момент будет равен Мвосст = DGK. Подставляя значения плеча, получим выражение

Мвосст = Dh⁰ * sin Θ,

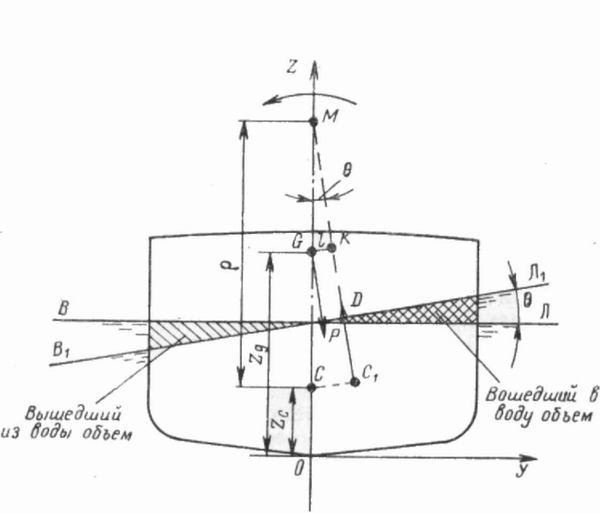Рис. 140. Силы, действующие при крене судна.

Взаимное положение точек М и G позволяет установить следующий признак, характеризующий поперечную остойчивость:

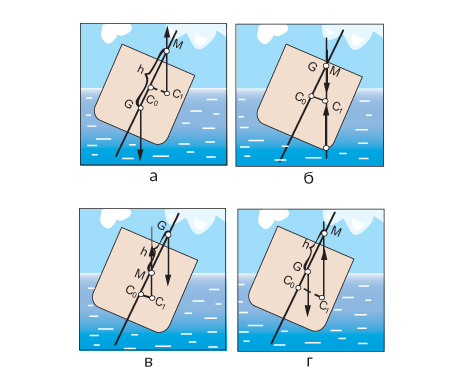
- если метацентр расположен выше центра тяжести, то восстанавливающий момент положителен и стремится вернуть судно в исходное положение, т. е. при накренении судно будет остойчиво, наоборот,

- если точка М находится ниже точки G, то при отрицательном значении h⁰ момент отрицателен и будет стремиться увеличивать крен, т. е. в этом случае судно неостойчиво.

Возможен случай, когда точки М и G совпадают, силы Р и D действуют по одной вертикальной прямой, пары сил не возникает, и восстанавливающий момент равен нулю: тогда судно надо считать неостойчивым, так как оно не стремится вернуться в первоначальное положение равновесия (рис. 141).

Если метацентр расположен выше центра тяжести, то судно остойчиво (его метацентрическая высота положительна, а восстанавливающий момент стремится устранить крен и вернуть судно в исходное прямое положение равновесия).

Если же (например, в результате переноса грузов из трюмов на палубу) центр тяжести судна окажется расположенным выше метацентра, то метацентрическая высота станет отрицательной, восстанавливающий момент также изменит свой знак и будет стремиться увеличить крен судна, которое становится неостойчивым. Однако это не означает, что оно при этом обязательно опрокинется, хотя возможность оп­рокидывания судна в результате возникновения отрицательной начальной остойчивости при определенных условиях не исключена.

При совпадении точек М и G судно также следует считать неостойчивым: оно будет плавать (в пределах малых углов крена) в состоянии безразличного равновесия.

Таким образом, физический смысл метацентра m заключается в том, что эта точка служит пределом, до которого можно поднимать центр тяжести судна, не лишая его положительной начальной остойчивости («мета» по-древнегречески означает «предел»).

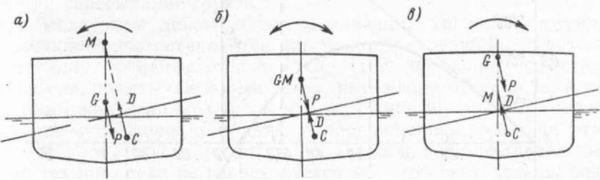
Рис. 141. Поперечная остойчивость судна в зависимости от расположения грузов: а — положительная остойчивость; б — положение равновесия — судно неостойчиво; в — отрицательная остойчивость.

Метацентрическую высоту для характерных случаев нагрузки вычисляют в процессе проектирования судна, и она служит мерой остойчивости. Значение поперечной метацентрической высоты для основных типов судов лежит в пределах 0,5—1,2 м и лишь у ледоколов достигает 4,0 м. Для увеличения поперечной остойчивости судна необходимо снижать его центр тяжести. Это чрезвычайно важный фактор всегда надо помнить, особенно при эксплуатации судна, и вести строгий учет за расходованием топлива и воды, хранящихся в междудонных цистернах.

Вопросам остойчивости судна придается исключительно важное значение, и поэтому обычно, кроме всех теоретических вычислений, после постройки судна проверяют истинное положение его центра тяжести путем опытного кренования, т. е. поперечного наклонения судна путем перемещения груза определенного веса, называемого кренбалластом . Все полученные ранее выводы, как уже упоминалось, практически справедливы при начальной остойчивости, т. е. при крене на малые углы. При расчетах поперечной остойчивости на больших углах крена (продольные наклонения на практике не бывают большими) определяют переменные положения центра величины, метацентра, поперечного метацентрического радиуса и плеча восстанавливающего момента GK для различных углов крена судна. Такой расчет делают начиная от прямого положения через 5— 10° до того угла крена, когда восстанавливающее плечо превращается в нуль и судно приобретает отрицательную остойчивость. По данным этого расчета для наглядного представления об остойчивости судна на больших углах крена строят диаграмму статической остойчивости (ее также называют диаграммой Рида), показывающую зависимость плеча статической остойчивости (GK) или восстанавливающего момента Мвосcт от угла крена 8 (рис. 142). На этой диаграмме по оси абсцисс откладывают углы крена, а по оси ординат — значение восстанавливающих моментов или плечи восстанавливающей пары, так как при равнообъемных наклонениях, при которых водоизмещение судна D остается постоянным, восстанавливающие моменты пропорциональны плечам остойчивости.

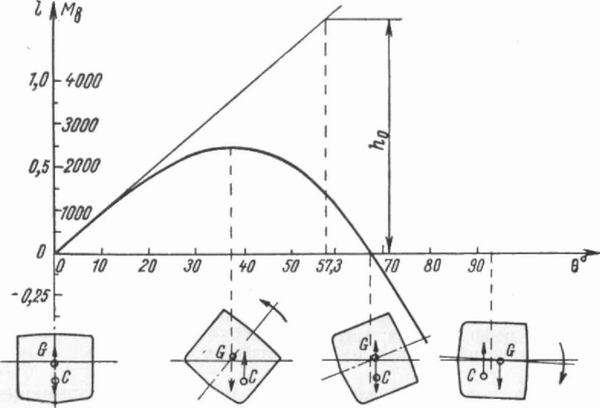
Рис. 142. Диаграмма статической остойчивости.

Диаграмму статической остойчивости строят для каждого характерного случая нагрузки судна, и она следующим образом характеризует остойчивость судна:

1) на всех углах, при которых кривая расположена над осью абсцисс, восстанавливающие плечи и моменты имеют положительное значение, и судно имеет положительную остойчивость. При тех углах крена, когда кривая расположена под осью абсцисс, судно будет неостойчивым;

2) максимум диаграммы определяет предельный угол крена Θ мах и предельный кренящий момент при статическом наклонении судна;

3) угол Θ , при котором нисходящая ветвь кривой пересекает ось абсцисс, называется углом заката диаграммы . При этом угле крена восстанавливающее плечо становится равным нулю;

4) если на оси абсцисс отложить угол, равный 1 радиану (57,3°), и из этой точки восставить перпендикуляр до пересечения с касательной, проведенной к кривой из начала координат, то этот перпендикуляр в масштабе диаграммы будет равен начальной метацентрической высоте h⁰.

Большое влияние на остойчивость оказывают подвижные, т. е. незакрепленные, а также жидкие и сыпучие грузы, имеющие свободную (открытую) поверхность. При наклонении судна эти грузы начинают перемещаться в сторону крена и, как следствие, центр тяжести всего судна уже не будет находиться в неподвижной точке G, а начнет тоже перемещаться в ту же сторону, вызывая уменьшение плеча поперечной остойчивости, что равносильно уменьшению метацентрической высоты со всеми вытекающими из этого последствиями.

Для предотвращения таких случаев все грузы на судах должны быть закреплены, а жидкие или сыпучие должны быть погружены в емкости, исключающие всякое переливание или пересыпание грузов.

При медленном действии сил, создающих кренящий момент, судно, наклоняясь, остановится тогда, когда кренящий и восстанавливающий моменты сравняются.

При внезапном действии внешних сил, таких, как порыв ветра, натяжение буксира на борт, качка, бортовой залп из орудий и т. п., судно, наклоняясь, приобретает угловую скорость и даже с прекращением действия этих сил будет продолжать крениться по инерции на дополнительный угол до тех пор, пока не израсходуется вся его кинетическая энергия (живая сила) вращательного движения судна и его угловая скорость не превратится в нуль.

Такое наклонение судна под действием внезапно приложенных сил называется динамическим наклонением . Если при статическом кренящем моменте судно плавает, имея лишь некоторый крен 0^СТ, то в случае динамического действия того же кренящего момента оно может опрокинуться. При анализе динамической остойчивости для каждого водоизмещения судна строят диаграммы динамической остойчивости, ординаты которых представляют в определенном масштабе площади, образованные кривой моментов статической остойчивости для соответствующих углов крена, т. е. выражают работу восстанавливающей пары при наклонении судна на угол Θ, выраженный в радианах. При вращательном движении, как известно, работа равна произведению момента на угол поворота, выраженный в радианах,

Т¹ = М^kpΘ.

По этой диаграмме все вопросы, связанные с определением динамической остойчивости, можно решить следующим образом (рис. 143). Угол крена при динамически приложенном кренящем моменте можно найти, нанеся на диаграмму в том же масштабе график работы кренящей пары; абсцисса точки пересечения этих двух графиков дает искомый угол 0^ДИН. Если в частном случае крепящий момент имеет постоянное значение, т. е. М^кр = const, то работа будет выражаться

Т² = М^kpΘ.

а график будет иметь вид прямой, проходящей через начало координат. Для того, чтобы построить эту прямую на диаграмме динамической остойчивости, необходимо отложить по оси абсцисс угол, равный радиану, и провести из полученной точки ординату. Отложив на ней в масштабе ординат величину М^кр в виде отрезка Nn (рис. 143), надо провести прямую ON, которая является искомым графиком работы кренящей пары.

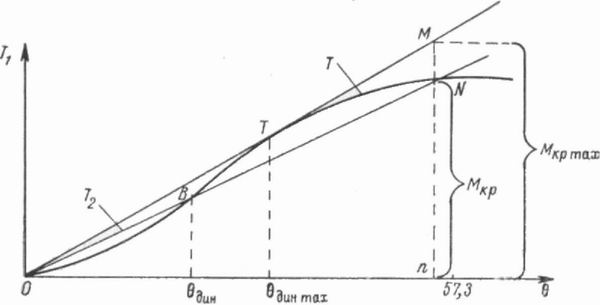
Рис. 143. Определение угла крена и предельного динамического наклонения по диаграмме динамической остойчивости.

На этой же диаграмме показан угол динамического наклонения 0^ДИН, определяемый как абсцисса точки пересечения обоих графиков. С увеличением момента М^кр секущая ON может занять предельное положение, обратившись во внешнюю касательную ОТ, проведенную из начала координат к диаграмме динамической остойчивости. Таким образом, абсцисса точки касания будет искомым предельным углом динамических наклонений Θ Ордината этой касательной, соответствующая радиану, выражает предельный кренящий момент при динамических наклонениях М^крмах. При плавании судно часто подвергается динамическому воздействию внешних сил. Поэтому умение определить динамический кренящий момент при решении вопроса об остойчивости судна имеет большое практическое значение. Изучение причин гибели судов приводит к выводу, что в основном суда гибнут из-за потери остойчивости.

Для ограничения потери остойчивости в соответствии с различными условиями плавания, Регистром разработаны Нормы остойчивости судов транспортного и промыслового флота. В этих нормах основным показателем является способность судна сохранять положительную остойчивость при совместном действии на него бортовой качки и ветра. Судно отвечает основному требованию Норм остойчивости, если при наихудшем варианте загрузки его М^КР остается меньше M^ОПР. При этом минимальный опрокидывающий момент судна определяется по диаграммам статической или динамической остойчивости с учетом влияния свободной поверхности жидких грузов, бортовой качки и элементов расчета парусности судна для различных случаев нагрузки судна. Нормами предусматривается целый ряд требований к остойчивости, например: M^КР < M^ОПР, коэффициент запаса остойчивости

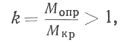
метацентрическая высота должна иметь положительное значение, угол заката диаграммы статической остойчивости должен быть не менее 60°, а с учетом обледенения — не менее 55° и т. п. Обязательное соблюдение этих требований при всех случаях нагрузки дает право считать судно остойчивым.

ДСО позволяет решать многие задачи статики судна, например, определять статический угол крена судна при действии на него постоянного (независящего от крена судна) кренящего момента М_кр = const. Этот угол крена может быть определен из условия равенства кренящего и восстанавливающего моментов М_в (θ) = М_кр. Практически эта задача решается как задача по нахождению абсциссы точки пересечения графиков обоих моментов (Рис.143).

Диаграмма статической остойчивости отражает возможность судна создавать восстанавливающий момент при наклонении судна. Её вид имеет строго конкретный характер, соответствующий параметрам загрузки судна только в данном рейсе (Р = Р_i , h₀ = h_0i). Судоводитель, занимающийся на судне вопросами планирования рейса погрузки и расчетами остойчивости, обязан построить конкретную ДСО для двух состояний судна в предстоящем рейсе: с неизменным первоначальным расположением груза и при 100 % и при 10 % судовых запасов.

Чтобы иметь возможность строить диаграммы статической остойчивости при различных сочетаниях водоизмещения и метацентрической высоты, он пользуется вспомогательными графическими материалами, имеющимися в судовой документации по проекту этого судна, например, пантокаренами, либо универсальной диаграммой статической остойчивости.

ПАНТОКАРЕНЫ.

Пантокарены поставляются на судно проектировщиком в составе информации об остойчивости и прочности для капитана.

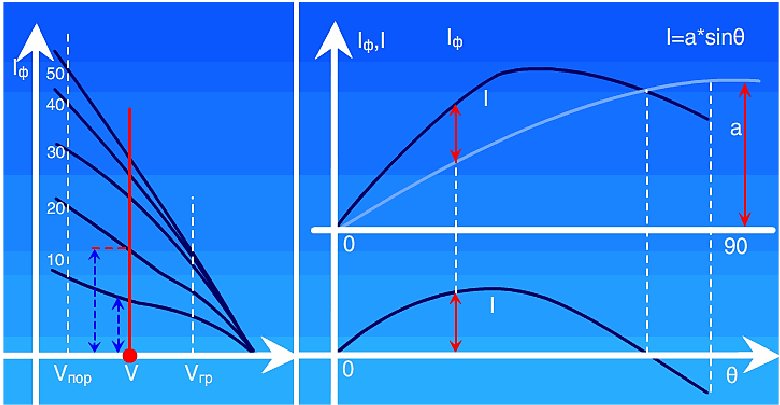
Рис.144: а) пантокарены; б) графики для определения плеч статической остойчивости.

Пантокарены представляют собой универсальные графики для данного судна, отражающие форму его корпуса в части остойчивости.

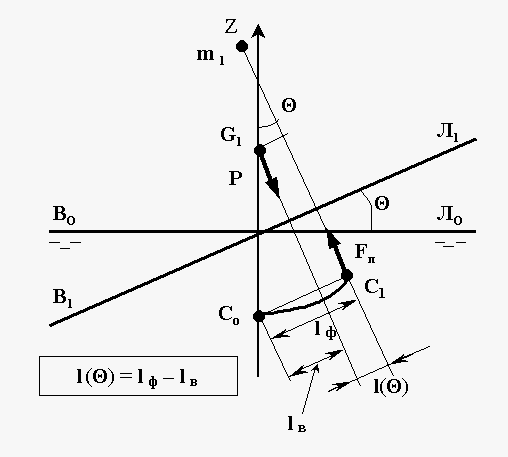
Пантокарены (Рис.144) изображены в виде серии графиков (при разных углах крена ( θ = 10,20,30,….70˚)) в зависимости от веса судна (или его осадки) некоторой части плеча статической остойчивости, называемой плечом остойчивости формы – l_ф (Р, θ).

Плечо формы - это расстояние, на которое переместится сила плавучести относительно исходного центра величины C_ο при крене судна. Понятно, что это смещение центра величины связано только с формой корпуса и не зависит от положения центра тяжести по высоте. Набор значений плеча формы при разных углах крена (при конкретном весе судна Р=Р_i) снимают с графиков пантокарен.

Чтобы определить плечи остойчивости l (θ) и построить диаграмму статической остойчивости в предстоящем рейсе необходимо дополнить плечи формы – плечами веса l_в, которые легко рассчитать (см. Рис. 142):

l_в = (z_G – z_Co) sin θ.

ординаты будущей ДСО получаются по выражению:

l (θ) = l_ф (Р,θ) – l_в (z_G,θ

Рис.145. Плечи остойчивости формы и веса.

Выполнив вычисления для двух состояний нагрузки (Р_зап. = 100% и 10%), строят на чистом бланке две ДСО, характеризующих остойчивость судна в этом рейсе. Остается выполнить проверку параметров остойчивости на их соответствие национальным или международным нормативам по остойчивости морских судов.