Потери энергии при движении потока жидкости по трубе

Потери энергии (напора) принято подразделять на две категории:

· потери энергии распределённые,

· потери энергии сосредоточенные

Распределенные потери энергии – это потери пропорцио­нальные длине трубопровода (канала, русла реки и др.). Называются они потерями энергии по длине. Потери энергии по длине обусловлены внутренним трением (трением между слоями жидкости) и поэтому происходят и в гидравлически гладких и в гидравлически шероховатых трубах.

Сосредоточенные потери энергии – это потери энергии на локальной длине потока (достаточно малой по сравнению с протяжённостью всего потока). Такие потери энергии называют местными потерями или потерями энергии на местных гидравлических сопротивлениях. К местным потерям в гидравлике относят потери на угловых, концевых и переходных соединениях и потери, связанные с изменением сечения трубопроводов, изгибов трубопроводов и т.д.

Потери энергии по длине и потери энергии местные выражаются в виде суммарной потери рабочего давления.

Оценка величины местных потерь и потерь по длине рассчитывается в долях от скоростного напора (кинетической энергии) единицы объема жидкости.

Формула для определения потерь по длине для круглой трубы постоянного сечения длиной l и диаметром d как для ламинарного, так и турбулентного режима одна и та же:

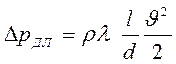(3.8)

где l – коэффициент потерь на трение (иликоэффициент Дарси).

Коэффициент Дарси для ламинарного и турбулентного режимов течения жидкости разный. Эту формулу можно применять для труб любого сечения, но тогда вместо внутреннего диаметра d трубопровода нужно подставить гидравлический радус 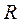потока..

При ламинарном характере течения жидкости для определения коэффициента Дарси можно использовать следующие формулы.

Для гладких труб и шлангов без резких сужений, вмятин и изгибов:

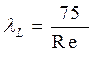(3.9)

· при вмятинах, уменьшающих сечение на 40% … 50%:

;

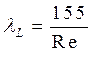· для узких кольцевых концентрических щелей:

;

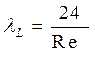· для эксцентричных щелей при максимальном эксцентриситете:

.

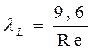При турбулентном характере течения жидкости коэффициент потерь на трение (обозначим его 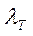) будет значительно больше, чем 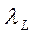, и он существенно зависит от числа Рейнольдса (рис. 3.5).

Наиболее применимыми формулами для определения 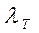являются следующие эмпирические и полуэмпирические зависимости:

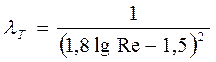, применяемая для чисел Рейнольдса в пределах 2300…несколько миллионов, или

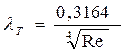,используемая в интервале чисел Рейнольдса 2300… ...100000 (формула Блазиуса).

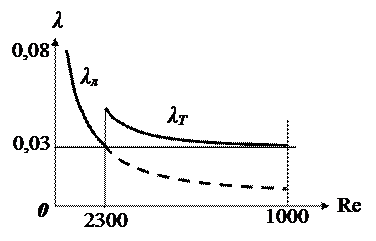
Рис. 3.5.Характер зависимости потерь на трение от числа

Рейнольдса при ламинарном и турбулентном течении жидкости

Местные потери давления при любом режиме течения можно рассчитать по формуле:

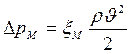, (3.10)

где 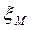– коэффициент местных потерь.

Коэффициент местного сопротивления зависит от конкретных геометрических размеров местного сопротивления и его формы. Значения коэффициентов местных сопротивлений необходимо искать в справочной литературе по гидравлике.

Местные потери можно выразить как через скоростной напор, соответствующий скорости до препятствия в потоке, так и через скоростной напор, подсчитанный по скорости за этим препятствием. Обычно в выше приведенную формулу подставляют среднюю скорость за препятствием. Иногда в справочниках коэффициенты местных потерь даются для скоростного напора до препятствия. Это нужно учитывать при пользовании справочными данными.

Для ламинарного течения по закону Пуазейля можно связать зависимость потерь давления по длине от геометрических размеров трубы и параметров движущейся жидкости:

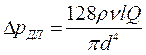
где 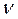– кинематическая вязкость, м²/с;

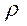– плотность жидкости, кг/м³ ;

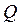– расход жидкости, м³/с;

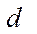– внутренний диаметр трубы, м;

l – длина гладкой трубы.