Класична теорія електропровідності металів

Електричний струм в металах - це впорядкований рух електронів під дією електричного поля. Досліди показують, що при протіканні струму по металевому провідникові не відбувається перенесення речовини, отже, іони металу не беруть участі в перенесенні електричного заряду.

Найбільш переконливий доказ електронної природи струму в металах був отриманий в дослідах з інерцією електронів. Ідея таких дослідів і перші якісні результати належать російським фізикам Л. І. Мандельштаму і Н. Д. Папалескі (1913 р.). У 1916 році американський фізик Р. Толмен і шотландський фізик Б. Стюарт удосконалили методику цих дослідів і виконали кількісні виміри, що неспростовно довели, що струм в металевих провідниках обумовлений рухом електронів.

Схема досліду Толмена і Стюарта показана на рисунку 3.29. Котушка з великим числом витків тонкого дроту приводилася в швидке обертання навколо своєї осі. Кінці котушки за допомогою гнучких дротів були приєднані до чутливого балістичного гальванометра Г. Розкручена котушка різко гальмувалася, і в колі виникав короткочасних струм, обумовлений інерцією носіїв заряду. Повний заряд, що протікає по колу, вимірювався по відхиленню стрілки гальванометра.

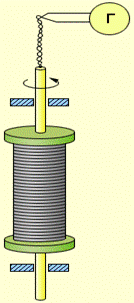
Рисунок 3.29.

Хороша електропровідність металів пояснюється високою концентрацією вільних електронів, що дорівнює по порядку величини числу атомів в одиниці об'єму.

Припущення, що за електричний струм в металах відповідальні електрони, виникло значно раніше за досліди Толмена і Стюарта. Ще в 1900 році німецький учений П. Друде на основі гіпотези про існування вільних електронів в металах створив електронну теорію провідності металів. Ця теорія отримала розвиток в роботах голландського фізика Х. Лоренца і носить назву класичної електронної теорії. Згідно цієї теорії, електрони в металах поводяться як електронний газ, багато в чому схожий на ідеальний газ. Електронний газ заповнює простір між іонами, що утворюють кристалічні грати металу (рис. 3.30).

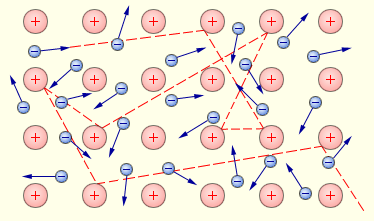
Рисунок 3.30.

Із-за взаємодії з іонами електрони можуть покинути метал, лише здолавши так званий потенціальний бар'єр. Висота цього бар'єру називається роботою виходу. При звичайних (кімнатних) температурах у електронів бракує енергії для подолання потенціального бар'єру.

Як іони, що утворюють кристалічні грати, так і електрони беруть участь в тепловому русі. Іони здійснюють теплові коливання поблизу положень рівноваги - вузлів кристалічної грати. Вільні електрони рухаються хаотично і при своєму русі стикаються з іонами грат. В результаті таких зіткнень встановлюється термодинамічна рівновага між електронним газом і гратами. Згідно теорії Друде-Лоренца, електрони мають таку ж середню енергію теплового руху, як і молекули одноатомного ідеального газу. Це дозволяє оцінити середню швидкість v_т теплового руху електронів по формулах молекулярно-кінетичної теорії. При кімнатній температурі вона виявляється приблизно рівною 10⁵ м/с.

При накладенні зовнішнього електричного поля в металевому провіднику окрім теплового руху електронів виникає їх впорядкований рух (дрейф), тобто електричний струм. Середню швидкість v_ддрейфу можна оцінити з наступних міркувань. За інтервал часу Δt через поперечний переріз S провідника пройдуть усі електрони, що знаходилися в об'ємі Sv_д Δt

Число таких електронів рівне nSv_д Δt, де n - середня концентрація вільних електронів, приблизно рівна числу атомів в одиниці об'єму металевого провідника. Через переріз провідника за час Δt пройде заряд Δq=enSv_дΔt Так як:

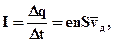тоді

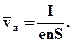
Концентрація n атомів в металах знаходиться в межах 10²⁸-10²⁹ м^-3.

Оцінка по цій формулі середньої швидкостіv_д впорядкованого руху електронів, для металевого провідника перерізом 1 мм², по якому тече струм 10 А, дає для значення в межах 0,6-6 мм/c. Таким чином, середня швидкість v_д впорядкованого руху електронів в металевих провідниках на багато порядків менше середньої швидкості v_т їх теплового руху Рисунок 3.31 дає уявлення про характер руху вільного електрона в кристалічній граті.

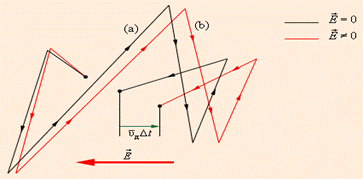
Рисунок 3.31.

Мала швидкість дрейфу не суперечить дослідному факту, що струм в колі постійного струму встановлюється практично миттєво. Замикання кола викликає поширення електричного поля із швидкістю c = 3·10⁸ м/с. Через час порядку l/с (l - довжина кола) уздовж кола встановлюється стаціонарний розподіл електричного поля і в ній починається впорядкований рух електронів.

У класичній електронній теорії металів передбачається, що рух електронів підпорядковується законам механіки Ньютона. У цій теорії нехтують взаємодією електронів між собою, а їх взаємодію з позитивними іонами зводять тільки до зіткнень. Передбачається також, що при кожному зіткненні електрон передає гратам усю накопичену в електричному полі енергію і тому після зіткнення він починає рух з нульовою дрейфовою швидкістю.

Не дивлячись на усі ці допущення, класична електронна теорія якісно пояснює закони електричного струму в металевих провідниках.

Закон Ома

У проміжку між зіткненнями на електрон діє сила, рівна по модулю eE, внаслідок чого він набуває прискорення а. Тому до кінця вільного пробігу дрейфова швидкість електрона становить:

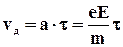
де τ - час вільного пробігу, який для спрощення розрахунків передбачається однаковим для усіх електронів.

Середнє значення швидкості дрейфу дорівнює половині її максимального значення:

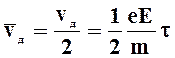
Розглянемо провідник довжини l і перерізом S з концентрацією електронів n. Струм в провіднику може бути записаний у виді:

.

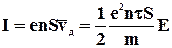Так. як 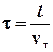,де l - середня довжина вільного пробігу електронів, а v_т середня швидкість теплового руху електронів густина струму дорівнює:

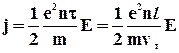. (3. 45)

Отримана формула виражає закон Ома для металевого провідника. Коефіцієнт пропорційності між J і E не що інше, як питома провідність матеріалу провідника.

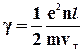. (3. 46)