Принцип суперпозиції електричного поля.
Якщо електричне поле створюється декількома зарядами, то напруженість результуючого поля в цій точці визначається векторною сумою напруженостей кожного заряду.
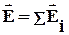 .
.
 На рисунку 3.5 показана напруженість результуючого поля двох точкових зарядів q1 і q2в точці О.
На рисунку 3.5 показана напруженість результуючого поля двох точкових зарядів q1 і q2в точці О.
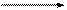
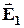


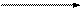
 О
О 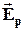
 q1
q1 
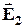
 q2
q2
Рисунок 3.5.
 У тому випадку, коли заряджене тіло не можна вважати точковим, формулу напруженості електричного поля треба записувати в диференціальному виді.
У тому випадку, коли заряджене тіло не можна вважати точковим, формулу напруженості електричного поля треба записувати в диференціальному виді.
. (3.5)
де dE - елементарна напруженість електричного поля елементарного заряду dq.
Приклад розв’язку задачі :
Розрахувати напруженість електричного поля в точці, віддаленій на 1 см від центру рівномірно зарядженого тонкого стержня завдовжки 1 м Заряд стержня дорівнює
1 нКл.
Розв’язок.
 В даному випадку заряджене тіло не можна вважати точковим зарядом, тому для вирозв’язку задачі поступимо таким чином. Заряджений стержень подумки розіб'ємо на нескінченно малі ділянки завдовжки dl, кожна ділянка стержня містить заряд dq і в точці О електричного поля створює напруженість
В даному випадку заряджене тіло не можна вважати точковим зарядом, тому для вирозв’язку задачі поступимо таким чином. Заряджений стержень подумки розіб'ємо на нескінченно малі ділянки завдовжки dl, кожна ділянка стержня містить заряд dq і в точці О електричного поля створює напруженість
Dq dl


 r r0
r r0

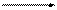
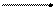

 О
О





 Результуюча напруженість дорівнює векторній сумі елементарних напряженностей . Якщо вектор розкласти на два складових вектори то в результаті інтегруванняї , так,. як сума усіх складових через симетрію дорівнює 0. Тоді вектор напруженості результуючого поля в точці О буде спрямований так само як , а його модуль рівний
Результуюча напруженість дорівнює векторній сумі елементарних напряженностей . Якщо вектор розкласти на два складових вектори то в результаті інтегруванняї , так,. як сума усіх складових через симетрію дорівнює 0. Тоді вектор напруженості результуючого поля в точці О буде спрямований так само як , а його модуль рівний


 Далі необхідно перетворити вираз щоб прийти до однієї змінної інтегрування. Введемо поняття лінійної густини заряду тоді dq=τdl,
Далі необхідно перетворити вираз щоб прийти до однієї змінної інтегрування. Введемо поняття лінійної густини заряду тоді dq=τdl,

 ,
,
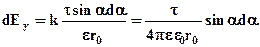
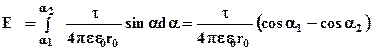
Так, як довжина стержня l набагато більша відстані r0 α1 прагне до нуля, α2 прагне до 180°.
 .
.

Тоді .
У розрахунках було прийнято, що заряджене тіло знаходилося у вакуумі (чи повітрі) ε=1
Дата добавления: 2020-10-25; просмотров: 595;











