Influence of bar end conditions on the critical force
Usually the bar ends are fixed by one of four ways shown in Fig. 9.4. The pin-ended bar is the second way considered earlier, when Euler’s formula was drawn.
Under other ways of the bar end condition generalization Euler’s formula for determining the critical load looks like this:
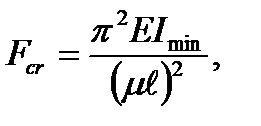 (9.7)
(9.7)
where μ is the coefficient of the effective bar length dependent on the way of the bar end fixation, 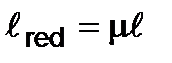 - the effective bar length.
- the effective bar length.
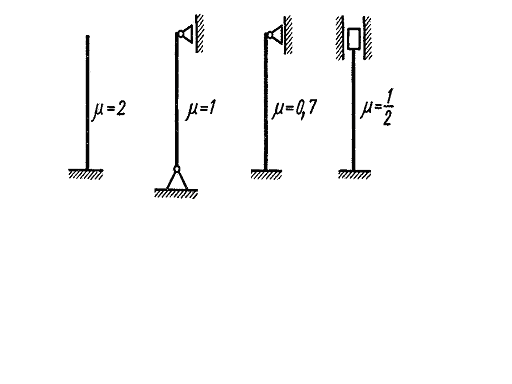
Fig. 9.4.
Formula (9.7) is obtained if we consider the differential equation of the elastic buckling
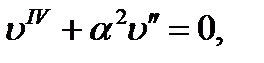
The equation in question follows from the equation by double differentiating.
Solving of this equation is
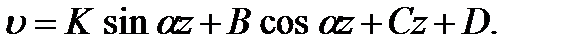
The constants K, B, C, D are determined from the boundary conditions. For example, for the third case of fixation (Fig. 9.4) at the coordinate origin on the lower end we have (  - is the bar length):
- is the bar length):
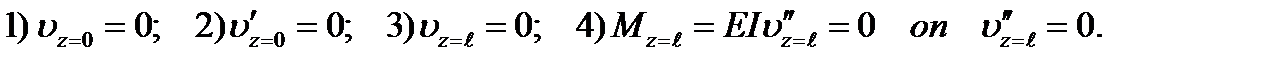
Using these conditions we get
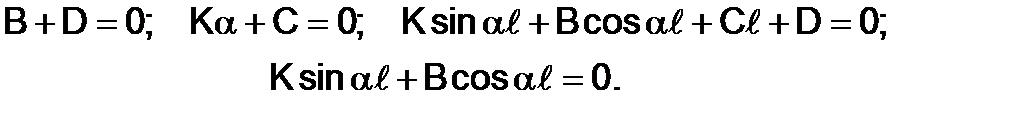
It is known from mathematics that the homogeneous equations system (i.e. without free members) has a non-equal to zero solving only when its determinant is equal to zero:
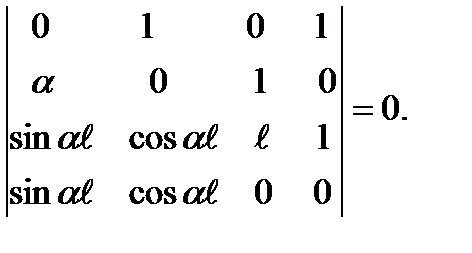
Expanding this determinant we get 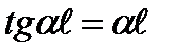 . The minimum root of this equation is not equal to zero,
. The minimum root of this equation is not equal to zero, 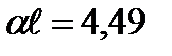 then
then
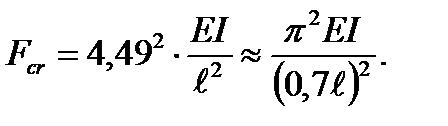
Thus 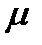 = 0,7.
= 0,7.
Analogously the coefficient values pointed in Fig. 9.4 are got under other ways of the bar end fixation.
As it can be seen from the formula (9.7) the lesser μ is – the larger is the critical, thus, the allowable bar load. For example, the bar load clamped by both ends can be in sixteen times larger than the bar load clamped by one end. Therefore, both bar ends should be clamped rigidly where it is possible. Although, it is not always possible in practice. Elements to which the bar ends are clamped are always more or less elastic, maileable, which introduces some indeterminateness for the design. So very often even under rididly clamped bar ends with other elements the design is done in the factor of stability supposing pinning at both bar ends.
9.4. Applicability limits of of Euler’s formula
Euler’s formula cannot always be used. When deriving it we used a differential equation of the elastic line based on Hooke’s law. Hooke’s law as it is known is true until the stresses do not surpass the proportional limit. To establish the limits of applicability of Euler’s formula let us determine the critical stress 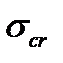 i.e. the stress arising at the bar cross section under the action of the critical load:
i.e. the stress arising at the bar cross section under the action of the critical load:
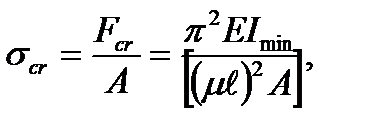 (9.8)
(9.8)
where A is a section of the bar cross area.
But 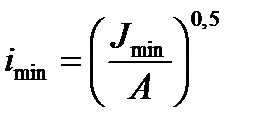 - is the minimum radius of the bar cross section gyration. Therefore the formula (9.8) can be written in the form
- is the minimum radius of the bar cross section gyration. Therefore the formula (9.8) can be written in the form
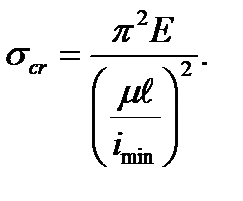
The value 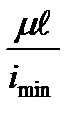 characterizes the influence of the bar dimensions and the fixation way of the ends; it is called the slenderness ratio and denoted by
characterizes the influence of the bar dimensions and the fixation way of the ends; it is called the slenderness ratio and denoted by 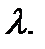 The slenderness ratio is the dimensionless value.
The slenderness ratio is the dimensionless value.
Thus, denoting 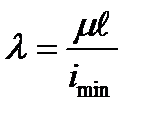 we get
we get
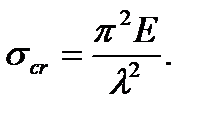
To be able to use Euler’s formula the following condition must be satisfied:
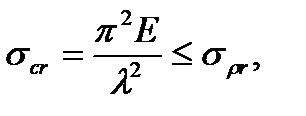 (9.9)
(9.9)
where 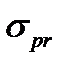 is the proportional limit of the bar material.
is the proportional limit of the bar material.
Writing down the formula (9.9) concerning slenderness we get the condition of Euler’s formula application in the form
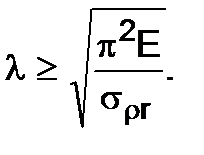 (9.10)
(9.10)
For example, for steel Ст. 3 we have 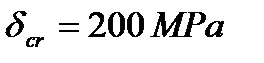 and
and
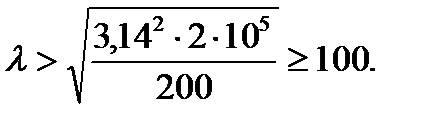
Thus, for the bars from the low-carbon steel Euler’s formula is applied if their slenderness is more than 100.
Analogously, we get the conditions of Euler’s formula application for cast-iron, i.e. 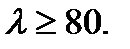 For medium-carbon and high-carbon and also for alloy steels Euler’s formula is applied under slenderness lesser than pointed. So, for bars from chrome-molybdenum steel Euler’s formula is applied at
For medium-carbon and high-carbon and also for alloy steels Euler’s formula is applied under slenderness lesser than pointed. So, for bars from chrome-molybdenum steel Euler’s formula is applied at 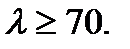
Дата добавления: 2020-10-25; просмотров: 634;











