Вычисление напряжений при равноускоренном движении

Во многих случаях ускорения, с которыми перемещаются детали машин, известны. Динамические напряжения в этих случаях вычисляются без затруднений.

Рассмотрим несколько примеров.

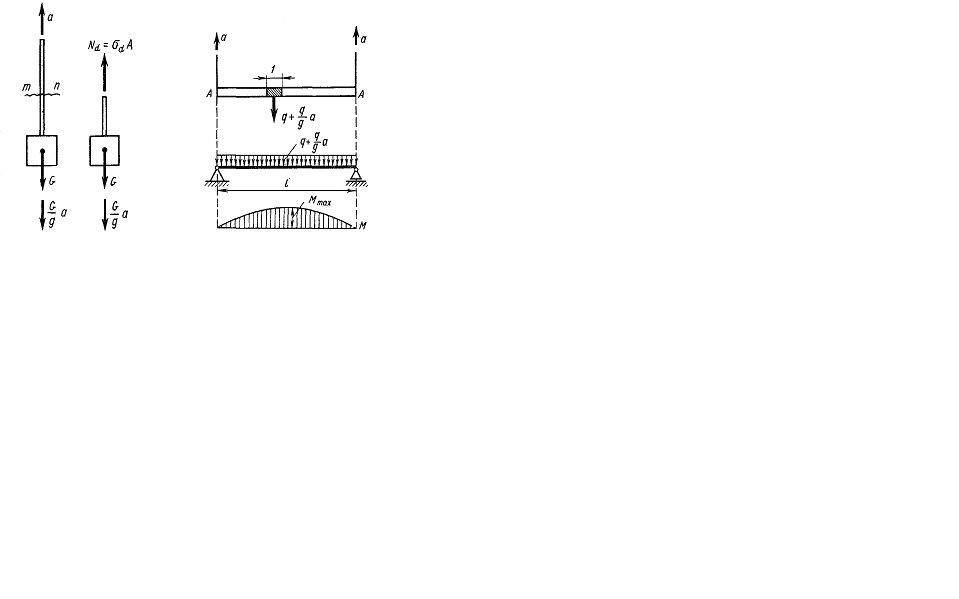
Рис. 10.1. Рис. 10.2.

Рис. 10.1. Рис. 10.2.

Пример 1. Груз весом G поднимают вверх с ускорением (рис. 10.1). Определить напряжение в канате, пренебрегая его весом.

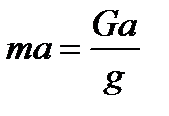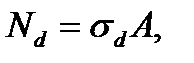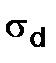Решение. Прикладываем к грузу силу инерции, равную и направленную вниз. Применим метод сечений. Делаем разрез п - п и отбрасываем верхнюю часть каната. Усилие в канате обозначаем N_d, так как напряжения при центральном растяжении равномерно распределены по сечению, то можем принять, что где - искомое динамическое напряжение в канате.

Проецируя все силы, в том числе и силы инерции, на вертикальную ось, получаем

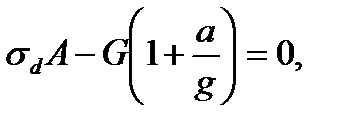(10.1)

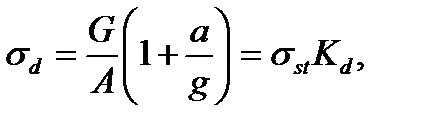(10.2)

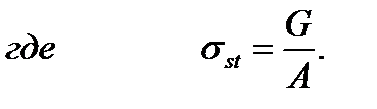
напряжение при статическом действии груза. 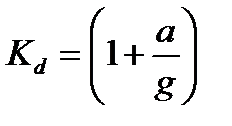1 - динамический коэффициент.

Таким образом, динамические напряжения во многих случаях могут быть выражены через статические напряжения и динамический коэффициент. Это особенно удобно, так как динамический коэффициент часто приходится определять опытным путем.

Пример 2. Стержень, вес 1 м длины которого равен q, поднимают; с помощью двух нитей, привязанных к его концам (рис. 10.2). Движение поступательное с ускорением а. Определить напряжения в стержне.

Решение. Прикладываем к каждому элементу стержня длиной, равной единице, силу инерции 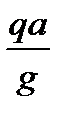. Видим, что эта задача эквивалентна задаче о простой балке, нагруженной равномерно распределенной нагрузкой интенсивностью .

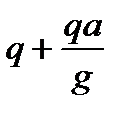Наибольший изгибающий момент будет в сечении посередине балки:

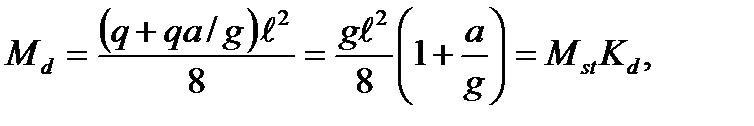(10.3)

где 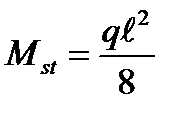-изгибающий момент от статической равномерно распределенной нагрузки интенсивностью q; -динамический коэффициент.

Наибольшее динамическое напряжение определяется по обычной формуле изгиба

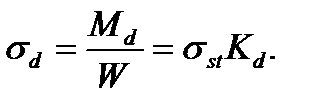(10.4)