Кручение с растяжением (сжатием)

В этом случае в поперечных сечениях стержня возникают одновременно два внутренних усилия: крутящий момент и продольная сила (растягивающая или сжимающая).

Для стержня круглого сечения наибольшие касательные напряжения при кручении имеют место в точках контура сечения 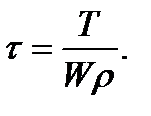При растяжении во всех точках поперечного сечения возникают нормальные напряжения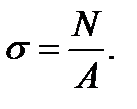

Теперь, так же как и в случае кручения с изгибом, следует определить главные напряжения и применить соответствующую гипотезу прочности. В результате получим для эквивалентных напряжений формулу (7.29) (по третьей гипотезе прочности) или (7.34) (по четвертой гипотезе). В эти формулы следует подставить значения 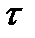и , приведенные выше.

Окончательно получим условие прочности для кручения с растяжением (сжатием):

а) по третьей гипотезе прочности,

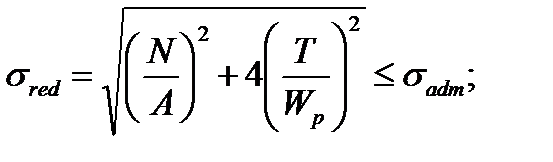(7.37)

б) по четвертой гипотезе прочности,

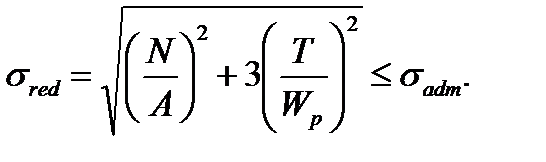(7.38)

Рекомендуется отдавать предпочтение формуле (7.38), так как четвертая гипотеза для пластичных материалов хорошо согласуется с опытными данными и приводит к более экономичным решениям.