Изгиб в двух плоскостях (косой изгиб)

Косой изгиб возникает в том случае, когда внешние силы, перпендикулярные оси стержня, не лежат в плоскости, проходящей через главную ось его поперечного сечения (рис. 7.1). В этом случае возникающий в поперечном сечении изгибающий момент можно разложить на два изгибающих момента, действующих в плоскостях, проходящих через главные оси сечения. Таким образом, косой изгиб можно рассматривать как сочетание двух плоских изгибов во взаимно перпендикулярных плоскостях.

При косом изгибе нормальные напряжения в любой точке поперечного сечения будут равны алгебраической сумме напряжений от изгиба в обеих плоскостях.

Рассмотрим, например, точку С опорного сечения, имеющую координаты х и у, относительно главных осей.

В этом сечении:

а) изгибающий момент, возникающий при изгибе стержня в вертикальной плоскости с нейтральной осью х,

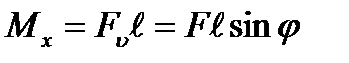(7.1)

б) изгибающий момент, возникающий при изгибе стержня в горизонтальной плоскости с нейтральной осью у,

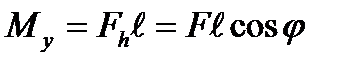(7.2)

Здесь F_u и F_h - вертикальная и горизонтальная составляющие силы F; 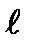- длина балки; 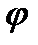- угол наклона силовой плоскости относительно оси х.

При изгибе в вертикальной плоскости в верхней половине балки (в том числе и в точке С) возникают растягивающие напряжения, в нижней половине балки - сжимающие, так как выпуклая сторона балки будет наверху. Напряжения в точке С определяем по следующей формуле, уже известной из теории плоского изгиба:

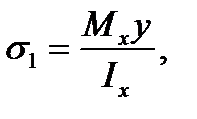(7.3)

где у - расстояние от нейтральной оси х до точки С; 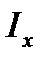- момент инерции поперечного сечения балки относительно оси х.

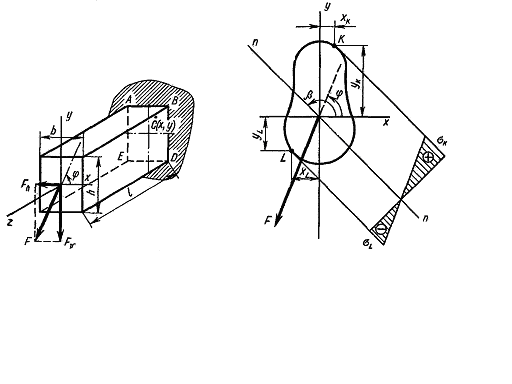
Рис. 7.1. Рис. 7.2.

Вследствие изгиба в горизонтальной плоскости в правой половине балки, а следовательно, и в точке С возникают растягивающие напряжения, а в левой половине балки - сжимающие, так как выпуклая сторона балки при изгибе в горизонтальной плоскости будет справа. В этом легко убедиться, изогнув гибкую линейку в горизонтальной плоскости. Напряжения в точке С при этом будут определяться по аналогичной формуле

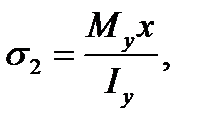(7.4)

где х - расстояние от оси у (нейтральной оси при изгибе в горизонтальной плоскости) до точки С; 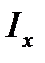- момент инерции поперечного сечения балки относительно оси у. Суммарное напряжение в точке С

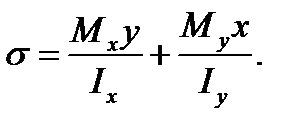(7.5)

Эта формула справедлива и при любой другой форме сечения балки. Если сечение имеет выступающие угловые точки, для которых X_max и У_max достигаются одновременно (прямоугольник, двутавр), то наибольшие по значению напряжения возникают в этих точках:

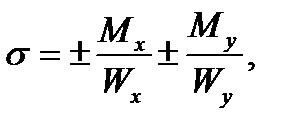(7.6)

где 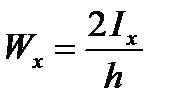- момент сопротивления сечения относительно оси х; 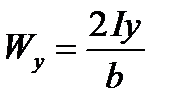- момент сопротивления сечения относительно оси у.

Очевидно, что опасными будут те угловые точки сечения, где суммируются напряжения одного знака.

Для случая, изображенного на рис. 7.1, такими точками будут точки В и Е, при этом точка В находится в растянутой зоне, а точка Е - в сжатой. Поэтому напряжения в точках В и Е равны:

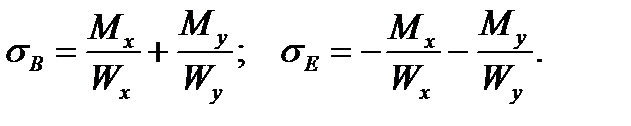(7.7)

Для сечения произвольного очертания, не имеющего выступающих угловых точек, необходимо предварительно найти «опасные» точки, т. е. те точки сечения, в которых будут действовать наибольшие растягивающие и сжимающие напряжения (рис. 7.2).

Это производится следующим образом. Вначале определяется положениенулевой линии при косом изгибе, т. е. определяется геометрическое место точек сечения, в которых нормальные напряжения равны нулю. Другими словами, определяется линия, разделяющая растянутую и сжатую части сечения. Пусть это будет линия пп.

При изгибе напряжения возрастают по мере удаления от нулевой линии.

Это видно из того, что уравнение (7.5) представляет собой уравнение плоскости, проходящей через нулевую линию. Ордината, замеренная по нормали от поперечного сечения до этой плоскости, численно равна напряжению в данной точке. Она будет наибольшей для той точки, которая дальше всех отстоит от нулевой линии.

Учитывая это, заключаем, что точками, в которых следует проверять напряжения, будут точки, наиболее удаленные от нулевой линии, т. е. точки К и L. Для материала, одинаково работающем на растяжение и сжатие, опасной является та из указанных точек, в которой возникает большее (по модулю) напряжение.

Уравнение нулевой линии получим, приравняв левую часть формулы (7.5) нулю:

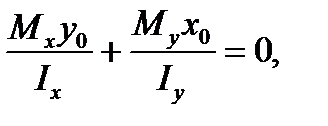(7.8)

или

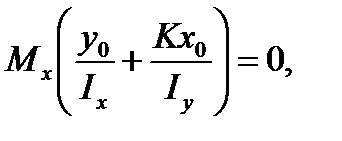(7.9)

где в соответствии с формулами (7.8) и (7.9)

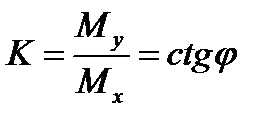(7.10)

a x₀ и y₀ - текущие координаты точек нулевой линии. Так как M_x ≠ 0, то

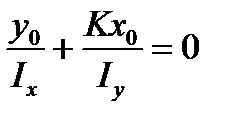(7.11)